Содержание
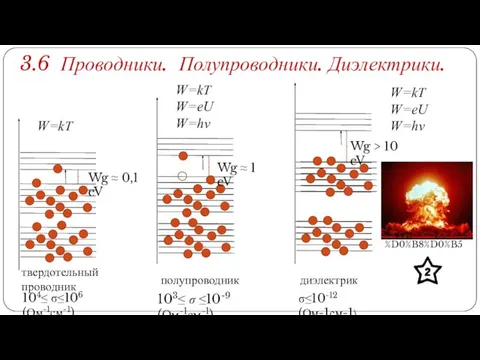
- 2. https://ru.wikipedia.org/wiki/%D0%AF%D0%B4%D0%B5%D1%80%D0%BD%D0%BE%D0%B5_%D0%BE%D1%80%D1%83%D0%B6%D0%B8%D0%B5 твердотельный проводник полупроводник диэлектрик W=kT Wg ≈ 0,1 eV Wg ≈ 1 eV Wg >
- 3. МЕТАЛЛ ПОЛУПРОВОДНИК ДИЭЛЕКТРИК Зона проводимости – Зона свободных электронов Валентная зона Энергии внутренних электронов Валентная зона
- 4. 3.7 Электрическое поле в проводнике Диэлектрик Проводник Зарядим проводящее тело На поверхности диэлектрика, окружающего проводник выделим
- 5. 3.7 Электрическое поле в проводнике Следует помнить, что в электростатике поверхность любого проводника, а следовательно, и
- 6. https://24hitech.ru/kak-sdelat-generator-van-de-graafa-svoimi-rykami.html 3.7 Электрическое поле в проводнике Индукционная машина Электростатическая защита - экранирование Генератор Ван де Граафа
- 7. 3.8 Электрическое поле в диэлектрике Типы диэлектриков полярные неполярные кристаллические Обладают дипольным моментом и в отсутствие
- 8. 3.8 Электрическое поле в диэлектрике Типы диэлектриков полярные неполярные кристаллические Дополнить примерами
- 9. 3.8.1 Кристаллические диэлектрики
- 10. 3.8.1 Кристаллические диэлектрики κ = диэлектрическая восприимчивость
- 11. 3.8.1 Кристаллические диэлектрики Сигнетоэлектричество Пьезоэлектричество Обратный пьезоэлектрический эффект
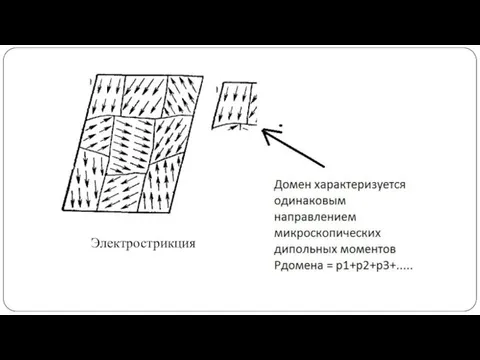
- 12. Электрострикция
- 13. 3.8.1 Кристаллические диэлектрики Пироэлектричество
- 14. 3.9 Поле в неоднородной среде и на границах раздела диэлектриков Поле плоскопараллельной пластины
- 15. 3.9 Поле в неоднородной среде и на границах раздела диэлектриков Поле тела произвольной формы На элементарной
- 16. 3.9 Поле в неоднородной среде и на границах раздела диэлектриков На расстояниях малых от поверхности, можно
- 17. 3.9 Поле в неоднородной среде и на границах раздела диэлектриков
- 18. Ранее мы предполагали, что линии поля и направление вектора поляризации к границе раздела перпендикулярны. В общем
- 19. 3.9 Поле в неоднородной среде и на границах раздела диэлектриков Дополнительное поле, создаваемое этими зарядами, перпендикулярно
- 20. На рисунке изображен случай . При этом и линии вектора E при переходе через границу раздела
- 21. 3.9 Поле в неоднородной среде и на границах раздела диэлектриков Линии индукции преломляются в данном случае
- 22. 3.10 Электрическая емкость проводников
- 23. То есть потенциал в каждой точке возрастает прямо пропорционально заряду проводника. Это утверждение конечно справедливо и
- 24. Откуда следует определение единицы измерения электрической емкости: Электроемкость проводника численно равна величине заряда, который нужно сообщать
- 25. 3.11 Энергия электрического поля
- 27. Скачать презентацию






















 Ремонт муфты сцепления
Ремонт муфты сцепления Электрический ток в газах
Электрический ток в газах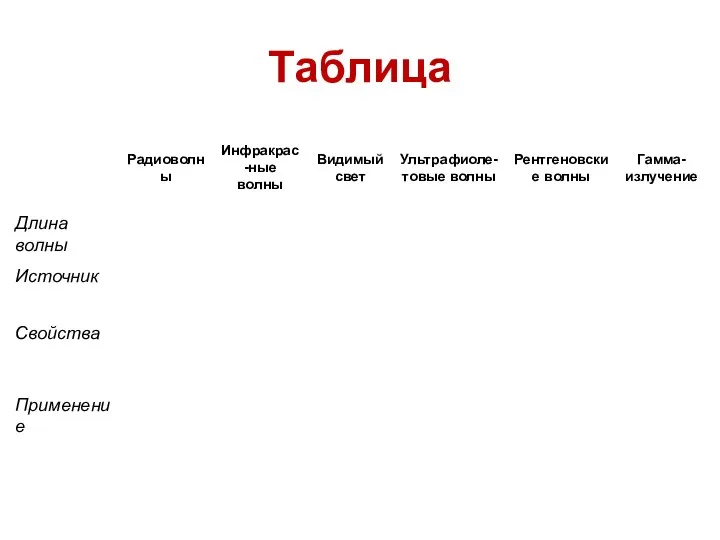 Радиоволны. Таблица. 9 класс
Радиоволны. Таблица. 9 класс Тема урока: Электрическое сопротивление Открываем новое свойство тел!
Тема урока: Электрическое сопротивление Открываем новое свойство тел! Выполнение подготовки центробежного нагнетателя к ремонту
Выполнение подготовки центробежного нагнетателя к ремонту тех мех. 2
тех мех. 2 Презентация на тему Постоянные магниты Магнитное поле Земли
Презентация на тему Постоянные магниты Магнитное поле Земли  Возможности применения кремния как горючего в пиротехнических составах
Возможности применения кремния как горючего в пиротехнических составах Решение задач по кинематики
Решение задач по кинематики Источники звука. Звуковые колебания
Источники звука. Звуковые колебания Презентация на тему Образование природных явлений
Презентация на тему Образование природных явлений  Изменение импульса механической системы
Изменение импульса механической системы Атомно-абсорбционные методы. АSS
Атомно-абсорбционные методы. АSS Кинематика
Кинематика Механические колебания и волны. Решение задач
Механические колебания и волны. Решение задач Свободное падение тел
Свободное падение тел Презентация на тему Вакуумные приборы
Презентация на тему Вакуумные приборы  Основные положения МКТ
Основные положения МКТ Путешествие в страну Физика
Путешествие в страну Физика Испарение и конденсация. Насыщенный и ненасыщенный пар
Испарение и конденсация. Насыщенный и ненасыщенный пар Розв'язування задач. Урок 53. 9 класс
Розв'язування задач. Урок 53. 9 класс Техническое обслуживание буксового узла
Техническое обслуживание буксового узла Сила упругости. Закон Гука. Жесткость
Сила упругости. Закон Гука. Жесткость Тест по теме Электромагнетизм
Тест по теме Электромагнетизм Газовые законы
Газовые законы Значение режима смазывания для увеличения долговечности работы машин и механизмов
Значение режима смазывания для увеличения долговечности работы машин и механизмов Трехфазные электрические цепи
Трехфазные электрические цепи Взаимное притяжение и отталкивание молекул
Взаимное притяжение и отталкивание молекул