Содержание
- 2. Понятие о поверхностях и телах вращения. Представим себе, что плоский многоугольник АВСDE вращается вокруг прямой АВ.
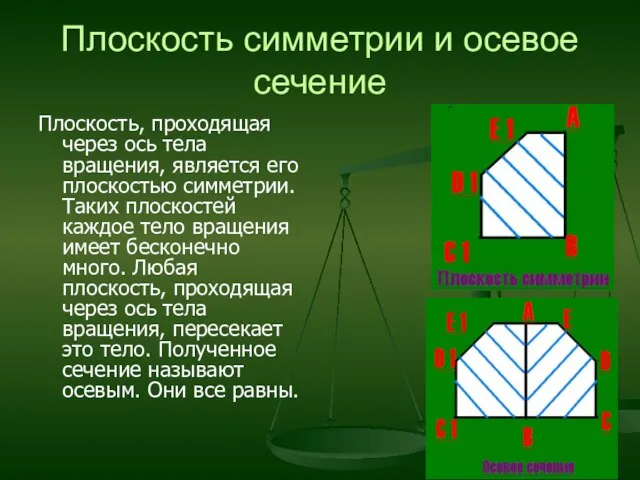
- 3. Плоскость симметрии и осевое сечение Плоскость, проходящая через ось тела вращения, является его плоскостью симметрии. Таких
- 4. Как задать тело вращения: Чтобы задать тело вращения, достаточно указать его ось и фигуру, вращением которой
- 5. Цилиндр
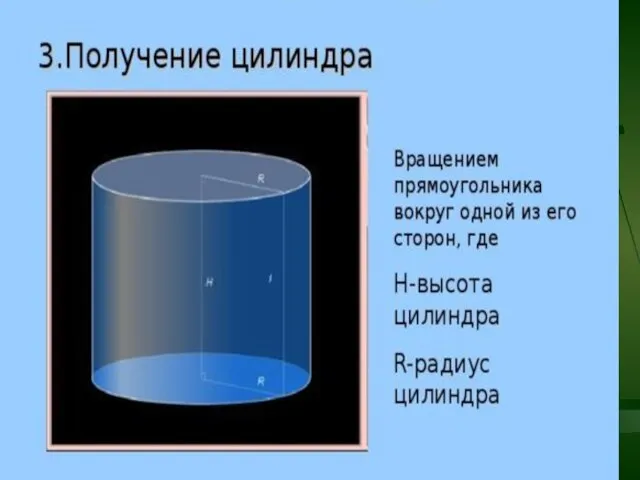
- 8. Определение цилиндра: Цилиндр – это тело, которое состоит из двух кругов, совмещаемых параллельным переносом, и всех
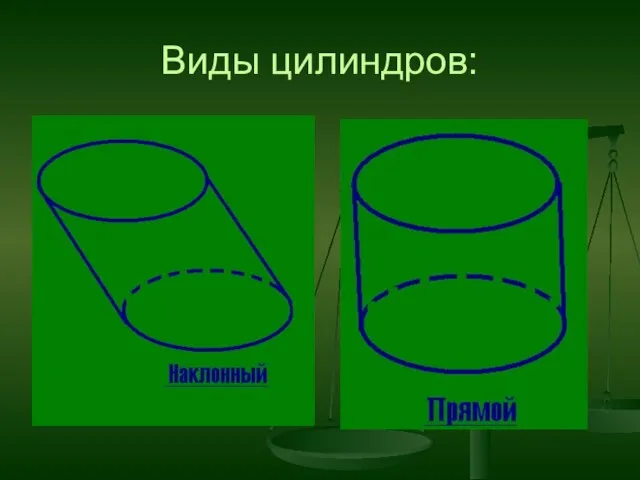
- 9. Виды цилиндров:
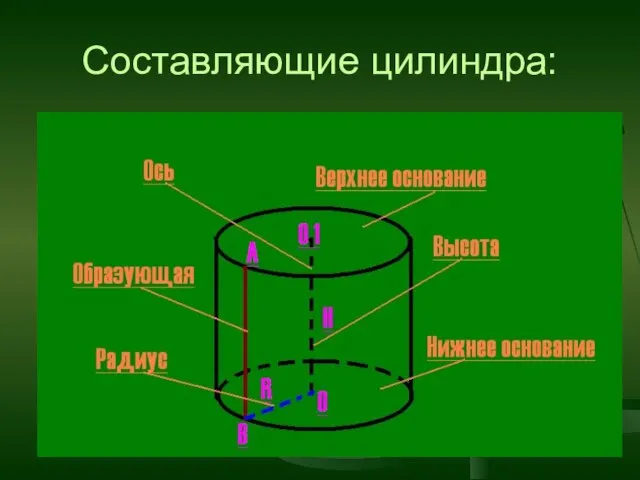
- 10. Составляющие цилиндра:
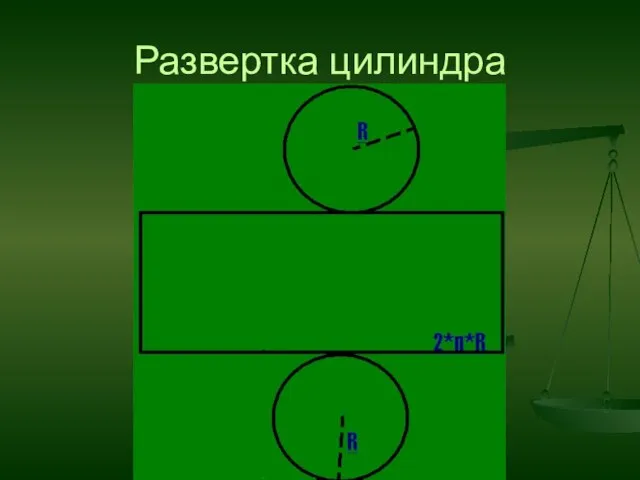
- 11. Развертка цилиндра
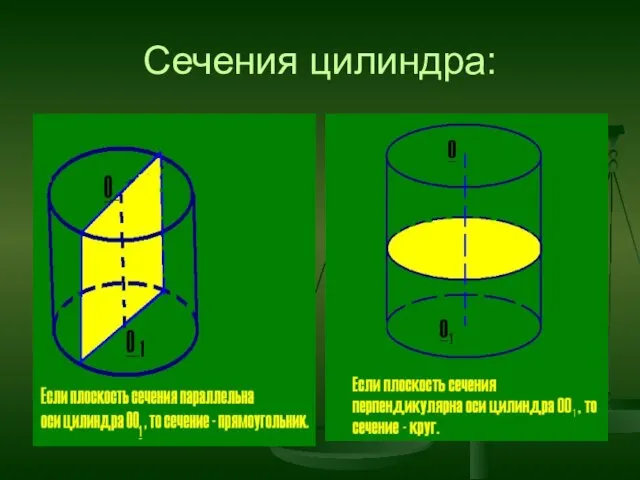
- 12. Сечения цилиндра:
- 13. Основные формулы: Sоснов= пR2 Sбок =2пRH Sполн = 2пR2+2пRH V= Sоснов* H = пR2 H
- 14. Задача: высота цилиндра равна 12 см, а радиус основания – 10 см. Найти площадь боковой поверхности.
- 15. Конус
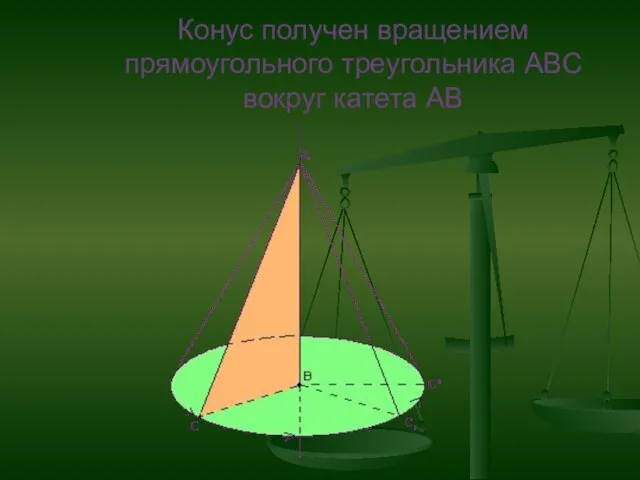
- 16. Конус получен вращением прямоугольного треугольника АВС вокруг катета АВ
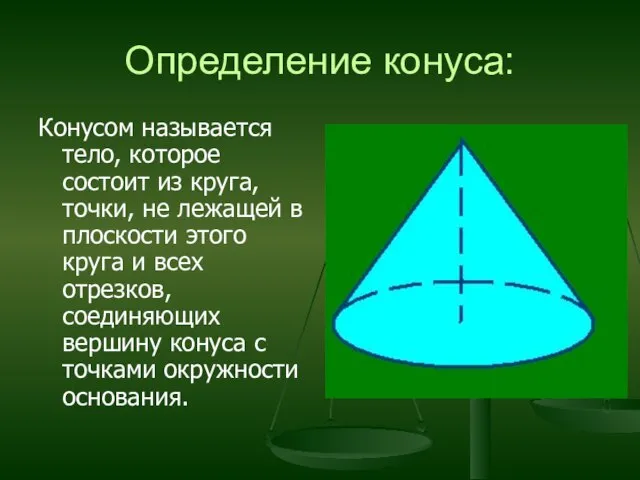
- 17. Определение конуса: Конусом называется тело, которое состоит из круга, точки, не лежащей в плоскости этого круга
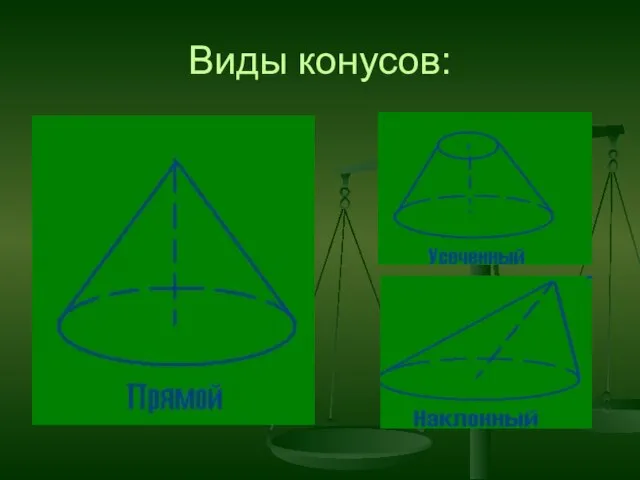
- 18. Виды конусов:
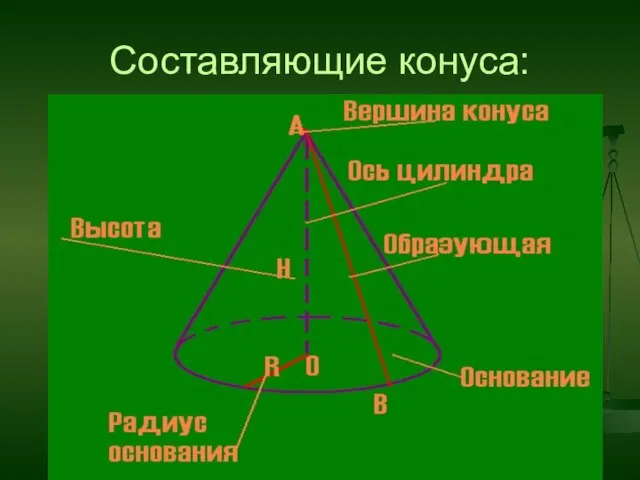
- 19. Составляющие конуса:
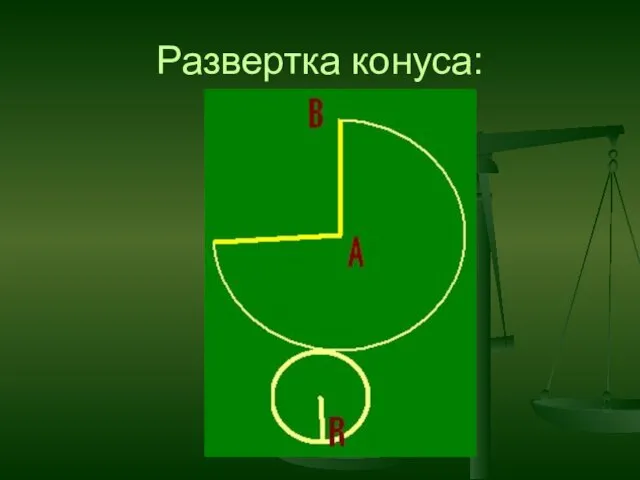
- 20. Развертка конуса:
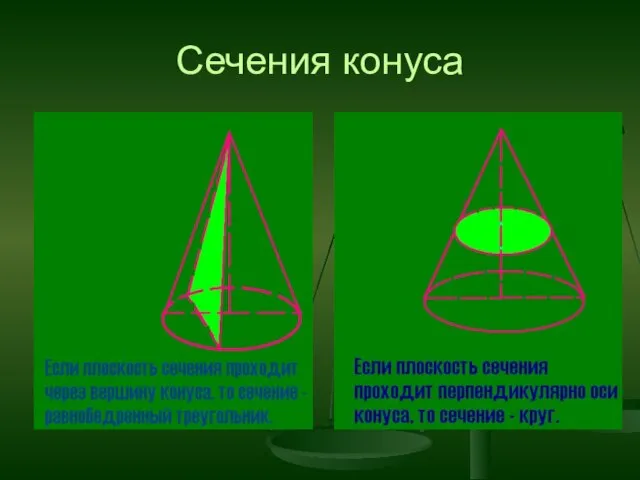
- 21. Осевое сечение конуса. Осевое сечение – это сечение плоскостью, проходящей через ось конуса. Сечение представляет собой
- 22. Сечения конуса
- 23. Определение усеченного конуса: Усеченным конусом называется тело вращения, образованное вращением прямоугольной трапеции около боковой стороны, перпендикулярной
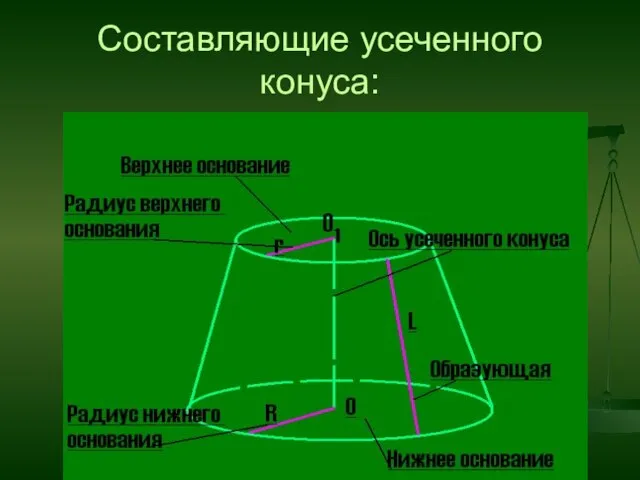
- 24. Составляющие усеченного конуса:
- 25. Основные формулы: Конус: Sбок = пRL Sполн= пR(L+R) V=1/3пR2H Усеченный конус: Sбок = п(R+r)L
- 26. Задача: высота конуса = 15 см, а радиус основания – 8 см. Найти образующую конуса. Решение:
- 27. Шар
- 28. Определение шара: Сфера – поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной
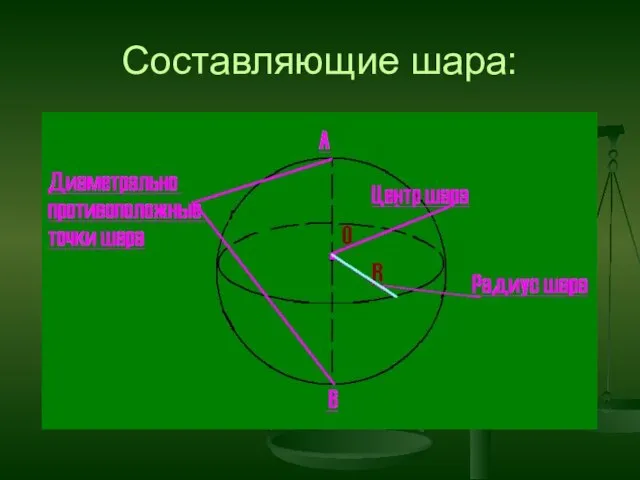
- 29. Составляющие шара:
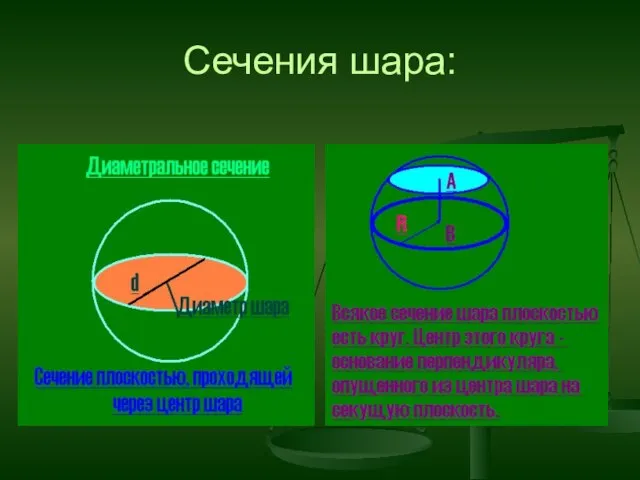
- 30. Сечения шара:
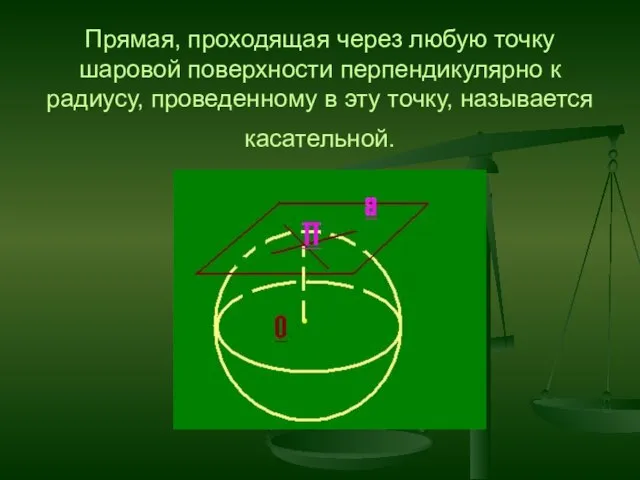
- 31. Прямая, проходящая через любую точку шаровой поверхности перпендикулярно к радиусу, проведенному в эту точку, называется касательной.
- 32. Шаровой сегмент – часть шара, отсекаемая от него плоскостью. Шаровой слой – часть шара, расположенная между
- 33. Основные формулы: Шар: Sполн = 4пR2 V = 4/3пR3 Шаровой сегмент: V = пН2(R –1/3H) Sполн
- 34. Задача: дан шар, радиус которого равен 25 см, найти площадь полной поверхности шара. Решение: используя формулу
- 36. Скачать презентацию

















 Электрокинетические явления
Электрокинетические явления Теоретический чертеж. Координатные оси
Теоретический чертеж. Координатные оси Основные понятия, определения и законы электромеханики
Основные понятия, определения и законы электромеханики Телескопи. Типи телескопів за розташуванням
Телескопи. Типи телескопів за розташуванням M_P_Rezistivnye_M (1)
M_P_Rezistivnye_M (1) Презентация Механика Лекция 1
Презентация Механика Лекция 1 Резистор. Функциональное назначение резистра
Резистор. Функциональное назначение резистра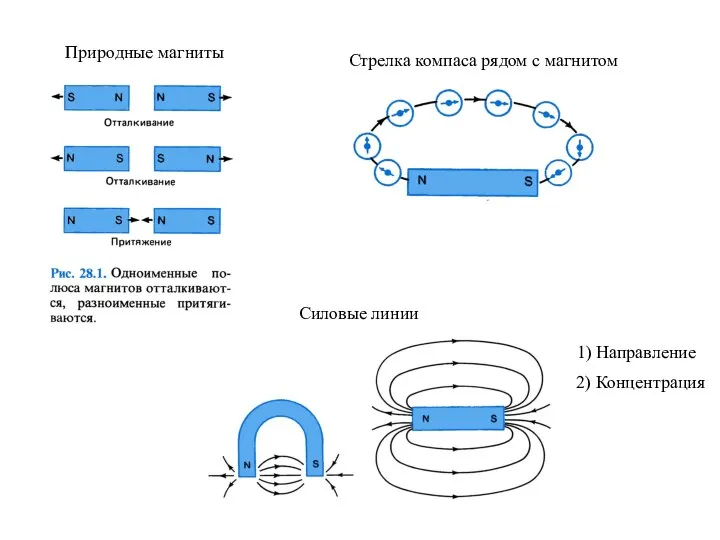 Природные магниты
Природные магниты L2_1_Mekhanicheskie_kharakteristiki_metallov
L2_1_Mekhanicheskie_kharakteristiki_metallov Реостаты
Реостаты Оптимизация методики разделения лечебного препарата Clopidogrel Hydrogen Sulfate с сопутствующей примесью (А)
Оптимизация методики разделения лечебного препарата Clopidogrel Hydrogen Sulfate с сопутствующей примесью (А) Интерактивная игра по физике Эрудит. Для учащихся 7 класса
Интерактивная игра по физике Эрудит. Для учащихся 7 класса Изменения агрегатных состояний вещества. Физический диктант
Изменения агрегатных состояний вещества. Физический диктант Решение задач на расчёт КПД теплового двигателя. 8 класс
Решение задач на расчёт КПД теплового двигателя. 8 класс Методы обзора пространства и измерения координат
Методы обзора пространства и измерения координат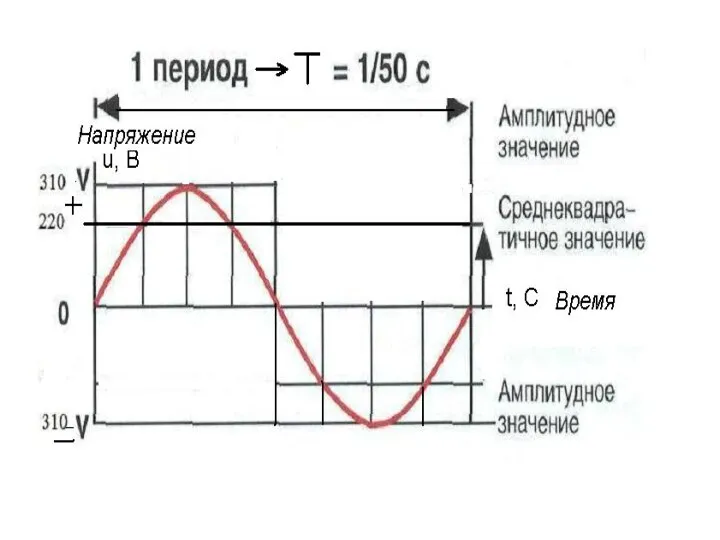 Действующее и среднее значение синусоидального тока
Действующее и среднее значение синусоидального тока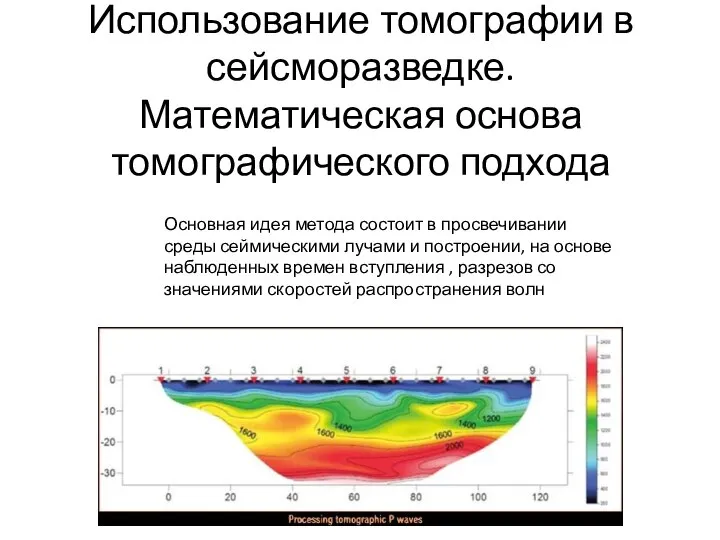 Использование томографии в сейсморазведке. Математическая основа томографического подхода
Использование томографии в сейсморазведке. Математическая основа томографического подхода Закон Ома для участка цепи
Закон Ома для участка цепи Давление газа
Давление газа Основные положения технической термодинамики
Основные положения технической термодинамики Ток, протекающий в нейтралях трансформаторов и автотрансформаторов при КЗ на землю
Ток, протекающий в нейтралях трансформаторов и автотрансформаторов при КЗ на землю Физика на рыбалке
Физика на рыбалке Инерция в жизни человека
Инерция в жизни человека Движение жидкостей и газов. Закон Бернулли
Движение жидкостей и газов. Закон Бернулли Динамика. Законы механики Ньютона
Динамика. Законы механики Ньютона Переменный ток
Переменный ток В мире звуков
В мире звуков Реактивное движение
Реактивное движение