Фильтры с бесконечной импульсной характеристикой. Синтез БИХ-фильтров методом билинейного Z-преобразования''
Содержание
- 2. Учебные цели: Кафедра №2, ВАС Изучить содержание билинейного Z-преобразования. Изучить методику синтеза цифровых БИХ-фильтров при билинейном
- 3. Учебные вопросы: Кафедра №2, ВАС Определение билинейного Z-преобразования. Свойства билинейного Z-преобразования. Методика синтеза БИХ-фильтров.
- 4. Литература для самостоятельной работы обучаемых: Кафедра №2, ВАС 1. Основы цифровой обработки сигналов: Курс лекций./ Авторы:
- 5. Первый учебный вопрос Кафедра №2, ВАС Определение билинейного Z-преобразования
- 6. Первый учебный вопрос Кафедра №2, ВАС
- 7. Первый учебный вопрос Кафедра №2, ВАС
- 8. Первый учебный вопрос Кафедра №2, ВАС
- 9. Второй учебный вопрос Кафедра №2, ВАС Свойства билинейного Z-преобразования
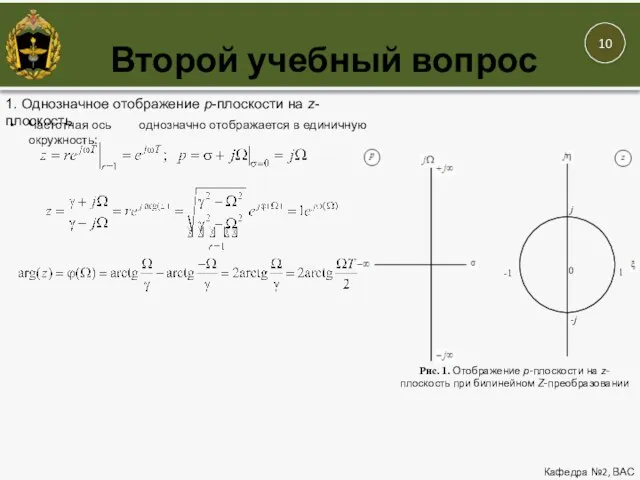
- 10. Второй учебный вопрос Кафедра №2, ВАС 1. Однозначное отображение p-плоскости на z-плоскость Частотная ось однозначно отображается
- 11. Второй учебный вопрос Кафедра №2, ВАС 1. Однозначное отображение p-плоскости на z-плоскость Частотная ось однозначно отображается
- 12. Второй учебный вопрос Кафедра №2, ВАС 1. Однозначное отображение p-плоскости на z-плоскость Частотная ось однозначно отображается
- 13. Второй учебный вопрос Кафедра №2, ВАС 1. Однозначное отображение p-плоскости на z-плоскость Частотная ось однозначно отображается
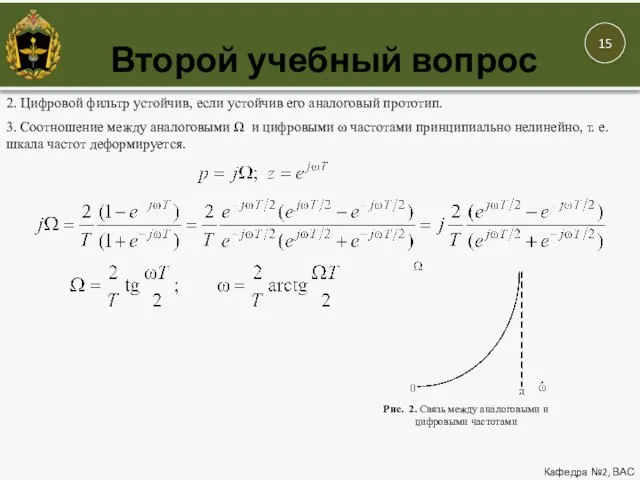
- 14. Второй учебный вопрос Кафедра №2, ВАС 2. Цифровой фильтр устойчив, если устойчив его аналоговый прототип. 3.
- 15. Второй учебный вопрос Кафедра №2, ВАС 2. Цифровой фильтр устойчив, если устойчив его аналоговый прототип. 3.
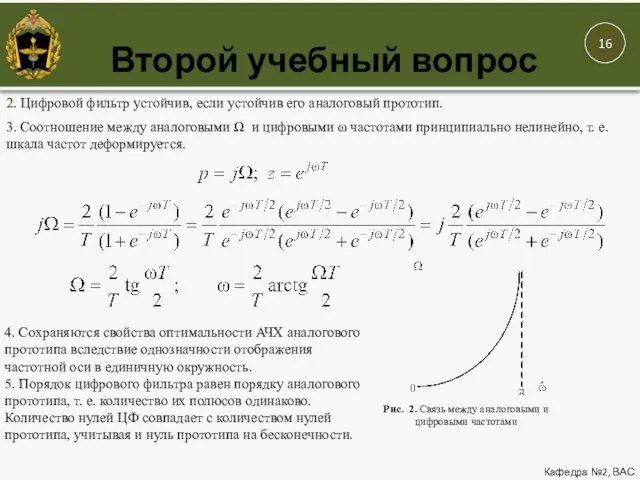
- 16. Второй учебный вопрос Кафедра №2, ВАС 2. Цифровой фильтр устойчив, если устойчив его аналоговый прототип. 3.
- 17. Второй учебный вопрос Кафедра №2, ВАС Пример 1
- 18. Второй учебный вопрос Кафедра №2, ВАС Пример 1 6. Деформация шкалы частот означает, что метод билинейного
- 19. Третий учебный вопрос Кафедра №2, ВАС Методика синтеза цифрового фильтра при билинейном Z-преобразовании
- 20. Третий учебный вопрос Кафедра №2, ВАС Рис. 3. Задание требований к цифровому фильтру и аналоговому прототипу:
- 21. Третий учебный вопрос Кафедра №2, ВАС Рис. 3. Задание требований к цифровому фильтру и аналоговому прототипу:
- 22. Третий учебный вопрос Кафедра №2, ВАС
- 23. Третий учебный вопрос Кафедра №2, ВАС Рис. 4. Принцип объединения нулей и полюсов в биквадратные звенья
- 24. Третий учебный вопрос Кафедра №2, ВАС Рис. 4. Принцип объединения нулей и полюсов в биквадратные звенья
- 25. Третий учебный вопрос Кафедра №2, ВАС Рис. 4. Принцип объединения нулей и полюсов в биквадратные звенья
- 26. Заключение Кафедра №2, ВАС Изученный метод синтеза БИХ-фильтров используется очень широко, в том числе и для
- 28. Скачать презентацию






















 Электрический ток
Электрический ток Маятниковые копры
Маятниковые копры Link Stabilizer maintenance judjement standart
Link Stabilizer maintenance judjement standart Закон сохранения импульса
Закон сохранения импульса Сложение сил
Сложение сил Роль русских ученых в развитии электротехники
Роль русских ученых в развитии электротехники Расчет износа деталей транспортных средств
Расчет износа деталей транспортных средств Исследование схемы измерения сопротивления заземлителя МС-08
Исследование схемы измерения сопротивления заземлителя МС-08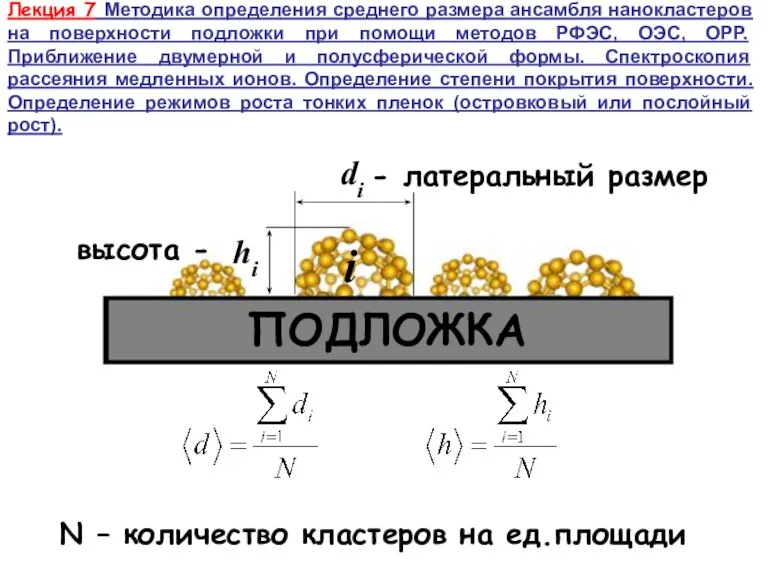 Методика определения среднего размера ансамбля нанокластеров на поверхности подложки при помощи методов РФЭС, ОЭС, ОРР
Методика определения среднего размера ансамбля нанокластеров на поверхности подложки при помощи методов РФЭС, ОЭС, ОРР Презентация на тему Оптические приборы (11 класс)
Презентация на тему Оптические приборы (11 класс)  Назначение и устройство шатунов, шатунных подшипников и поршней дизелей. Порядок расположения кривошипов валов
Назначение и устройство шатунов, шатунных подшипников и поршней дизелей. Порядок расположения кривошипов валов Транспортные, транспортирующие и погрузочно-разгрузочные машины. Тема 2
Транспортные, транспортирующие и погрузочно-разгрузочные машины. Тема 2 3_ЭМКолебания
3_ЭМКолебания Электрический заряд, электризация
Электрический заряд, электризация Кең ауқымды вибратор
Кең ауқымды вибратор Сопротивление материалов. Построение эпюр внутренних силовых факторов в кривом брусе
Сопротивление материалов. Построение эпюр внутренних силовых факторов в кривом брусе Законы Ньютона (10 класс)
Законы Ньютона (10 класс) Презентация на тему Постоянные магниты. Магнитное поле Земли
Презентация на тему Постоянные магниты. Магнитное поле Земли 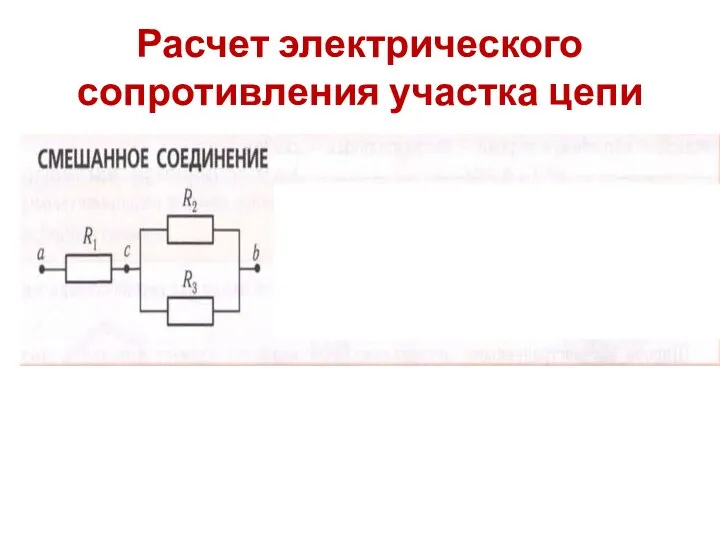 Расчёт сопротивления электрических цепей
Расчёт сопротивления электрических цепей Магнитное поле
Магнитное поле Нагревание проводников электрическим током. Закон Джоуля-Ленца
Нагревание проводников электрическим током. Закон Джоуля-Ленца Сила упругости
Сила упругости Релятивистская динамика
Релятивистская динамика Формообразование на станках
Формообразование на станках Презентация на тему Зрение
Презентация на тему Зрение  Внутренняя энергия
Внутренняя энергия Презентация на тему Викторина по физике
Презентация на тему Викторина по физике  Презентация на тему Явление электромагнитной индукции
Презентация на тему Явление электромагнитной индукции