Электротехника и электроника. Анализ и расчет переходных процессов в электрических цепях

АНАЛИЗ И РАСЧЕТ ПЕРЕХОДНЫХ ПРОЦЕССОВ В
ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
Тема 4

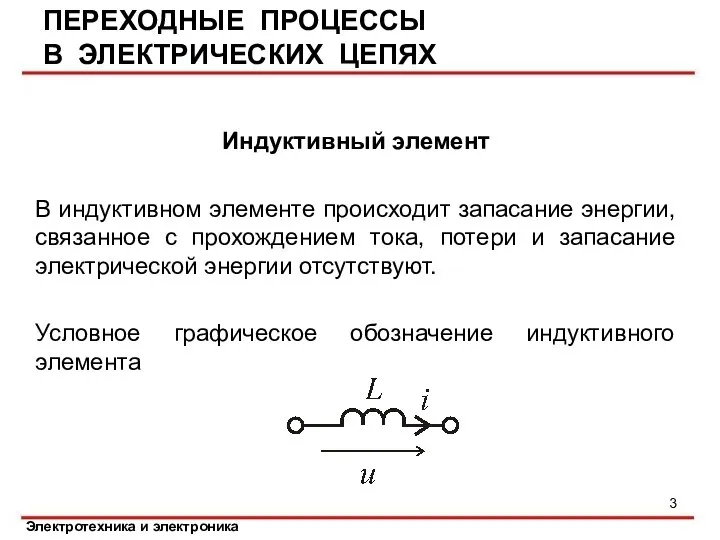
ПЕРЕХОДНЫЕ ПРОЦЕССЫ
В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
Индуктивный элемент
В индуктивном элементе происходит запасание энергии, связанное с прохождением тока, потери и запасание электрической энергии отсутствуют.
Условное графическое обозначение индуктивного элемента

Электротехника и электроника
Индуктивные элементы

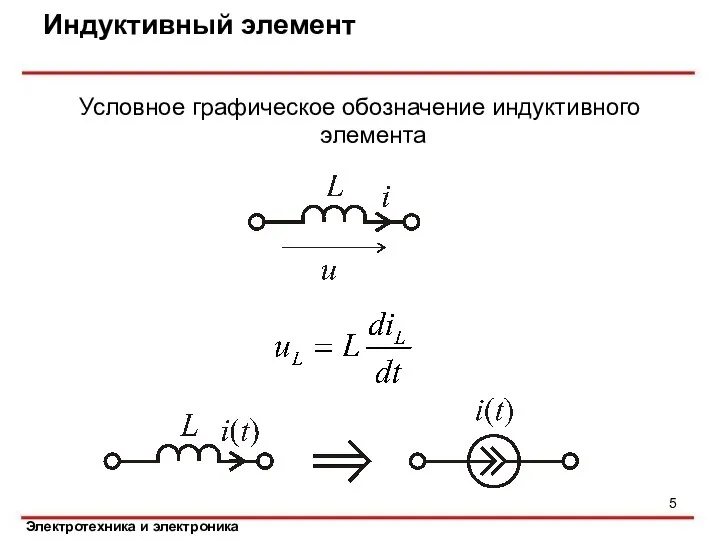
Индуктивный элемент
Условное графическое обозначение индуктивного элемента

Емкостный элемент
Емкостный элемент
В идеальном емкостном элементе происходит запасание электрической энергии, связанное с прохождением тока, потери и запасание магнитной энергии отсутствуют.

Электротехника и электроника
Конденсаторы

Законы коммутации и начальные условия
Законы коммутации
В начальный момент после коммутации токи индуктивных и напряжения емкостных элементов остаются такими же, какими они были перед коммутацией, а затем плавно изменяются.

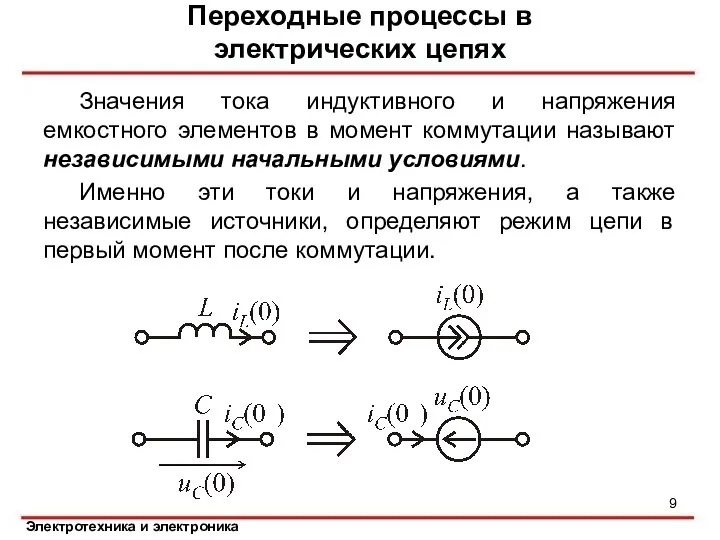
Значения тока индуктивного и напряжения емкостного элементов в момент коммутации называют независимыми начальными условиями.
Именно эти токи и напряжения, а также независимые источники, определяют режим цепи в первый момент после коммутации.
Переходные процессы в
электрических цепях

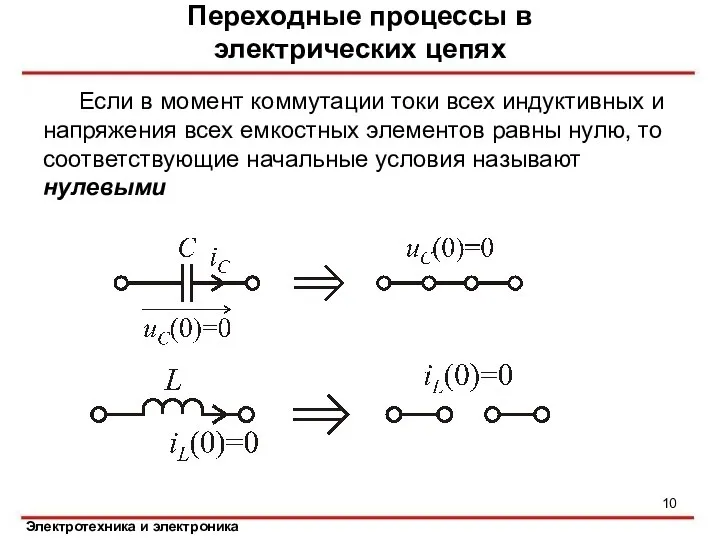
Если в момент коммутации токи всех индуктивных и напряжения всех емкостных элементов равны нулю, то соответствующие начальные условия называют нулевыми
Переходные процессы в
электрических цепях

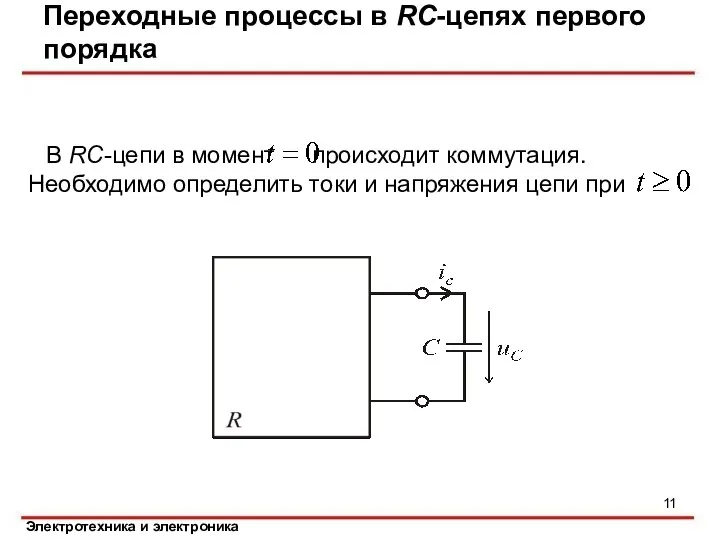
Переходные процессы в RC-цепях первого порядка

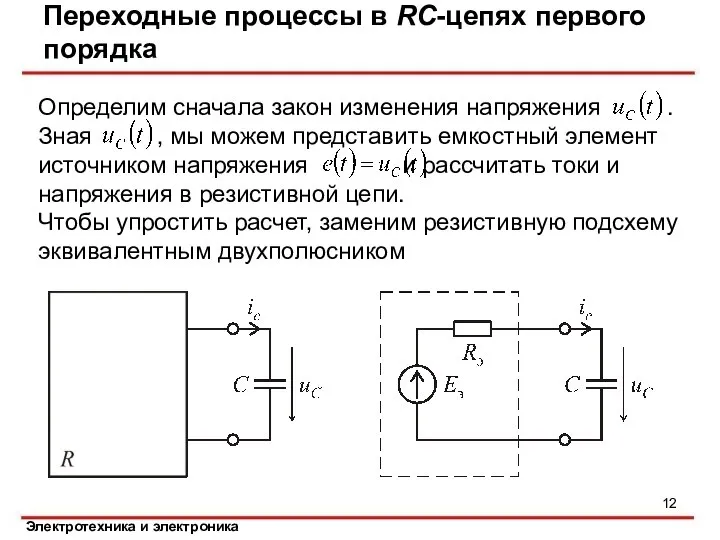
Переходные процессы в RC-цепях первого порядка
Определим сначала закон изменения напряжения .
Зная , мы можем представить емкостный элемент источником напряжения и рассчитать токи и напряжения в резистивной цепи.
Чтобы упростить расчет, заменим резистивную подсхему эквивалентным двухполюсником

Выполняя подстановку и решая
полученное уравнение относительно , получим
Переходные процессы в RC-цепях первого порядка
- постоянная времени.
(1)
(2)
В соответствии со вторым законом Кирхгофа:

Первое слагаемое в (3) - свободная составляющая
Второе слагаемое в (3) - принужденная (установившаяся) составляющая
Переходные процессы в RC-цепях первого порядка
(3)

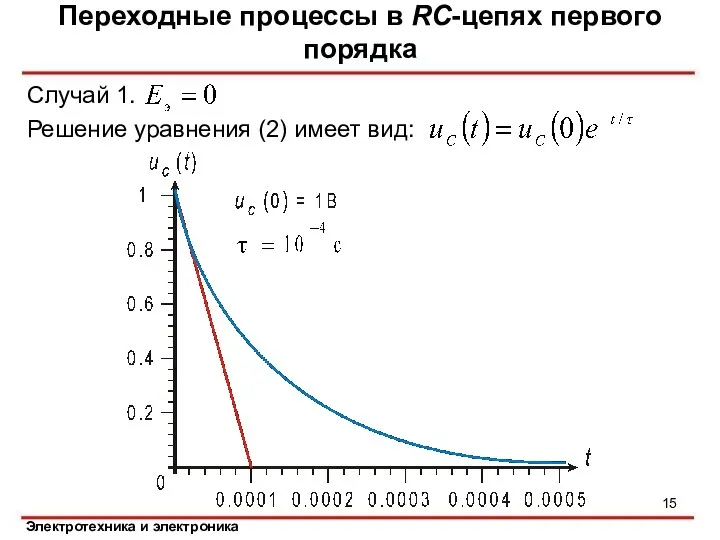
Случай 1.
Решение уравнения (2) имеет вид:
Переходные процессы в RC-цепях первого порядка

Случай 2.
Переходные процессы в RC-цепях первого порядка
Решение:
Поскольку
Запишем уравнение (2) в виде:

Порядок расчета переходных процессов в RC-цепях первого порядка
Считаем, что переходный процесс вызван замыканием или размыканием идеального ключа в момент t = 0 и нужно определить ток k-й ветви.
1. Анализируем цепь в момент, предшествующий коммутации (при t = 0-), и определяем напряжение емкостного элемента UC (0).
2. Заменяем емкостный элемент источником напряжения E = UC (0) (рис. а). Анализируя полученную резистивную схему замещения, находим начальные
значения искомых токов и напряжений

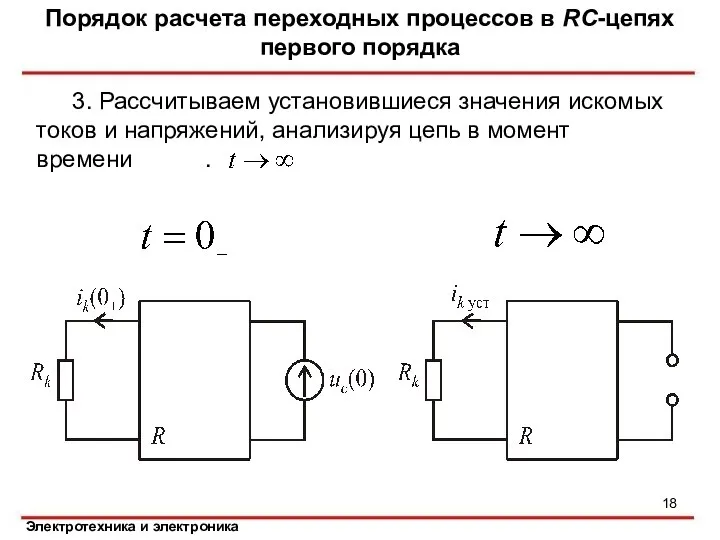
3. Рассчитываем установившиеся значения искомых токов и напряжений, анализируя цепь в момент времени .
Порядок расчета переходных процессов в RC-цепях первого порядка

4. Определяем входное сопротивление резистивной цепи со стороны зажимов, к которым подключен емкостный элемент. Рассчитываем постоянную времени цепи по формуле
5. Решение записываем в виде
Важно! Все переходные токи и напряжения имеют одинаковую постоянную времени.
Порядок расчета переходных процессов в RC-цепях первого порядка.

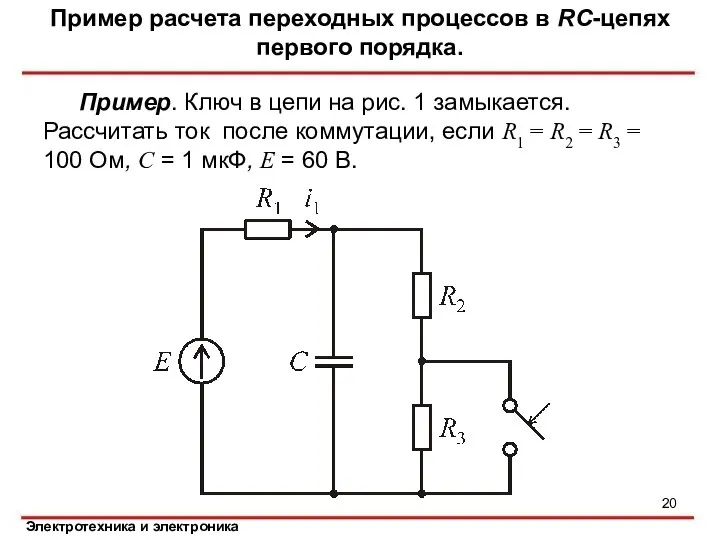
Пример. Ключ в цепи на рис. 1 замыкается. Рассчитать ток после коммутации, если R1 = R2 = R3 = 100 Ом, C = 1 мкФ, E = 60 В.
Пример расчета переходных процессов в RC-цепях первого порядка.

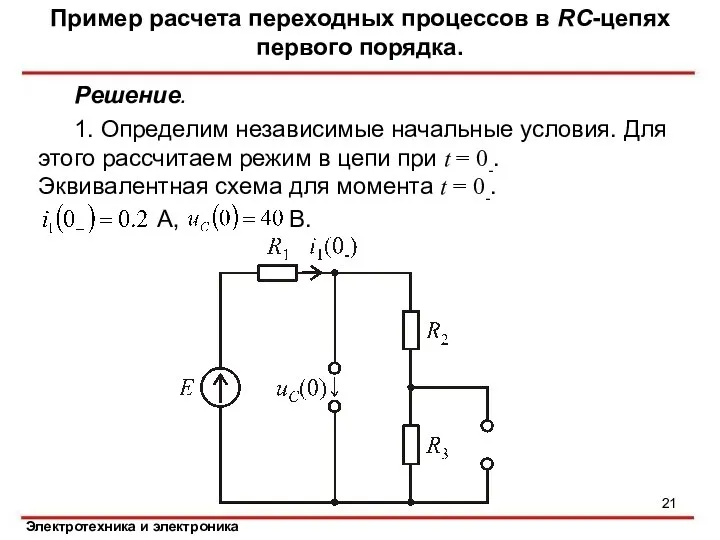
Решение.
1. Определим независимые начальные условия. Для этого рассчитаем режим в цепи при t = 0-. Эквивалентная схема для момента t = 0-.
А,
В.
Пример расчета переходных процессов в RC-цепях первого порядка.

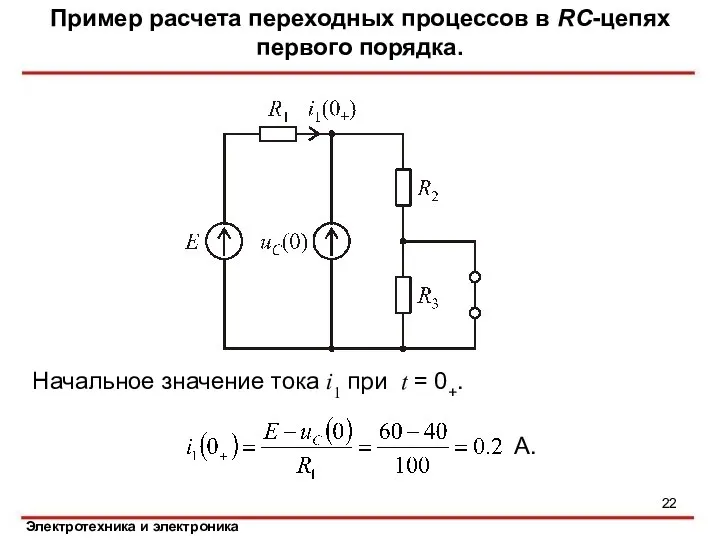
Начальное значение тока i1 при t = 0+.
Пример расчета переходных процессов в RC-цепях первого порядка.
А.

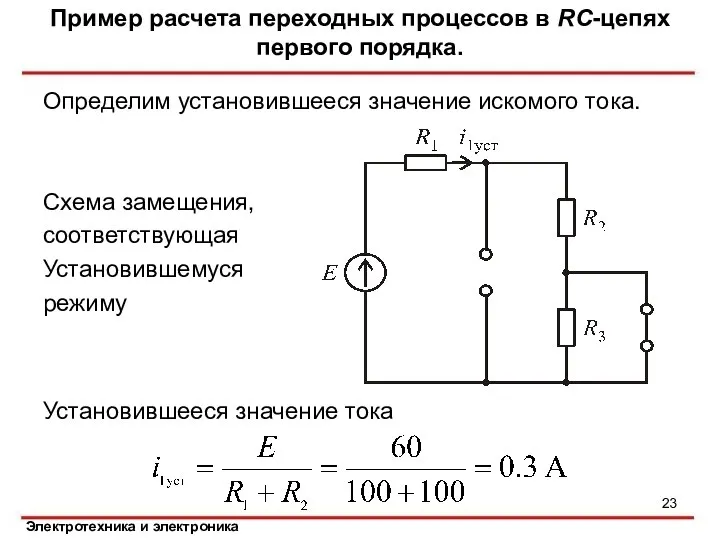
Определим установившееся значение искомого тока.
Схема замещения,
соответствующая
Установившемуся
режиму
Установившееся значение тока
Пример расчета переходных процессов в RC-цепях первого порядка.

Определим входное сопротивление схемы относительно зажимов, к которым подключен емкостный элемент. Исключая источник напряжения, найдем, что
Пример расчета переходных процессов в RC-цепях первого порядка.
Постоянная времени цепи
Закон изменения тока

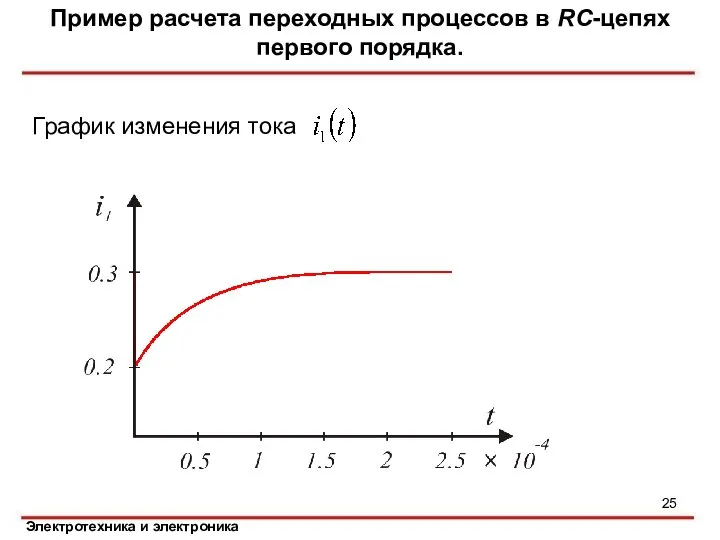
Пример расчета переходных процессов в RC-цепях первого порядка.
График изменения тока

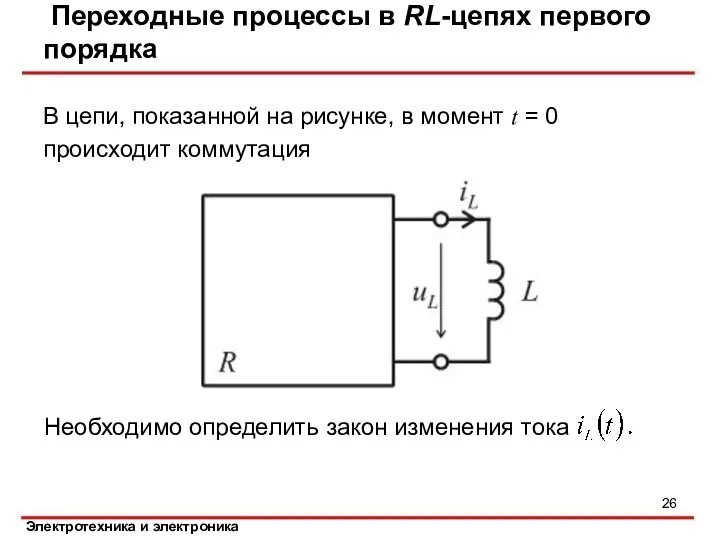
Переходные процессы в RL-цепях первого порядка
В цепи, показанной на рисунке, в момент t = 0
происходит коммутация
Необходимо определить закон изменения тока

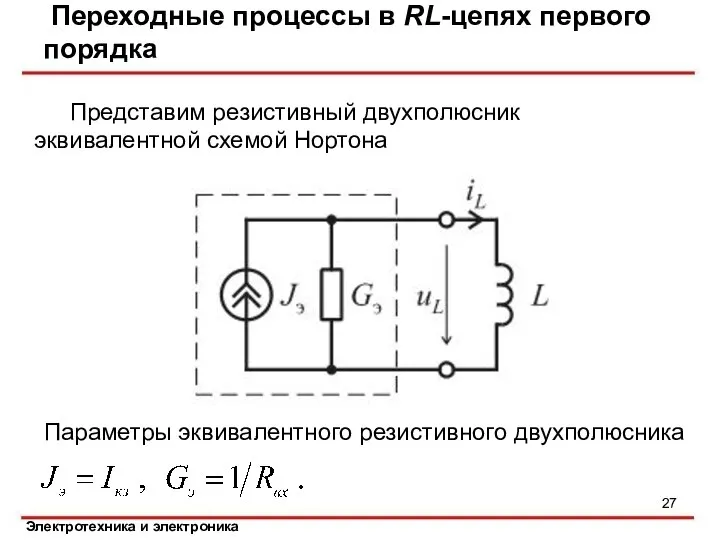
Представим резистивный двухполюсник эквивалентной схемой Нортона
Переходные процессы в RL-цепях первого порядка
Параметры эквивалентного резистивного двухполюсника

Переходные процессы в RL-цепях первого порядка
Уравнение по первому закону Кирхгофа:
Учитывая, что , запишем уравнение состояния:
(1)

Решение уравнения (2) можно представить в следующем виде:
Переходные процессы в RL-цепях первого порядка
(2)
называют постоянной времени.

Порядок расчета переходных процессов в RL-цепях первого порядка.
Переходный процесс вызван замыканием или размыканием идеального ключа в момент t = 0.
1. Анализируем цепь в момент, предшествующий коммутации (при t = 0-), и определяем ток индуктивного элемента iL(0).
2. Заменяем индуктивный элемент источником тока iL(0). Анализируя полученную схему замещения, определим начальные значения искомых напряжений или токов .
Переходные процессы в RL-цепях первого порядка

Переходные процессы в RL-цепях первого порядка
3. Замыкаем накоротко зажимы, к которым подключен индуктивный элемент. Определяем установившиеся значения интересующих нас токов и напряжений .
4. Определяем входное сопротивление резистивной цепи со стороны зажимов, к которым подключен индуктивный элемент. Рассчитываем постоянную времени цепи по формуле или .
5. Записываем решение в виде

Электротехника и электроника
Рекомендуемая литература
1. Алтунин Б.Ю., Панкова Н.Г. Теоретические основы электротехники:
Комплекс учебно - методических материалов: Часть 1 / Б.Ю. Алтунин,
Н.Г. Панкова; НГТУ им. Р.Е. Алексеева. Н.Новгород, 2007.-130 с.
2. Алтунин Б.Ю., Кралин А.А. Электротехника и электроника: комплекс учебно-методических материалов: Ч.1/ Б.Ю. Алтунин, А.А. Кралин; НГТУ
им. Р.Е. Алексеева. Н.Новгород, 2007.-98 с.
3. Алтунин Б.Ю., Кралин А.А. Электротехника и электроника: комплекс учебно-методических материалов: Ч.2/ Б.Ю. Алтунин, А.А. Кралин; НГТУ
им. Р.Е. Алексеева. Н.Новгород, 2008.-98 с
4. Касаткин, А.С. Электротехника /А.С. Касаткин, М.В. Немцов.-М.: Энергоатомиздат, 2000.
5. Справочное пособие по основам электротехники и электроники /под. ред. А.В. Нетушила.-М.: Энергоатомиздат, 1995.
6. Манаев Е.И. Основы радиоэлектроники.-3-е изд., перераб. И доп.-М.: Радио и связь, 1990.-512 с.: ил.
7. Новожилов, О. П. Электротехника и электроника: учебник / О. П. Новожилов. – М.: Гардарики, 2008. – 653 с.