Содержание
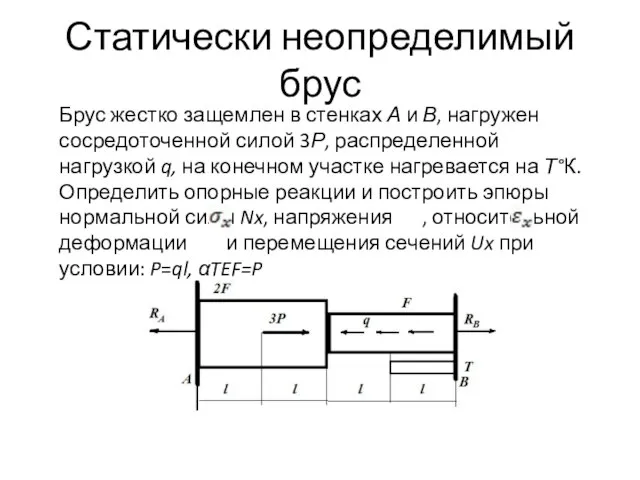
- 2. Статически неопределимый брус Брус жестко защемлен в стенках А и В, нагружен сосредоточенной силой 3Р, распределенной
- 3. Составление расчетной схемы и запись уравнения равновесия Для бруса при растяжении или сжатии можно записать только
- 4. Раскрытие статической неопределимости Для раскрытия статической неопределимости осуществляется переход к статически определимому стержню, эквивалентному заданному, путем
- 5. Есть два подхода к записи уравнения перемещений UB=0. Первый рассматривает перемещение UB как сумму накопленных деформаций
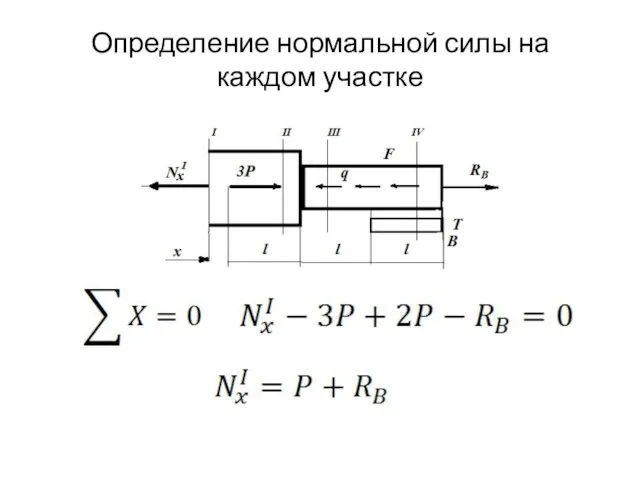
- 6. Определение нормальной силы на каждом участке
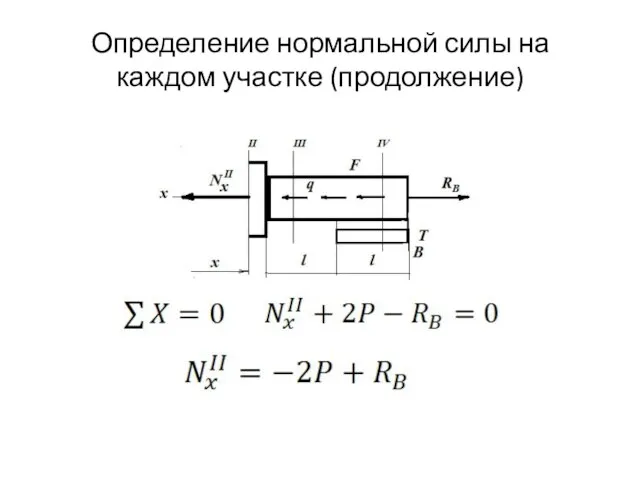
- 7. Определение нормальной силы на каждом участке (продолжение)
- 8. Определение нормальной силы на каждом участке (продолжение)
- 9. Определение деформации каждого участка и запись уравнения перемещения сечения В откуда
- 10. Второй подход к записи уравнения перемещений UB=0. Используется принцип независимости действия сил где
- 11. Определение нормальной силы, напряжения, относительной деформации и перемещения в сечениях бруса (стержня) Нормальную силу в каждом
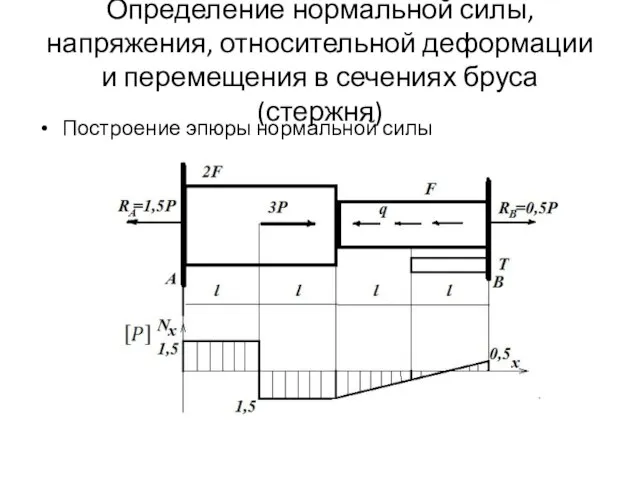
- 12. Определение нормальной силы, напряжения, относительной деформации и перемещения в сечениях бруса (стержня) Построение эпюры нормальной силы
- 13. Определение напряжения, относительной деформации и перемещения в сечениях бруса (стержня) Определение напряжений Определение деформаций
- 14. Определение нормальной силы, напряжения, относительной деформации и перемещения в сечениях бруса (стержня) Определение перемещений сечений
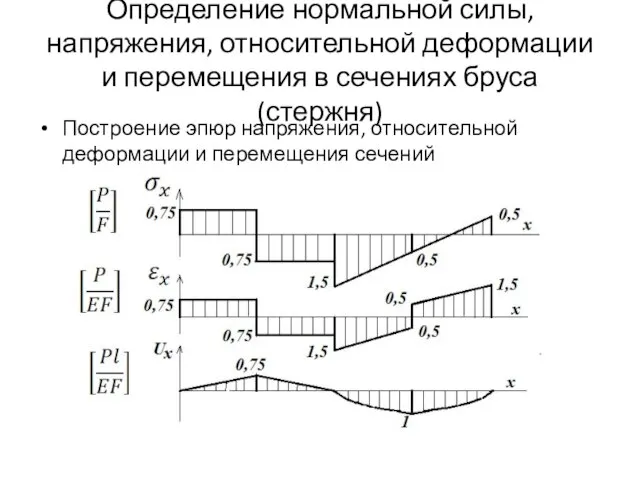
- 15. Определение нормальной силы, напряжения, относительной деформации и перемещения в сечениях бруса (стержня) Построение эпюр напряжения, относительной
- 16. Температурная деформация статически неопределимого бруса Брус, состоящий из двух участков, жестко защемлен между двумя стенками. Второй
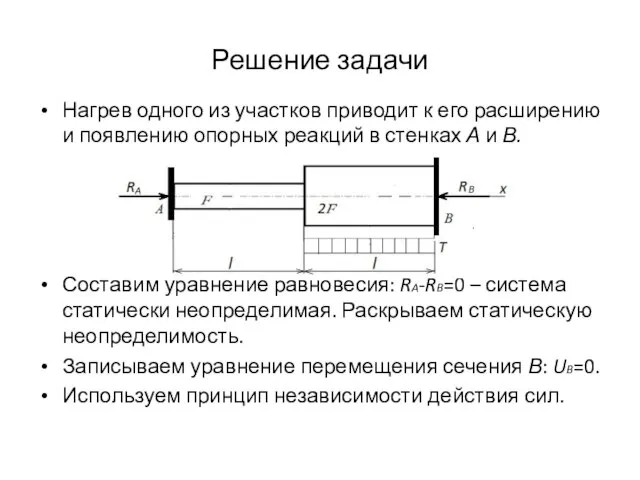
- 17. Решение задачи Нагрев одного из участков приводит к его расширению и появлению опорных реакций в стенках
- 18. Решение задачи
- 20. Скачать презентацию











 Литье металлов. Электромагнитная волна
Литье металлов. Электромагнитная волна ЭДС индукции в движущихся проводниках
ЭДС индукции в движущихся проводниках Автомобильные газоанализаторы
Автомобильные газоанализаторы Рабочие вещества холодильных машин и тепловых насосов
Рабочие вещества холодильных машин и тепловых насосов Методы исследования частиц
Методы исследования частиц Теплообмен и уравнение теплового баланса
Теплообмен и уравнение теплового баланса Теория цвета Ньютона
Теория цвета Ньютона Дифракция света
Дифракция света Состав атомного ядра. . Объяснение электрических явлений
Состав атомного ядра. . Объяснение электрических явлений Кинематика
Кинематика Контакты, контактные материалы, припои и флюсы
Контакты, контактные материалы, припои и флюсы Дисковый тормоз
Дисковый тормоз История изобретения и развития тепловых двигателей
История изобретения и развития тепловых двигателей Магнитное взаимодействие Изучение свойств магнита Учитель И.А. Попова
Магнитное взаимодействие Изучение свойств магнита Учитель И.А. Попова Методы наблюдения и регистрации элементарных частиц
Методы наблюдения и регистрации элементарных частиц Презентация на тему Физическая игра "Ваше слово, эрудиты"
Презентация на тему Физическая игра "Ваше слово, эрудиты"  Устройство геодезического прибора теодолита
Устройство геодезического прибора теодолита Передача давления жидкостями и газами. Закон Паскаля
Передача давления жидкостями и газами. Закон Паскаля Решение задач по теме Электромагнитная индукция
Решение задач по теме Электромагнитная индукция "Масса тела. Плотность вещества".
"Масса тела. Плотность вещества". Прямолинейное равноускоренное движение. Решение задач
Прямолинейное равноускоренное движение. Решение задач Решение задач на вычисление массы продукта реакции по известной массе исходного вещества, содержащего примеси
Решение задач на вычисление массы продукта реакции по известной массе исходного вещества, содержащего примеси сила Архимеда сила выталкивающая тело из жидкости
сила Архимеда сила выталкивающая тело из жидкости Конкурс Физические опыты
Конкурс Физические опыты Методы и приёмы решения задач по физике
Методы и приёмы решения задач по физике Виды заклёпочных соединений и способы их выполнения
Виды заклёпочных соединений и способы их выполнения Теория горения и взрывов. Переход горения в детонацию. Взрыв. Лекция 10
Теория горения и взрывов. Переход горения в детонацию. Взрыв. Лекция 10 Постоянный ток. Электрический ток в различных средах
Постоянный ток. Электрический ток в различных средах