Слайд 2Волновая функция.
Уравнение Шрёдингера.
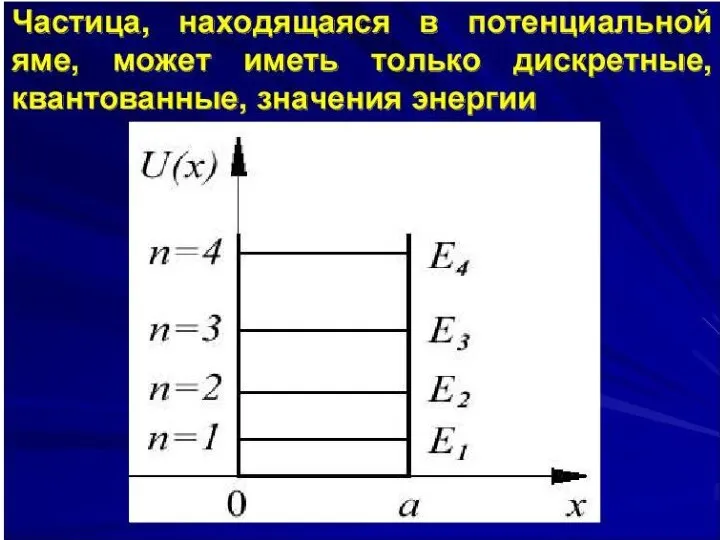
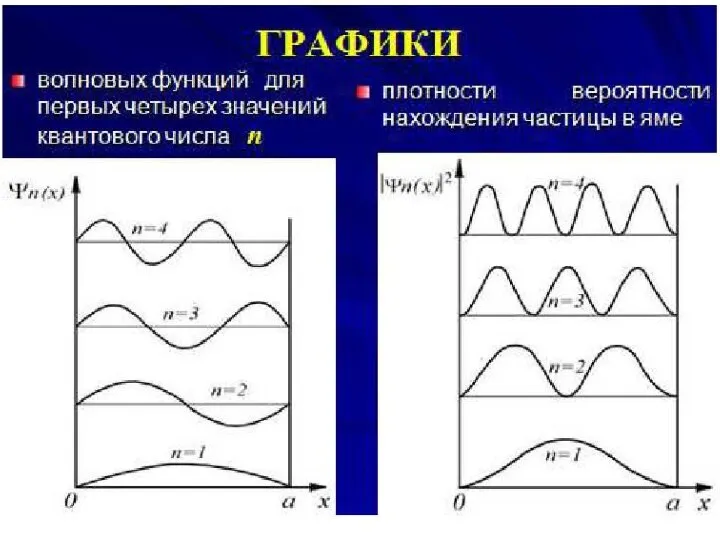
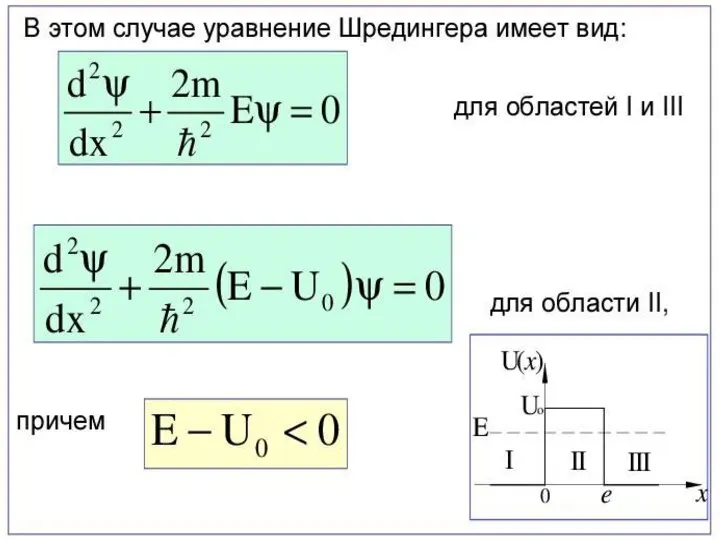
Частица в одномерной потенциальной яме бесконечной глубины.
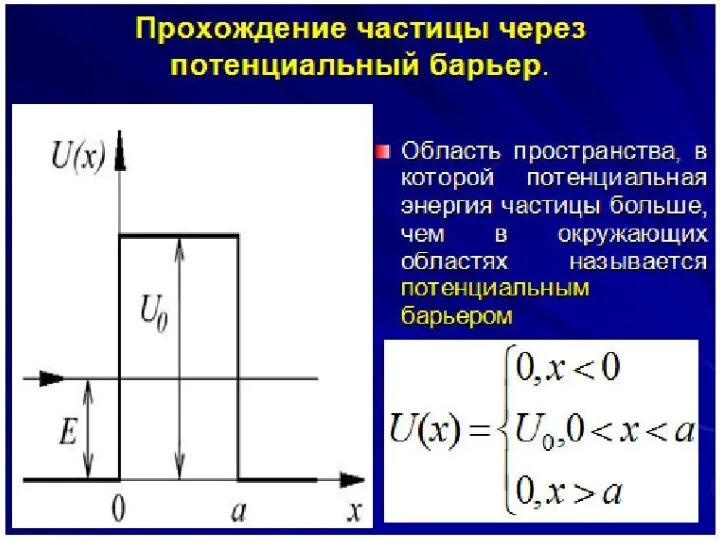
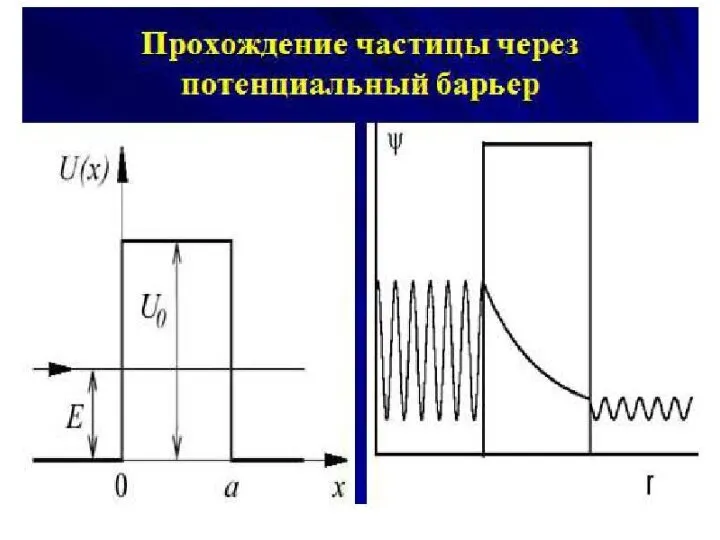
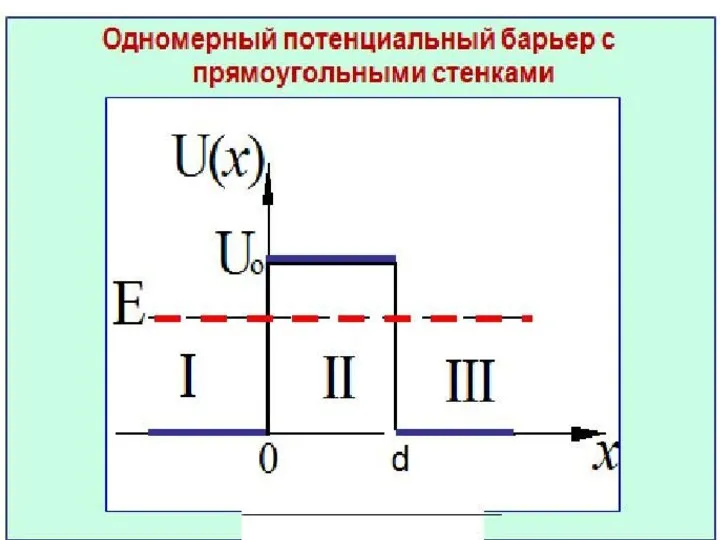
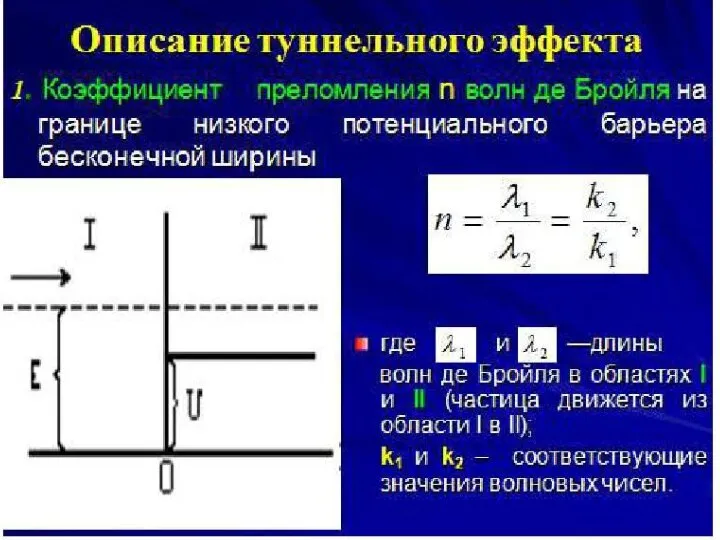
Туннельный эффект.
План лекции

Слайд 3Основные понятия
Масса микрочастицы - m: определяет её корпускулярные свойства.
2. Потенциальная энергия U(х,

у, z, t): определяет взаимодействие частицы с силовым полем.
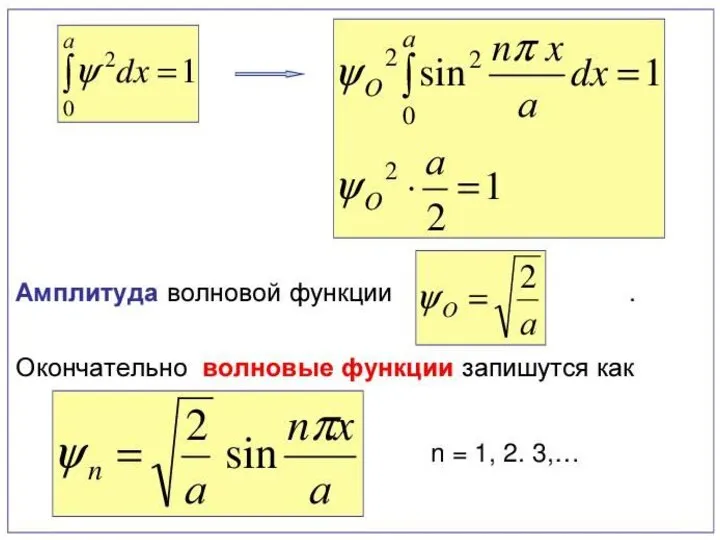
3. «Пси»-функция (х, у, z, t): определяет волновые свойства микрочастицы.
является также функцией координат и времени.
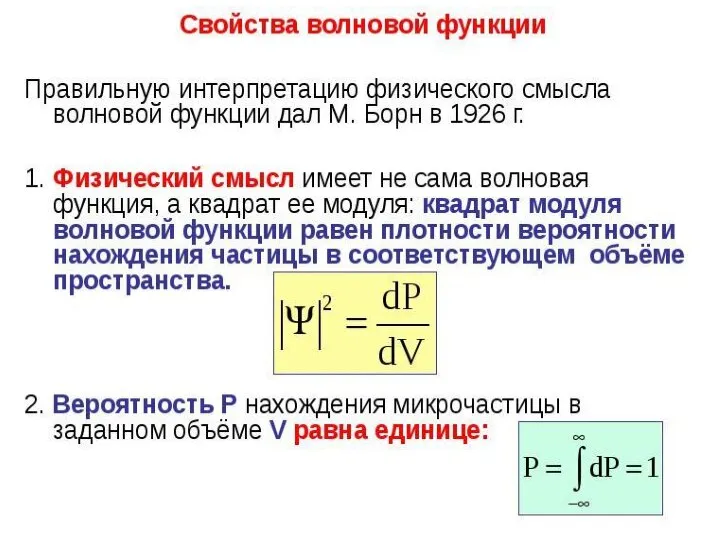
Слайд 4Волновая функция
Состояние микрочастицы в квантовой механике описывается заданием волновой функции, являющейся функцией

пространственных координат и времени.
Слайд 10Эрвин ШРЁДИНГЕР (Schrodinger)
Австрийский физик
родился в Вене
(1887 г. - 1961

г.)
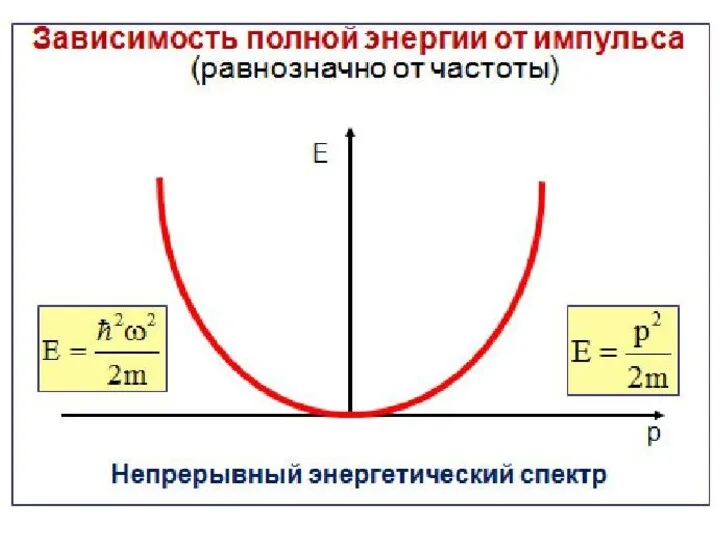
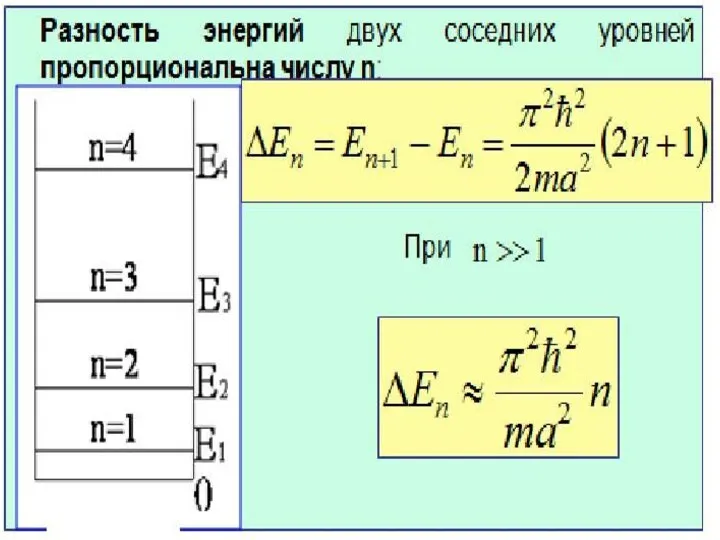
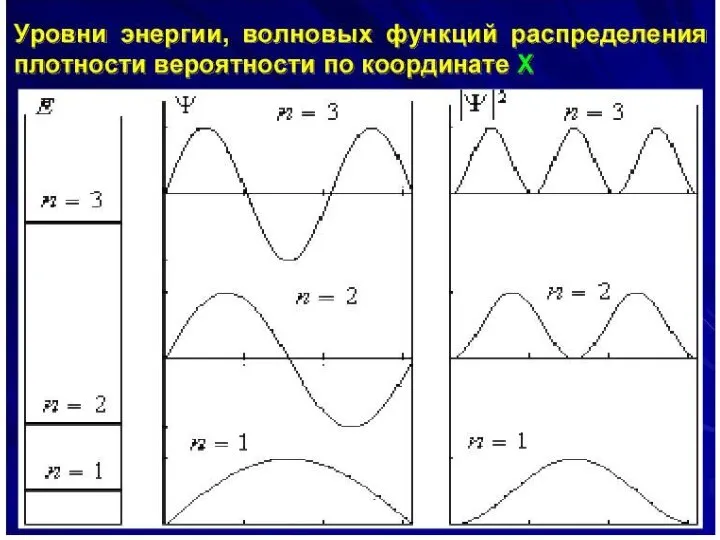
Слайд 31Особенности энергетического спектра
1. Полная энергия частицы положительная ( ).
2. Полная энергия квантуется:

принимает дискретный набор значений, причём
Энергия первого (основного) состояния:
3. Энергетический спектр является расходящимся, поскольку расстояния между уровнями увеличиваются.
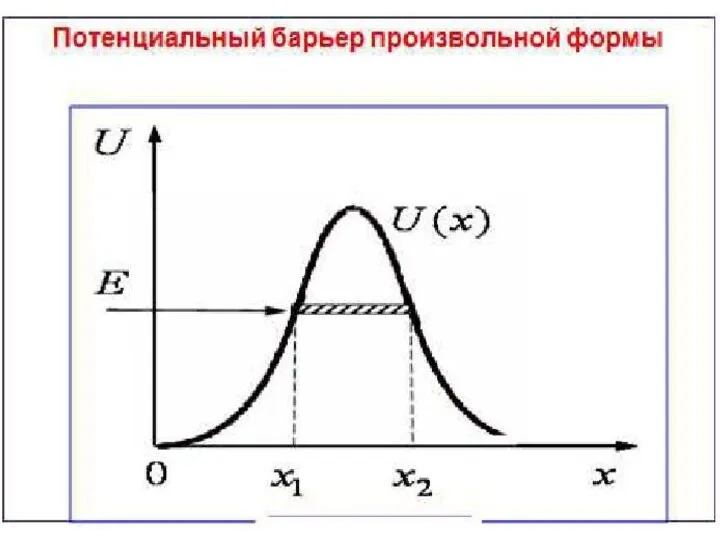
Слайд 53Решение данной задачи является сложным, поэтому ограничимся основными выводами.
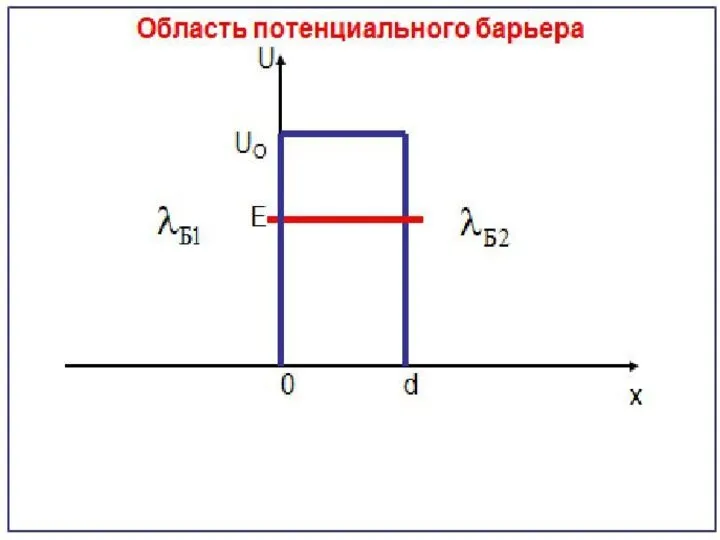
Что происходит с микрочастицей

в области потенциального барьера - неизвестно.
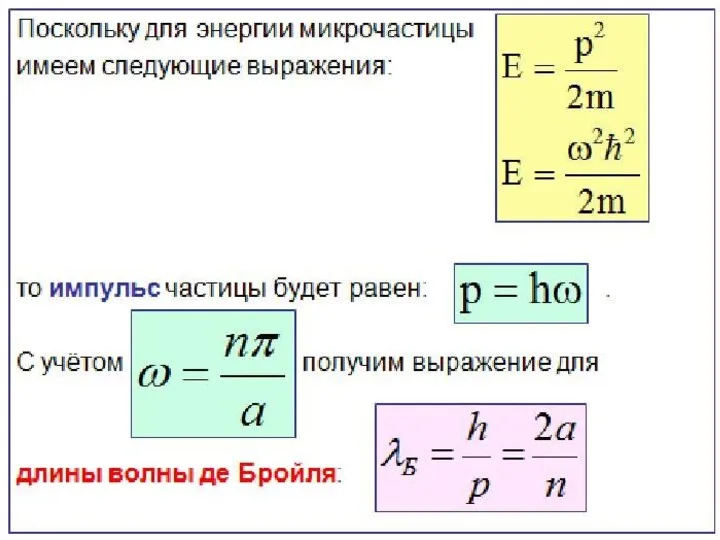
Достоверно известно лишь то, что частица была перед барьером, имея длину волны де Бройля , и стала находиться в области за потенциальным барьером, изменив свои волновые свойства и обладая длиной волны де Бройля .
Слайд 56 Поскольку в области потенциального барьера для квантовой частицы «работает» соотношение неопределённостей,

то координата и импульс частицы не могут иметь определенных значений.
Это означает, что не могут быть одновременно точно определены кинетическая ЕК и потенциальная U энергии.
Кинетическая энергия зависит от импульса, а потенциальная от координат.
Слайд 57Таким образом, хотя полная энергия частицы имеет определенное значение Е, она не

может быть представлена в виде суммы точно определенных энергий ЕК и U.
Ясно, что в этом случае заключение об отрицательности кинетической энергии ЕК «внутри туннеля» становится бессмысленным.



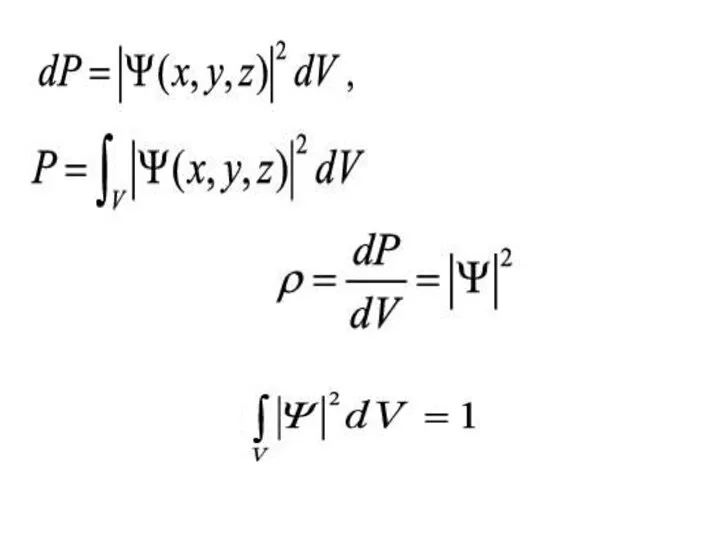















































 Кодирование и обработка звуковой информации
Кодирование и обработка звуковой информации Введение в теорию электромагнитного поля. Лекция №7
Введение в теорию электромагнитного поля. Лекция №7 Задачи на движение. Движение протяженных тел
Задачи на движение. Движение протяженных тел Резание слесарной ножовкой. 6класс
Резание слесарной ножовкой. 6класс Частицы с отрицательной энергией в эргосфере чёрных дыр
Частицы с отрицательной энергией в эргосфере чёрных дыр Механические колебания и волны. Решение задач
Механические колебания и волны. Решение задач ЭДС индукции в движущихся проводниках
ЭДС индукции в движущихся проводниках Механічна робота. Потужність
Механічна робота. Потужність Электромагнитная индукция
Электромагнитная индукция Распространение колебаний в упругих средах. Волны. 9 класс
Распространение колебаний в упругих средах. Волны. 9 класс Исследование радиотехнической системы контроля положения нарушителя
Исследование радиотехнической системы контроля положения нарушителя Техническое обслуживание, диагностирование и ремонт жидкостной системы охлаждения автомобильного двигателя
Техническое обслуживание, диагностирование и ремонт жидкостной системы охлаждения автомобильного двигателя Подход Лагранжа
Подход Лагранжа Электролиз. Постоянный ток
Электролиз. Постоянный ток Распределение Бозе-Эйнштейна. Конденсация Бозе-газа. Температура конденсации. Число частиц в конденсате
Распределение Бозе-Эйнштейна. Конденсация Бозе-газа. Температура конденсации. Число частиц в конденсате Презентация на тему Поле чудес Галилео Галилей
Презентация на тему Поле чудес Галилео Галилей  УФ-спектроскопия. Часть 1
УФ-спектроскопия. Часть 1 Лекция 4
Лекция 4 Влажность воздуха. Способы определения влажности воздуха
Влажность воздуха. Способы определения влажности воздуха Абсолютные и относительные величины
Абсолютные и относительные величины Презентация на тему Однофазный мостовой выпрямитель
Презентация на тему Однофазный мостовой выпрямитель  Термоядерный реактор. Безопасная энергия
Термоядерный реактор. Безопасная энергия Оптика и механика. Физика для химиков. День пятый
Оптика и механика. Физика для химиков. День пятый Оптимизация системы ремонта и технического обслуживания (ТО) электродвигателей системы СТД
Оптимизация системы ремонта и технического обслуживания (ТО) электродвигателей системы СТД Новые вспенинные и волокнистые композиционные материалы
Новые вспенинные и волокнистые композиционные материалы Резисторы и Реостаты. Занятие 7
Резисторы и Реостаты. Занятие 7 Законы Ньютона. Закон всемирного тяготения. Сила тяжести. Космические скорости
Законы Ньютона. Закон всемирного тяготения. Сила тяжести. Космические скорости Понятие о машинах и механизмах
Понятие о машинах и механизмах