Содержание
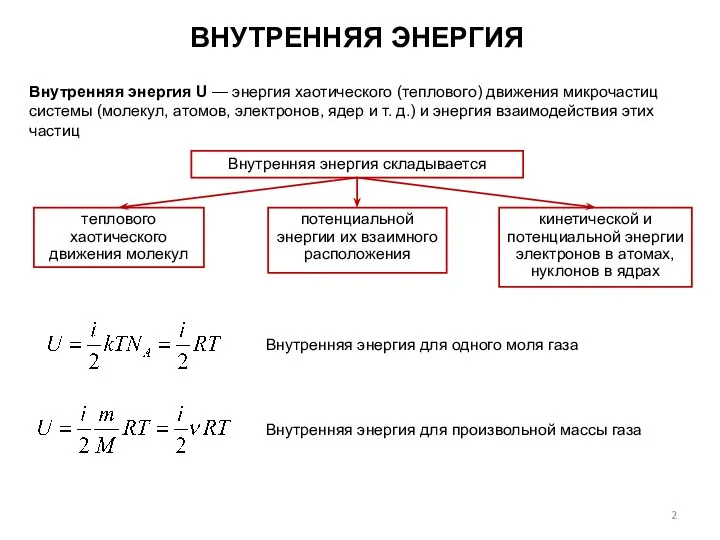
- 2. ВНУТРЕННЯЯ ЭНЕРГИЯ Внутренняя энергия U — энергия хаотического (теплового) движения микрочастиц системы (молекул, атомов, электронов, ядер
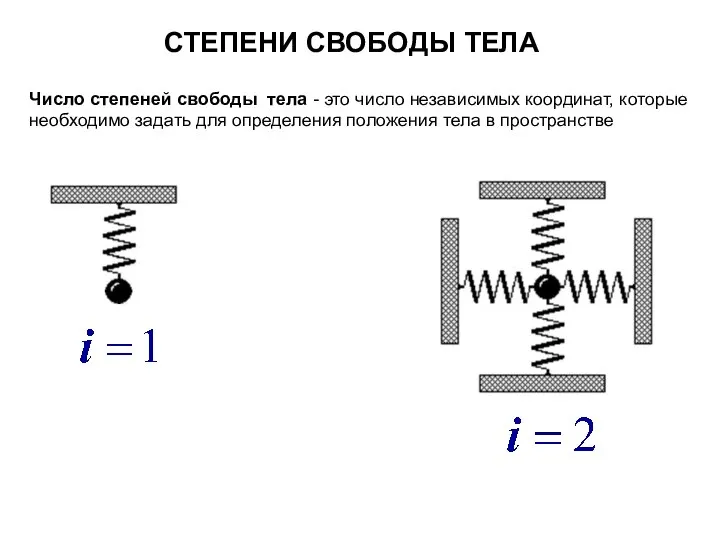
- 3. СТЕПЕНИ СВОБОДЫ ТЕЛА Число степеней свободы тела - это число независимых координат, которые необходимо задать для
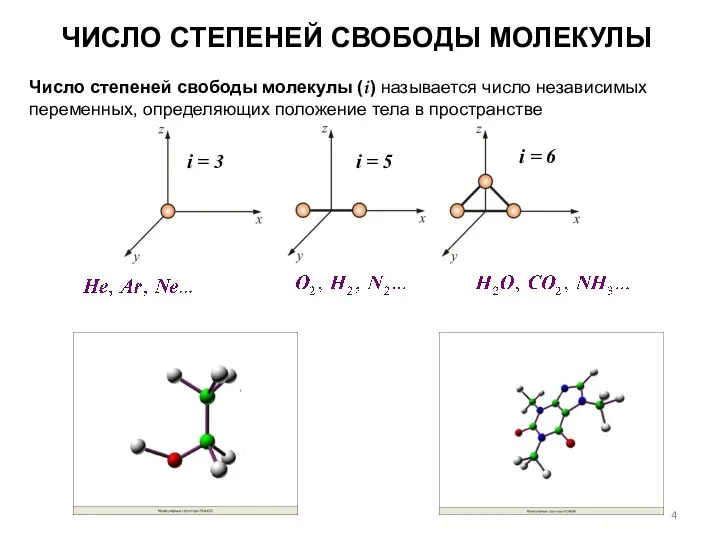
- 4. ЧИСЛО СТЕПЕНЕЙ СВОБОДЫ МОЛЕКУЛЫ Число степеней свободы молекулы (i) называется число независимых переменных, определяющих положение тела
- 5. ЧИСЛО СТЕПЕНЕЙ СВОБОДЫ МОЛЕКУЛЫ Больцман доказал, что, средняя энергия, приходящаяся на каждую степень свободы равна Для
- 6. ВНУТРЕННЯЯ ЭНЕРГИЯ ИДЕАЛЬНОГО ГАЗА Внутренняя энергия идеального газа – это кинетическая энергия движения его молекул
- 7. ПЕРВОЕ НАЧАЛО ТЕРМОДИНАМИКИ Термодинамическая система Механическая энергия = const Внутренняя энергия - изменяется совершения над системой
- 8. В каждом состоянии система обладает определенным значением внутренней энергии, поэтому можно записать ПЕРВОЕ НАЧАЛО ТЕРМОДИНАМИКИ газ,
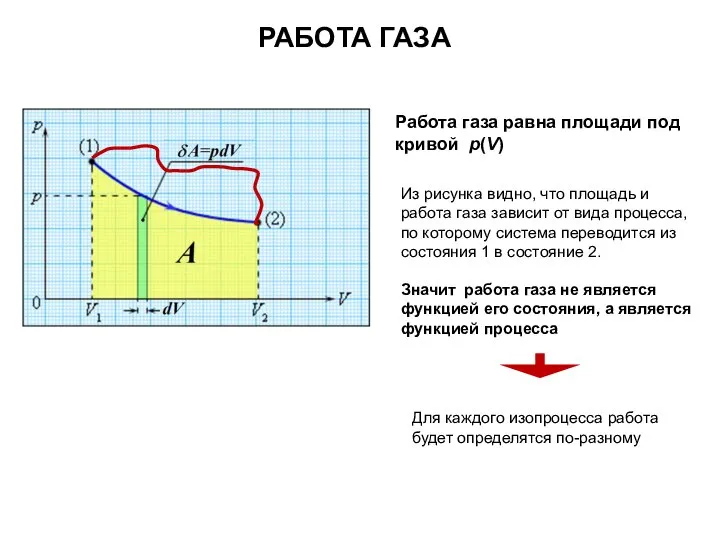
- 9. Работа газа равна площади под кривой p(V) РАБОТА ГАЗА Из рисунка видно, что площадь и работа
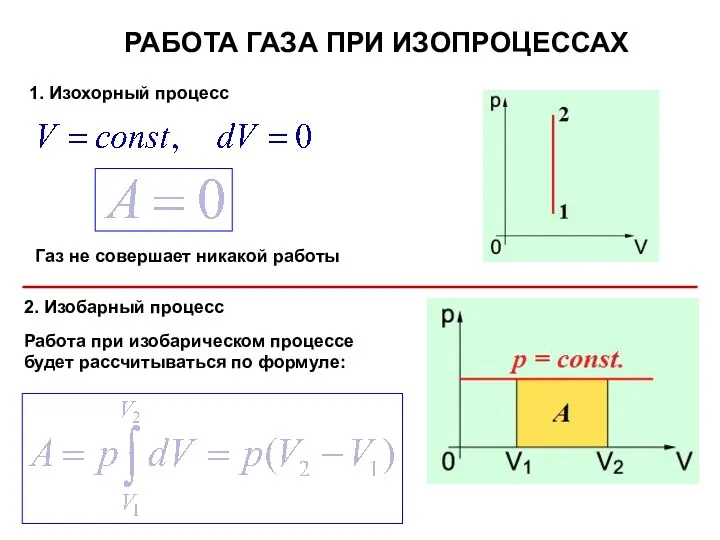
- 10. РАБОТА ГАЗА ПРИ ИЗОПРОЦЕССАХ 1. Изохорный процесс 2. Изобарный процесс Газ не совершает никакой работы Работа
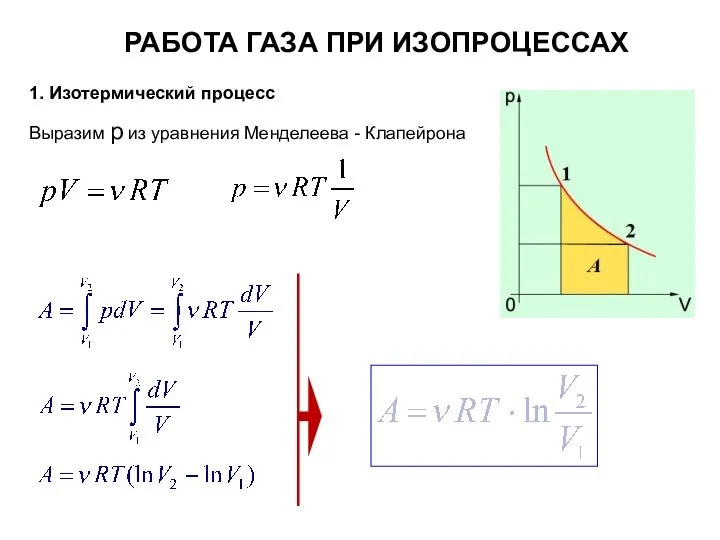
- 11. РАБОТА ГАЗА ПРИ ИЗОПРОЦЕССАХ 1. Изотермический процесс Выразим р из уравнения Менделеева - Клапейрона
- 12. КОЛИЧЕСТВО ТЕПЛОТЫ Количество теплоты Q - это величина энергии теплового движения молекул, переданной от одного тела
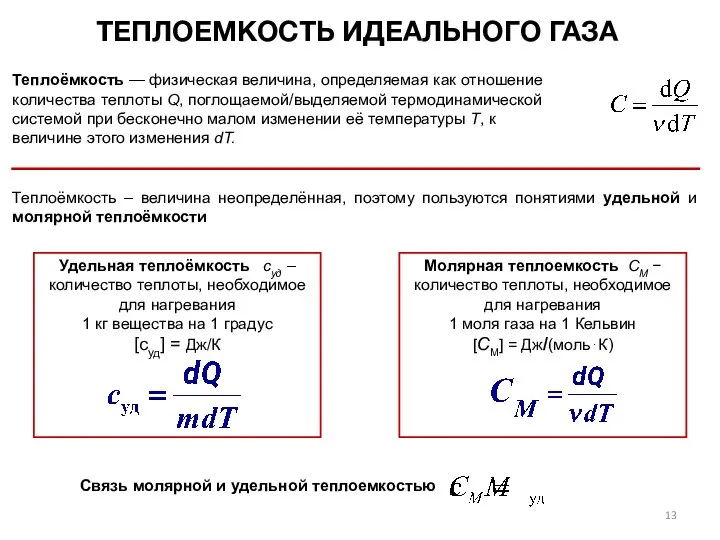
- 13. ТЕПЛОЕМКОСТЬ ИДЕАЛЬНОГО ГАЗА Теплоёмкость – величина неопределённая, поэтому пользуются понятиями удельной и молярной теплоёмкости Удельная теплоёмкость
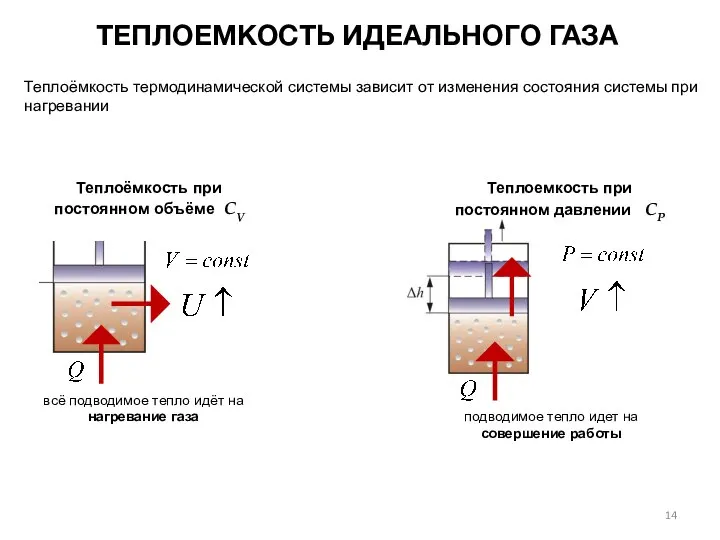
- 14. Теплоёмкость термодинамической системы зависит от изменения состояния системы при нагревании ТЕПЛОЕМКОСТЬ ИДЕАЛЬНОГО ГАЗА Теплоёмкость при постоянном
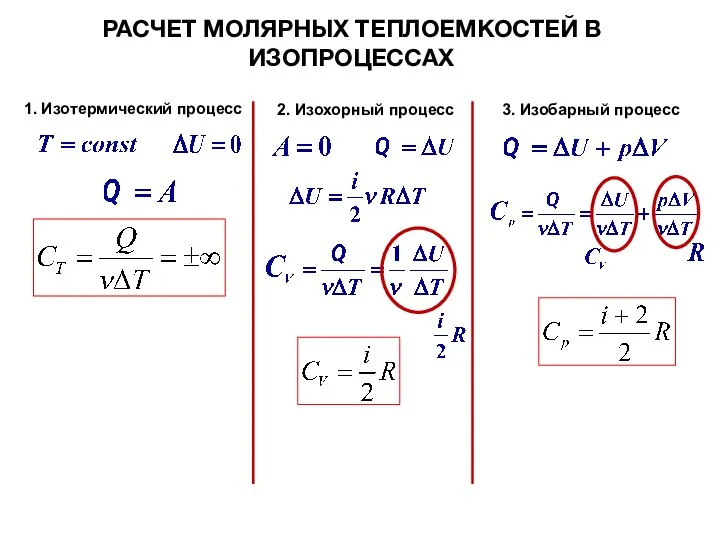
- 15. РАСЧЕТ МОЛЯРНЫХ ТЕПЛОЕМКОСТЕЙ В ИЗОПРОЦЕССАХ 1. Изотермический процесс 2. Изохорный процесс 3. Изобарный процесс
- 16. ТЕПЛОЕМКОСТЬ ИДЕАЛЬНОГО ГАЗА уравнение Майера для одного моля газа Юлиус Роберт фон Майер немецкий физик (1814
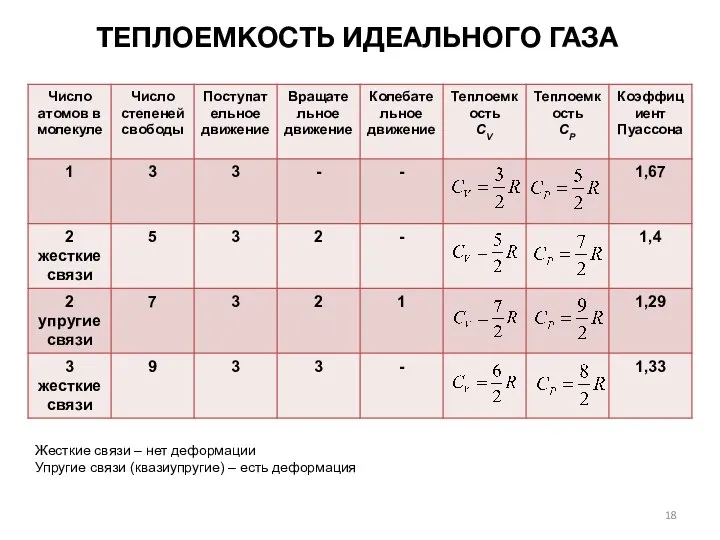
- 17. ТЕПЛОЕМКОСТЬ ИДЕАЛЬНОГО ГАЗА Из опыта с двухатомными газами Из опыта с многоатомными газами Молекулы многоатомных газов
- 18. ТЕПЛОЕМКОСТЬ ИДЕАЛЬНОГО ГАЗА Жесткие связи – нет деформации Упругие связи (квазиупругие) – есть деформация
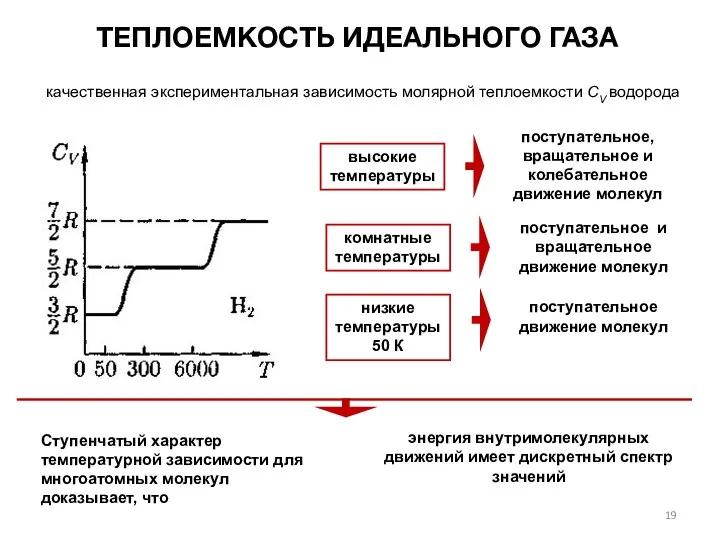
- 19. ТЕПЛОЕМКОСТЬ ИДЕАЛЬНОГО ГАЗА качественная экспериментальная зависимость молярной теплоемкости СV водорода энергия внутримолекулярных движений имеет дискретный спектр
- 20. dQ = 0 ПРИМЕНЕНИЕ ПЕРВОГО НАЧАЛА ТЕРМОДИНАМИКИ К ИЗОПРОЦЕССАМ ИДЕАЛЬНЫХ ГАЗОВ
- 21. ПРИМЕНЕНИЕ ПЕРВОГО НАЧАЛА ТЕРМОДИНАМИКИ К ИЗОПРОЦЕССАМ ИДЕАЛЬНЫХ ГАЗОВ
- 22. ПРИМЕНЕНИЕ ПЕРВОГО НАЧАЛА ТЕРМОДИНАМИКИ К ИЗОПРОЦЕССАМ ИДЕАЛЬНЫХ ГАЗОВ
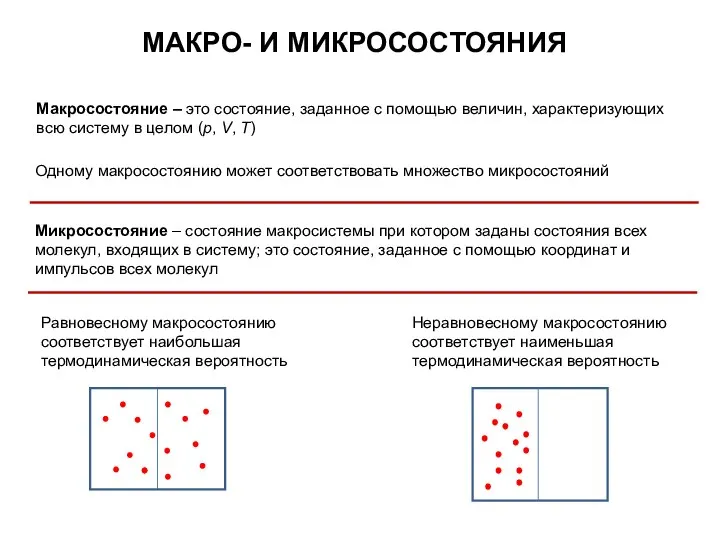
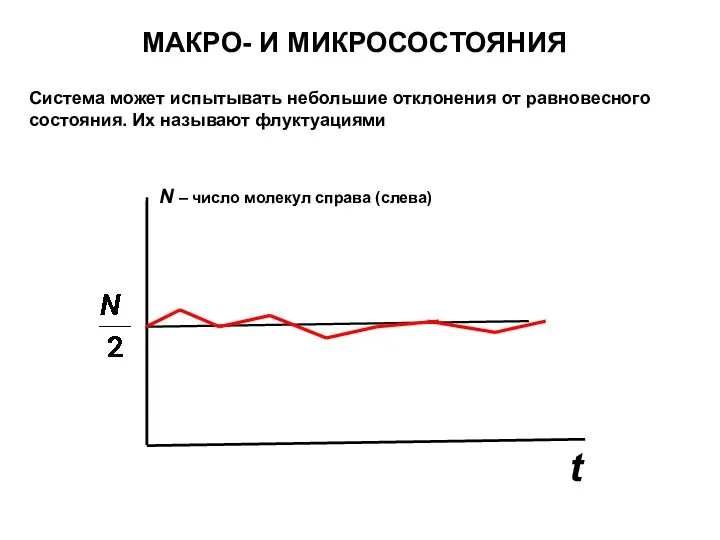
- 23. МАКРО- И МИКРОСОСТОЯНИЯ Макросостояние – это состояние, заданное с помощью величин, характеризующих всю систему в целом
- 24. Система может испытывать небольшие отклонения от равновесного состояния. Их называют флуктуациями t N – число молекул
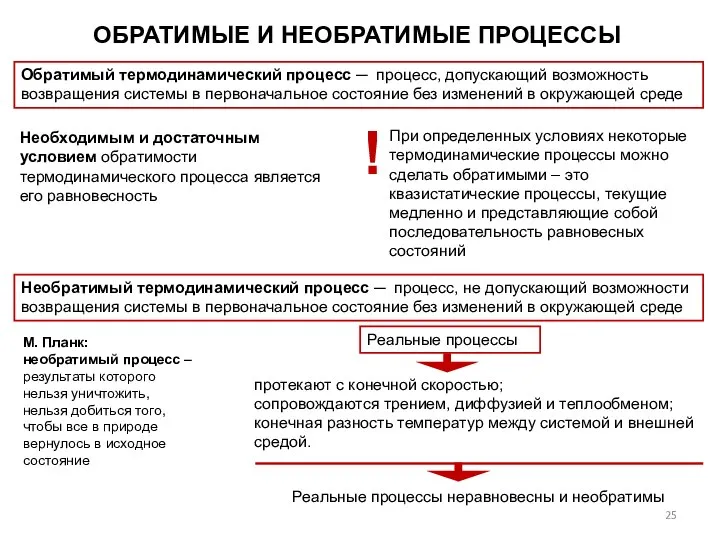
- 25. ОБРАТИМЫЕ И НЕОБРАТИМЫЕ ПРОЦЕССЫ Обратимый термодинамический процесс ─ процесс, допускающий возможность возвращения системы в первоначальное состояние
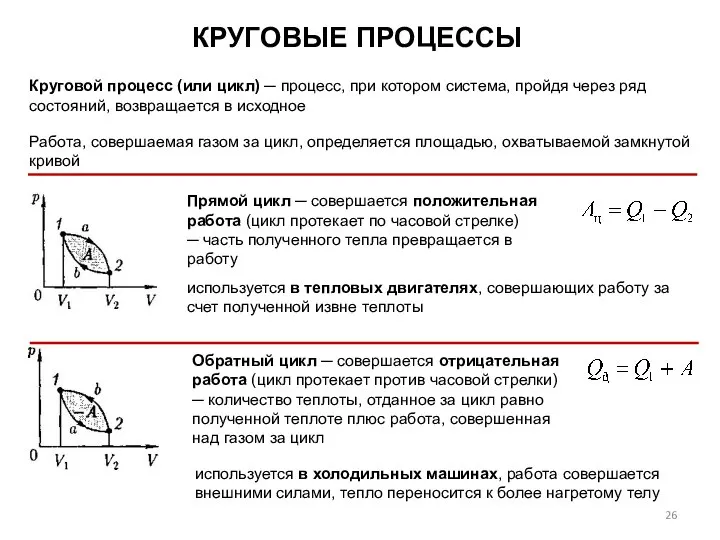
- 26. КРУГОВЫЕ ПРОЦЕССЫ Обратный цикл ─ совершается отрицательная работа (цикл протекает против часовой стрелки) ─ количество теплоты,
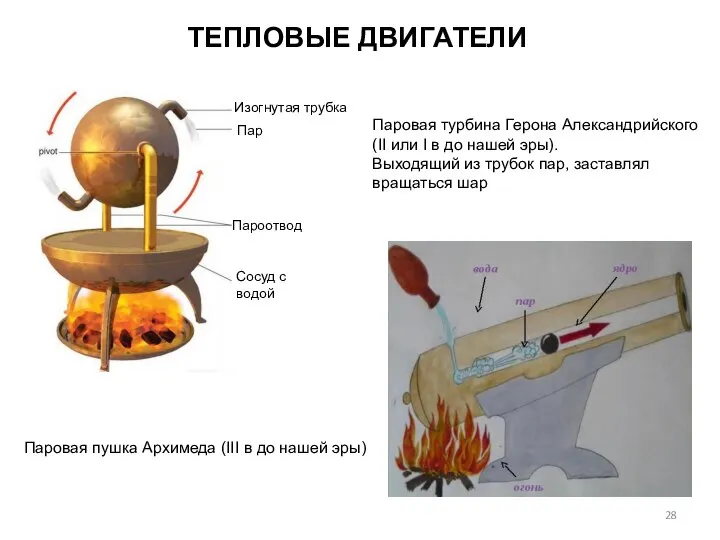
- 27. ТЕПЛОВЫЕ ДВИГАТЕЛИ В нагревателе происходит сгорание топлива, выделяется количество теплоты Q1, нагреватель при этом нагревается до
- 28. Паровая турбина Герона Александрийского (II или I в до нашей эры). Выходящий из трубок пар, заставлял
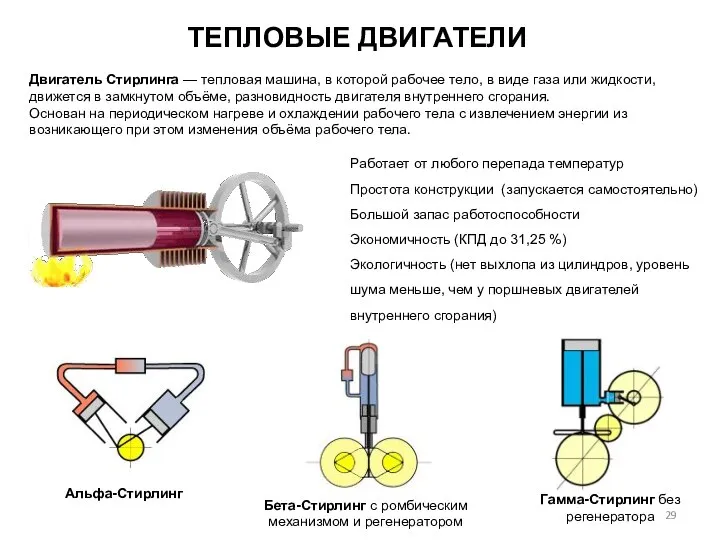
- 29. Двигатель Стирлинга — тепловая машина, в которой рабочее тело, в виде газа или жидкости, движется в
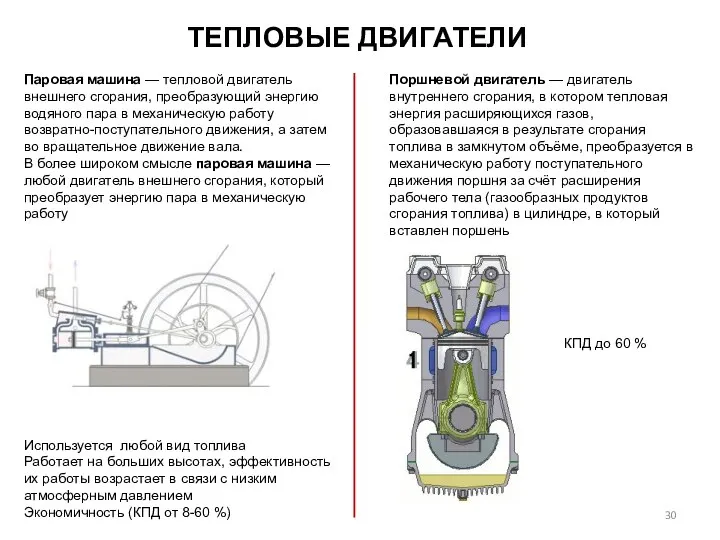
- 30. Паровая машина — тепловой двигатель внешнего сгорания, преобразующий энергию водяного пара в механическую работу возвратно-поступательного движения,
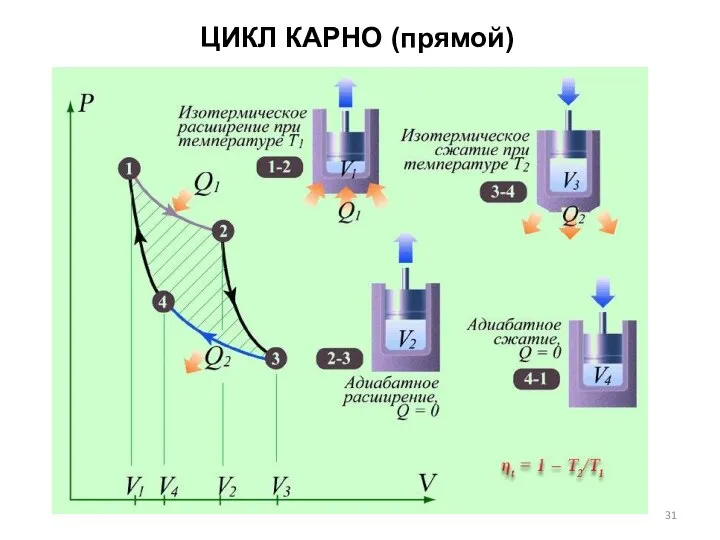
- 31. ЦИКЛ КАРНО (прямой)
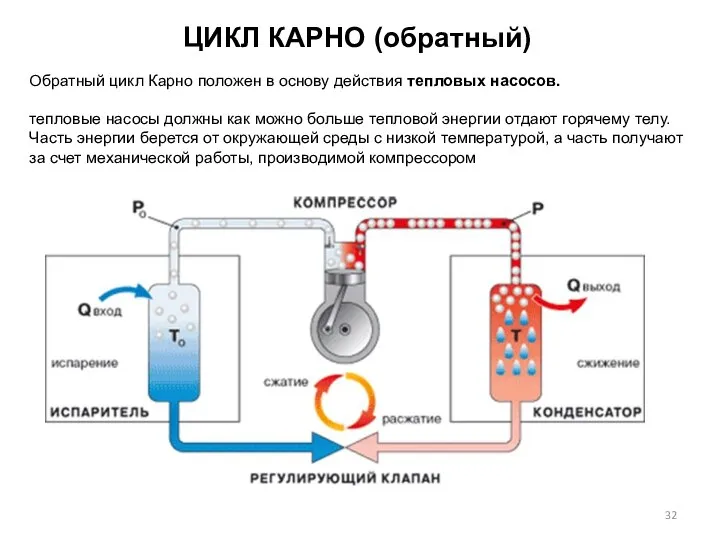
- 32. ЦИКЛ КАРНО (обратный) Обратный цикл Карно положен в основу действия тепловых насосов. тепловые насосы должны как
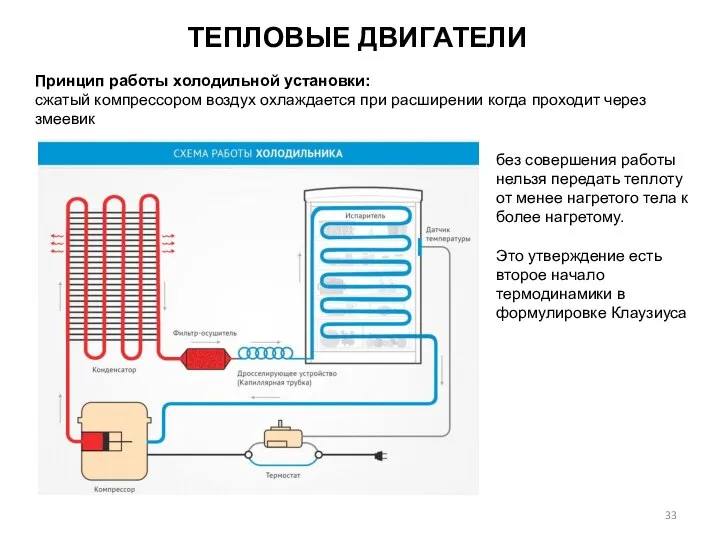
- 33. ТЕПЛОВЫЕ ДВИГАТЕЛИ без совершения работы нельзя передать теплоту от менее нагретого тела к более нагретому. Это
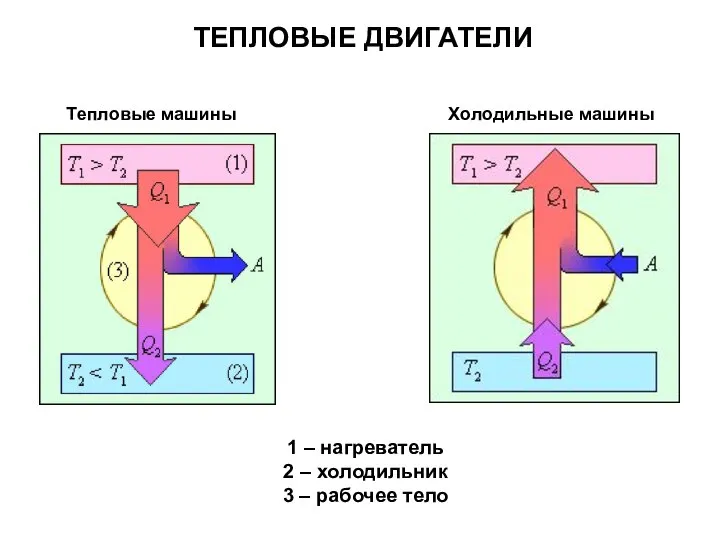
- 34. Тепловые машины 1 – нагреватель 2 – холодильник 3 – рабочее тело ТЕПЛОВЫЕ ДВИГАТЕЛИ Холодильные машины
- 35. ОБРАТИМЫЕ И НЕОБРАТИМЫЕ ПРОЦЕССЫ В результате кругового процесса система возвращается в исходное состояние и полное изменение
- 36. ЭНТРОПИЯ Рудольф Клаузиус немецкий физик (1822 – 1888) Из цикла Карно следует, что равны между собой
- 37. ЭНТРОПИЯ Для обратимых процессов в замкнутой системе изменение энтропии это выражение называется равенством Клаузиуса Неравенство Клаузиуса
- 38. ЭНТРОПИЯ
- 39. Свободная энергия Гиббса (или просто энергия Гиббса, или потенциал Гиббса, или термодинамический потенциал в узком смысле)
- 40. Все реальные тепловые процессы протекают с увеличением энтропии, то есть устанавливается тепловое равновесие упорядоченность в окружающем
- 41. ВТОРОЕ НАЧАЛО ТЕРМОДИНАМИКИ Второе начало термодинамики можно сформулировать как закон возрастания энтропии замкнутой системы при необратимых
- 42. ТРЕТЬЕ НАЧАЛО ТЕРМОДИНАМИКИ На основании обобщения экспериментальных исследований свойств веществ при сверхнизких температурах был установлен закон
- 43. ФАЗОВЫЕ ПЕРЕХОДЫ ПЕРВОГО И ВТОРОГО РОДА Фаза - термодинамически равновесное состояние вещества, отличающееся от других возможных
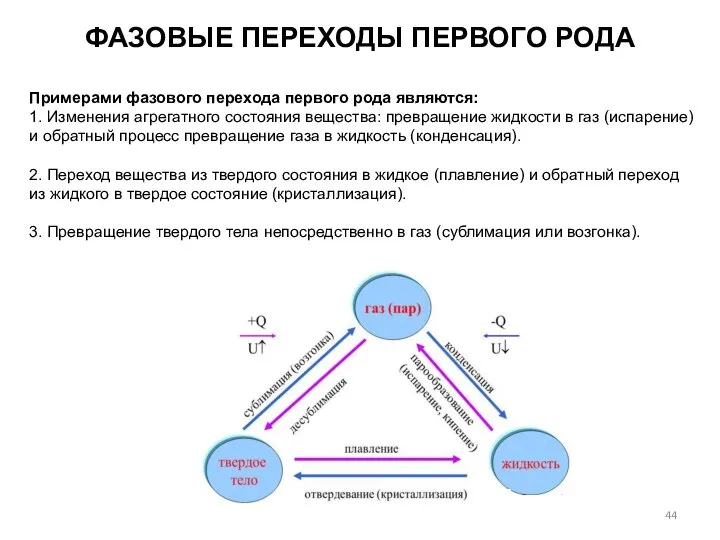
- 44. ФАЗОВЫЕ ПЕРЕХОДЫ ПЕРВОГО РОДА Примерами фазового перехода первого рода являются: 1. Изменения агрегатного состояния вещества: превращение
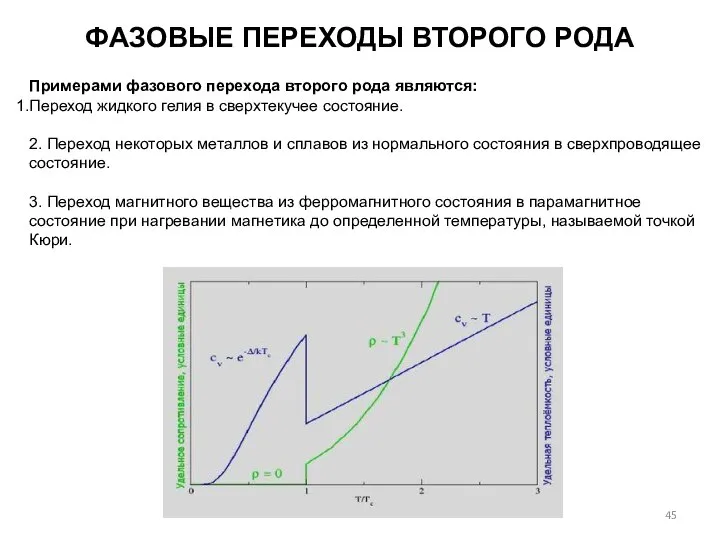
- 45. ФАЗОВЫЕ ПЕРЕХОДЫ ВТОРОГО РОДА Примерами фазового перехода второго рода являются: Переход жидкого гелия в сверхтекучее состояние.
- 46. ФАЗОВЫЕ ПРЕВРАЩЕНИЯ Фазовые превращения ‒ это переход вещества из одной фазы в другую, связанный с качественными
- 47. Фазовый переход «твердое тело – жидкость» 1.Переход вещества из твердого состояния (фазы) в жидкое называется плавлением,
- 48. Фазовый переход «жидкость – газ» 1. Переход вещества из жидкости в газовую фазу называется испарением, а
- 49. Если система однокомпонентная, т.е. состоит из химически однородного вещества, то понятие фазы совпадает с понятием агрегатного
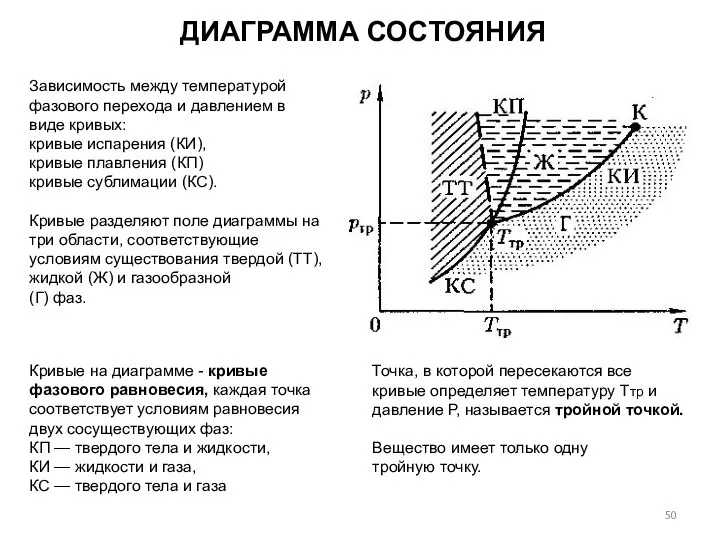
- 50. Зависимость между температурой фазового перехода и давлением в виде кривых: кривые испарения (КИ), кривые плавления (КП)
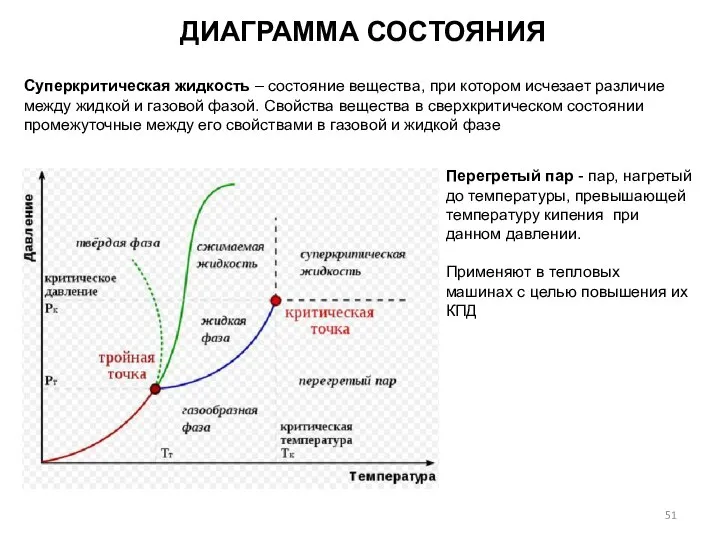
- 51. ДИАГРАММА СОСТОЯНИЯ Суперкритическая жидкость – состояние вещества, при котором исчезает различие между жидкой и газовой фазой.
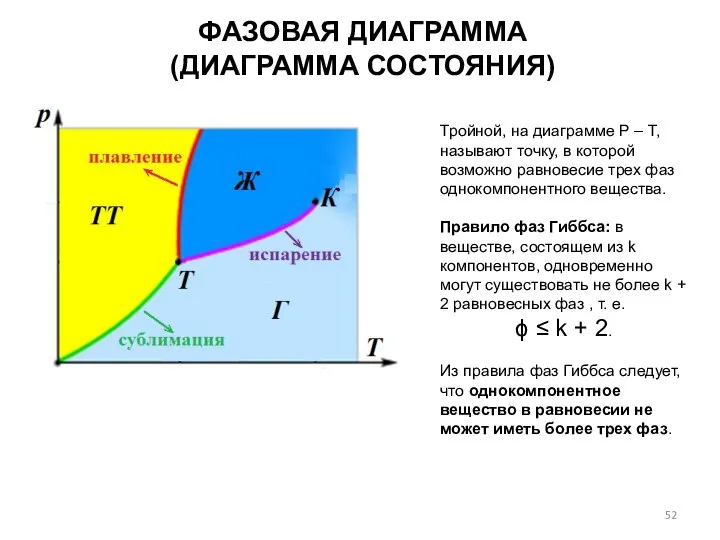
- 52. ФАЗОВАЯ ДИАГРАММА (ДИАГРАММА СОСТОЯНИЯ) Тройной, на диаграмме Р – Т, называют точку, в которой возможно равновесие
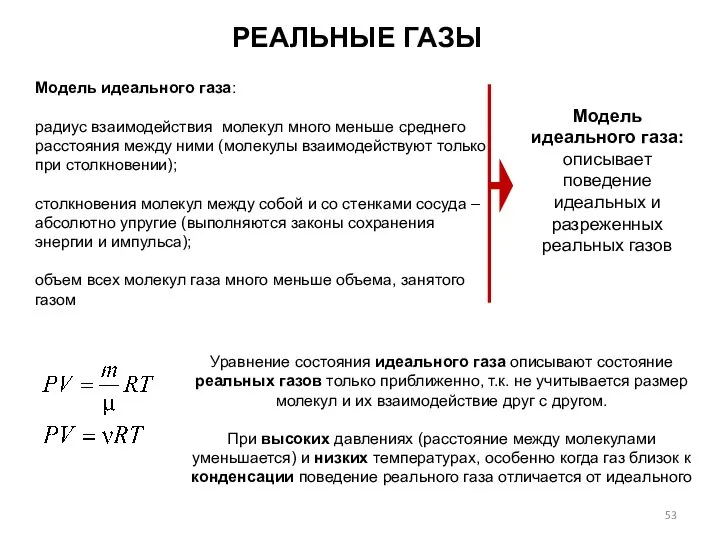
- 53. РЕАЛЬНЫЕ ГАЗЫ Модель идеального газа: радиус взаимодействия молекул много меньше среднего расстояния между ними (молекулы взаимодействуют
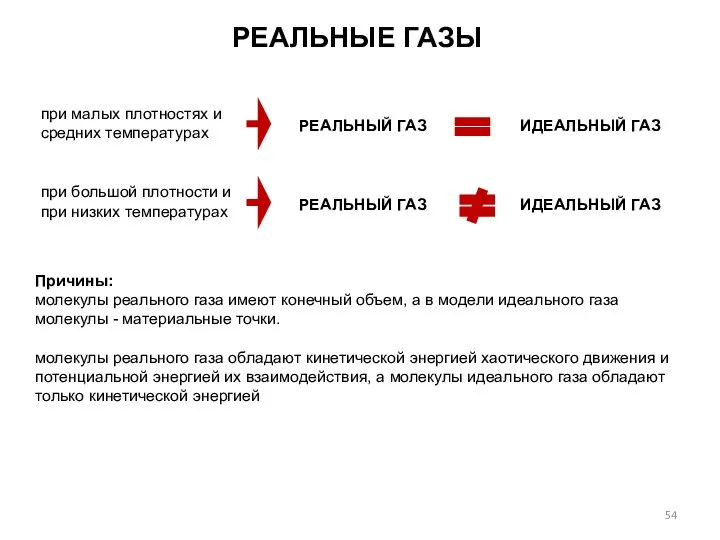
- 54. РЕАЛЬНЫЕ ГАЗЫ при малых плотностях и средних температурах РЕАЛЬНЫЙ ГАЗ при большой плотности и при низких
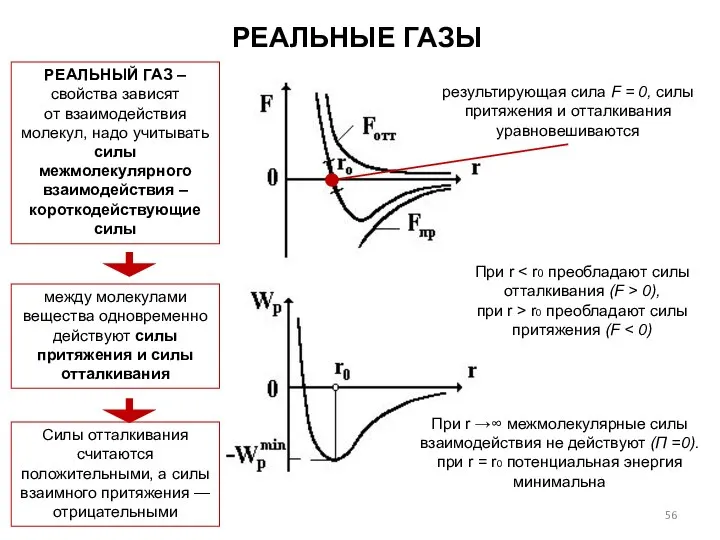
- 55. РЕАЛЬНЫЕ ГАЗЫ Реальные газы – газы, свойства которых зависят от взаимодействия молекул Силы межмолекулярного взаимодействия. Они
- 56. РЕАЛЬНЫЕ ГАЗЫ РЕАЛЬНЫЙ ГАЗ – свойства зависят от взаимодействия молекул, надо учитывать силы межмолекулярного взаимодействия –
- 57. РЕАЛЬНЫЕ ГАЗЫ Йоханнес Дидерик Ван-дер-Ваальс голландский физик (1837 – 1923) Газом Ван-дер-Ваальса называется модель реального газа,
- 58. РЕАЛЬНЫЕ ГАЗЫ Основное отличие реального газа от идеального: идеальный газ нельзя перевести в жидкое состояние ни
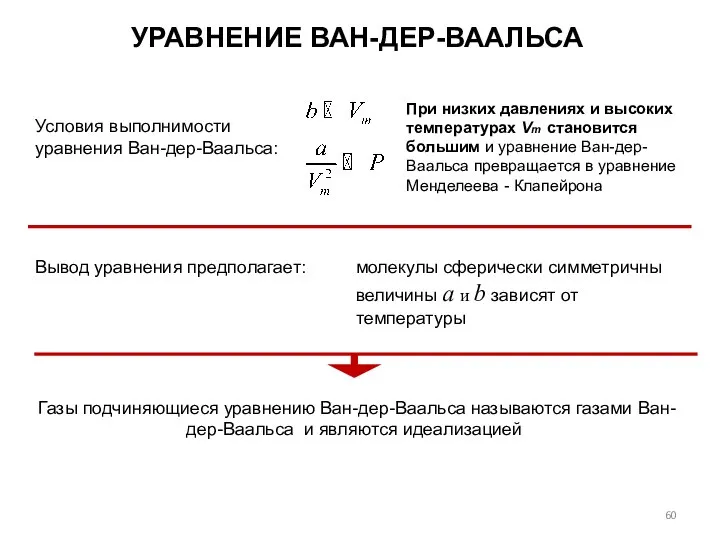
- 59. УРАВНЕНИЕ ВАН-ДЕР-ВААЛЬСА Уравнение Ван-дер-Ваальса для 1 киломоля газа (уравнение состояния реальных газов) Уравнение учитывает конечные размеры
- 60. УРАВНЕНИЕ ВАН-ДЕР-ВААЛЬСА Условия выполнимости уравнения Ван-дер-Ваальса: Вывод уравнения предполагает: молекулы сферически симметричны величины а и b
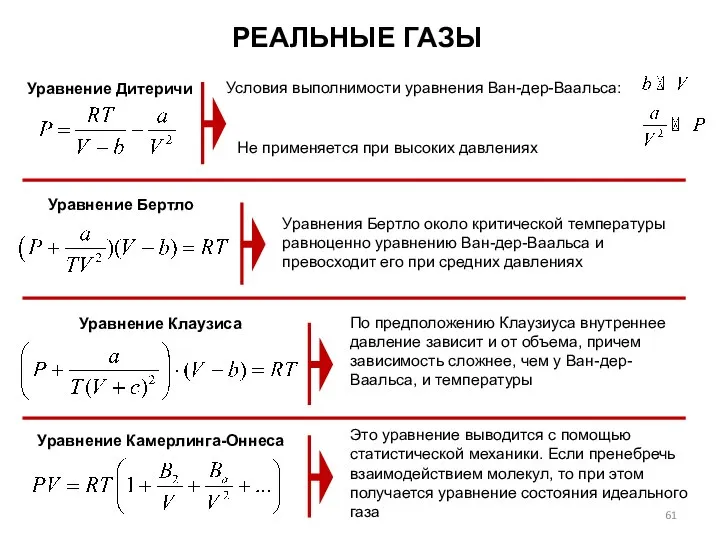
- 61. РЕАЛЬНЫЕ ГАЗЫ Уравнение Дитеричи Условия выполнимости уравнения Ван-дер-Ваальса: Уравнения Бертло около критической температуры равноценно уравнению Ван-дер-Ваальса
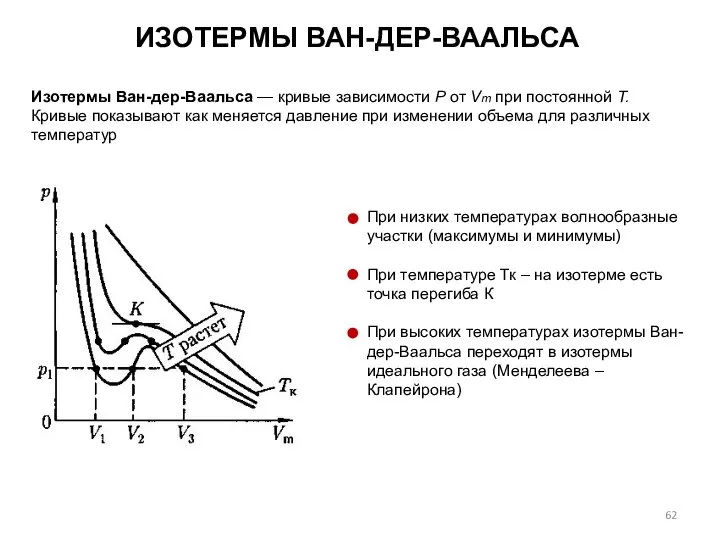
- 62. ИЗОТЕРМЫ ВАН-ДЕР-ВААЛЬСА Изотермы Ван-дер-Ваальса — кривые зависимости Р от Vm при постоянной Т. Кривые показывают как
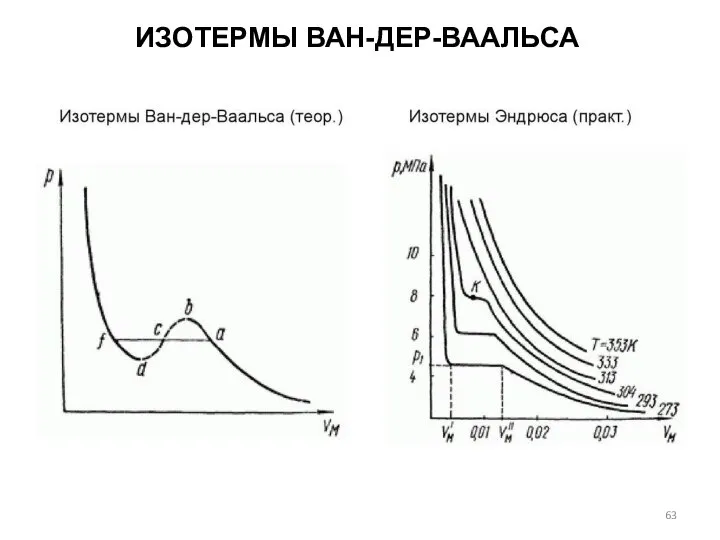
- 63. ИЗОТЕРМЫ ВАН-ДЕР-ВААЛЬСА
- 64. ИЗОТЕРМЫ ВАН-ДЕР-ВААЛЬСА В 1866 г. экспериментально исследовал зависимость молярного объема Vm углекислого газа от давления при
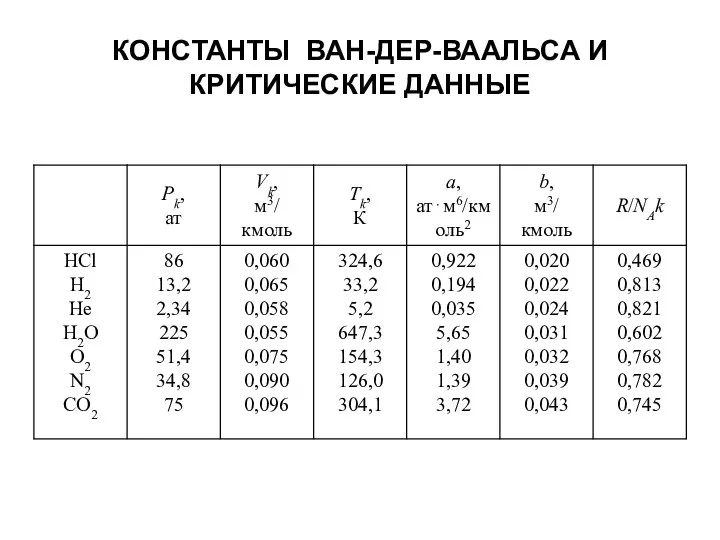
- 65. КОНСТАНТЫ ВАН-ДЕР-ВААЛЬСА И КРИТИЧЕСКИЕ ДАННЫЕ
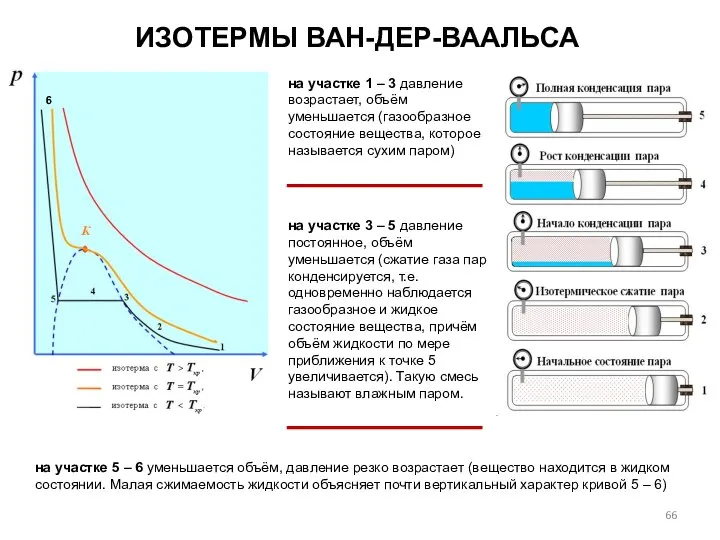
- 66. ИЗОТЕРМЫ ВАН-ДЕР-ВААЛЬСА на участке 1 – 3 давление возрастает, объём уменьшается (газообразное состояние вещества, которое называется
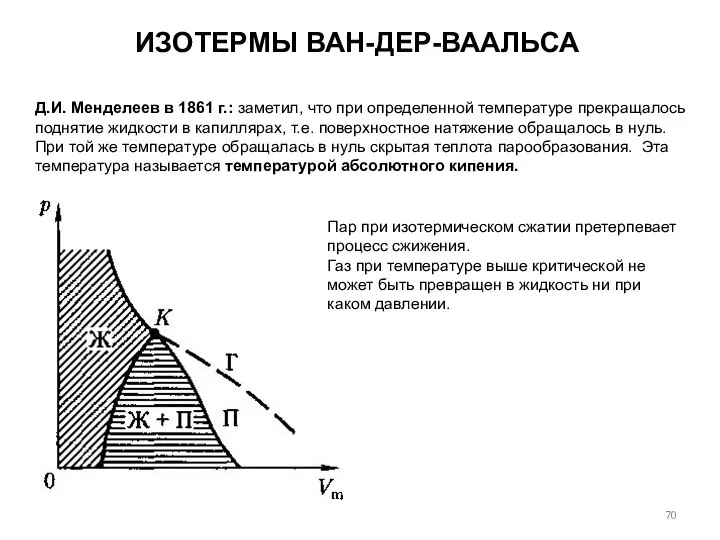
- 67. Газ при температуре выше критической не может быть превращен в жидкость ни при каком давлении. ИЗОТЕРМЫ
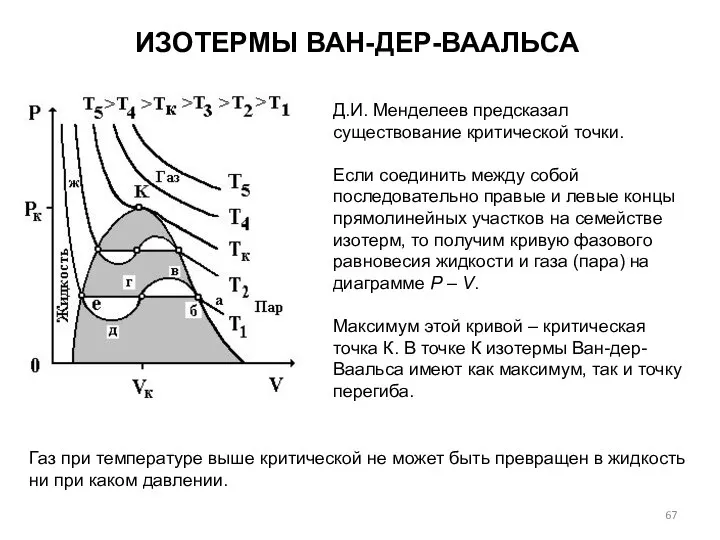
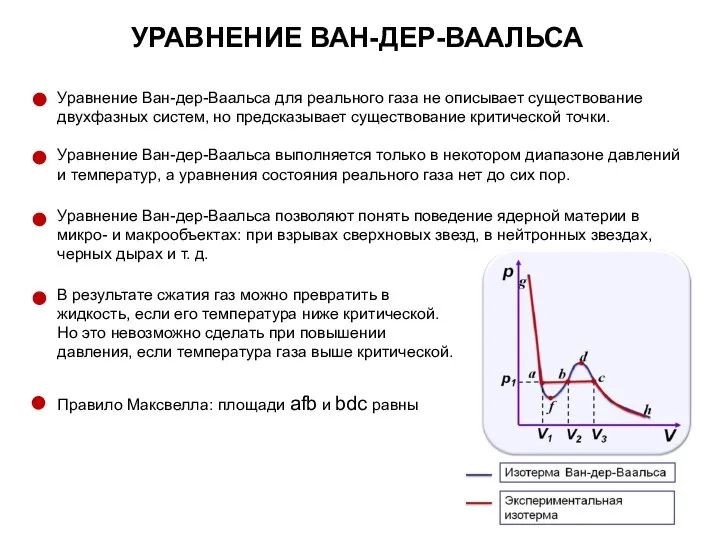
- 68. УРАВНЕНИЕ ВАН-ДЕР-ВААЛЬСА Уравнение Ван-дер-Ваальса для реального газа не описывает существование двухфазных систем, но предсказывает существование критической
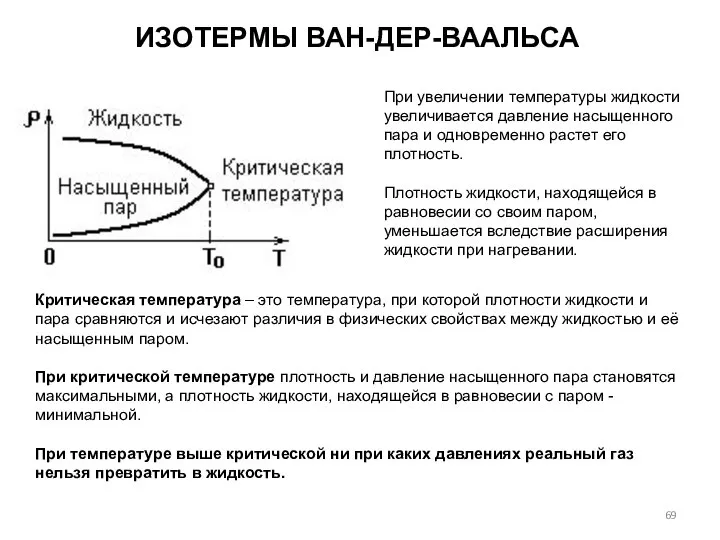
- 69. ИЗОТЕРМЫ ВАН-ДЕР-ВААЛЬСА При увеличении температуры жидкости увеличивается давление насыщенного пара и одновременно растет его плотность. Плотность
- 70. Д.И. Менделеев в 1861 г.: заметил, что при определенной температуре прекращалось поднятие жидкости в капиллярах, т.е.
- 71. Внутренняя энергия одного моля газа Ван-дер-Ваальса (реального газа) складывается из: кинетической энергии теплового движения молекул потенциальной
- 72. при адиабатном расширении без совершения внешней работы внутренняя энергия газа не изменяется Равенство справедливо как для
- 73. ЭФФЕКТ ДЖОУЛЯ-ТОМСОНА Идеальный газ адиабатно расширяется и совершает работу - газ охлаждается, так как работа совершается
- 74. Совершенная над газом результирующая внешняя работа равна В адиабатических внешних условиях эта работа идет на изменение
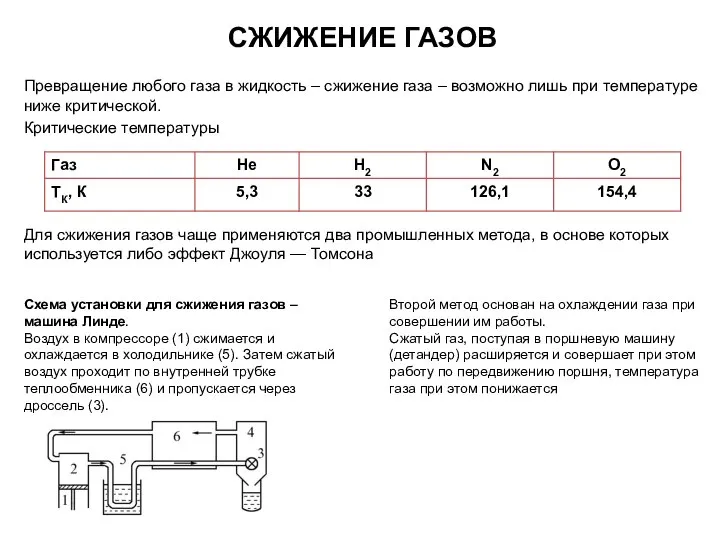
- 75. Превращение любого газа в жидкость – сжижение газа – возможно лишь при температуре ниже критической. Критические
- 77. Скачать презентацию
































 Механическая работа. Мощность
Механическая работа. Мощность Состав и строение атома
Состав и строение атома Ядерные реакции под действием нейтронов. (Тема 2.6)
Ядерные реакции под действием нейтронов. (Тема 2.6) Тема урока: Магнитное поле катушки с током. Электромагнит. Цель урока: исследовать зависимость силы магнитного поля катушки с токо
Тема урока: Магнитное поле катушки с током. Электромагнит. Цель урока: исследовать зависимость силы магнитного поля катушки с токо Назначение основных размеров опор и определение нагрузок, действующих на опоры
Назначение основных размеров опор и определение нагрузок, действующих на опоры Фотоэффект
Фотоэффект Мир вокруг нас
Мир вокруг нас Квантовая биофизика
Квантовая биофизика Движение тела по окружности с постоянной по модулю скоростью
Движение тела по окружности с постоянной по модулю скоростью Презентация на тему Электробезопасность
Презентация на тему Электробезопасность  Измерение cилы трения
Измерение cилы трения Задача №16 Магнитная пушка
Задача №16 Магнитная пушка Сиракузы. III век до нашей эры
Сиракузы. III век до нашей эры Основные понятия теории механизмов и машин
Основные понятия теории механизмов и машин Диоды Ганна
Диоды Ганна Неравномерное движение. Мгновенная скорость
Неравномерное движение. Мгновенная скорость Последовательное соединение
Последовательное соединение Звук и его характеристики
Звук и его характеристики Разнообразие веществ в окружающем мире
Разнообразие веществ в окружающем мире Презентация на тему Деление ядер урана Атомная энергетика
Презентация на тему Деление ядер урана Атомная энергетика  Аналогово-цифровой контроллер
Аналогово-цифровой контроллер Методы наблюдения и регистрации элементарных частиц
Методы наблюдения и регистрации элементарных частиц Основные законы электрической цепи постоянного тока
Основные законы электрической цепи постоянного тока Основы квантовой физики
Основы квантовой физики Автосцепное устройство
Автосцепное устройство Воздухоплавание
Воздухоплавание Презентация на тему Молекулярная физика. Ученые и их открытия
Презентация на тему Молекулярная физика. Ученые и их открытия  Диагностика дизельных двигателей
Диагностика дизельных двигателей