Гармонические колебания

Колебания называются свободными (или собственными), если они совершаются за счет первоначально сообщенной энергии при последующем отсутствии внешних воздействий на колебательную систему (систему, совершающую колебания).
Простейшим типом колебаний являются гармонические колебания — колебания, при которых колеблющаяся величина изменяется со временем по закону синуса (косинуса).
Рассмотрение гармонических колебаний важно по двум причинам:
колебания, встречающиеся в природе и технике, часто имеют характер, близкий к гармоническому;
различные периодические процессы (процессы, повторяющиеся через равные промежутки времени) можно представить как наложение гармонических колебаний.

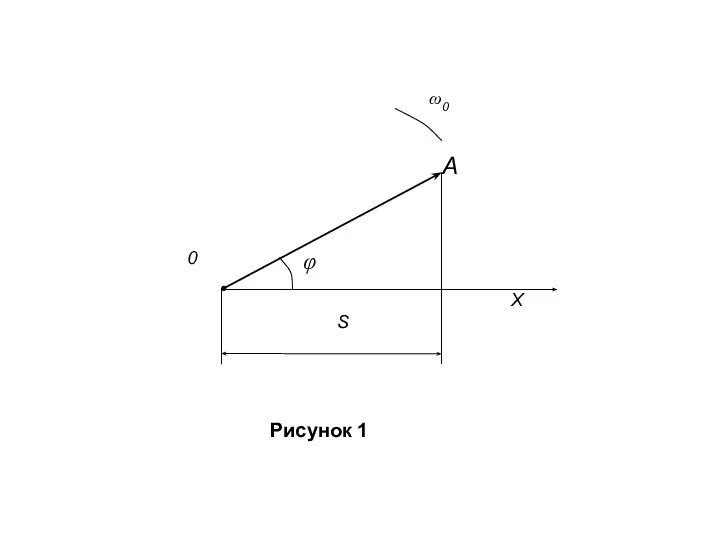
Гармонические колебания величины s описываются уравнением типа
(1)
где А максимальное значение колеблющейся величины, называемое амплитудой колебаний, - круговая (циклическая) частота, - начальная фаза колебаний в момент времени t = 0, ( ) - фаза колебаний и момент времени t. Так как косинус изменяется в пределах от +1 до -1, то s может принимать значения от +А до -А.

Определенные состояния системы, совершающей гармонические колебания, повторяются через промежуток времени Т, называемый периодом колебания, за который фаза колебания получает приращение 2π, т. е.
откуда
Величина, обратная периоду колебаний, т. е. число полных колебаний, совершаемых в единицу времени, называется частотой колебаний.

Единица частоты — герц (Гц): 1 Гц — частота периодического процесса, при которой за 1 с совершается один цикл процесса.
Запишем первую и вторую производные по времени от гармонически колеблющейся величины s (соответственно скорость и ускорение):
(2)
(3)
т. е. имеем гармонические колебания с той же циклической частотой.

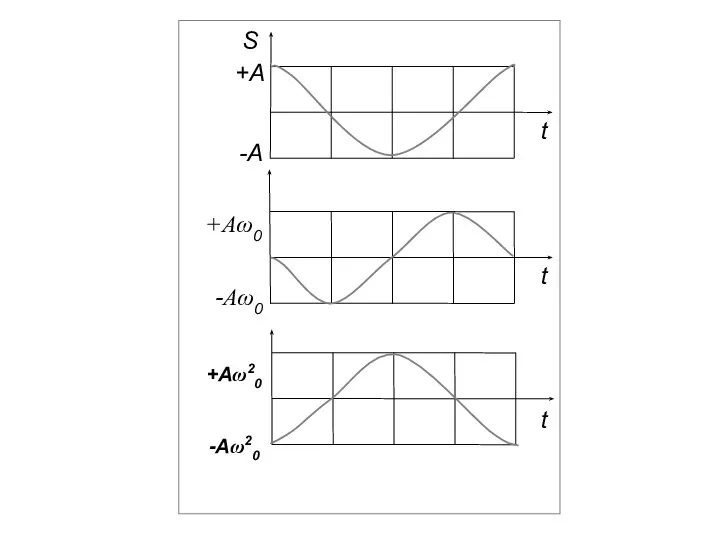
Дифференциальное уравнение гармонических колебаний имеет вид:
Решением этого уравнения является выражение (1).
Гармонические колебания изображаются (см. рис.1) графически методом вращающегося вектора амплитуды, или методом векторных диаграмм.
Если этот вектор привести во вращение с угловой скоростью , то проекция конца вектора на ось х будет будет изменяться со временем по закону .
(4)

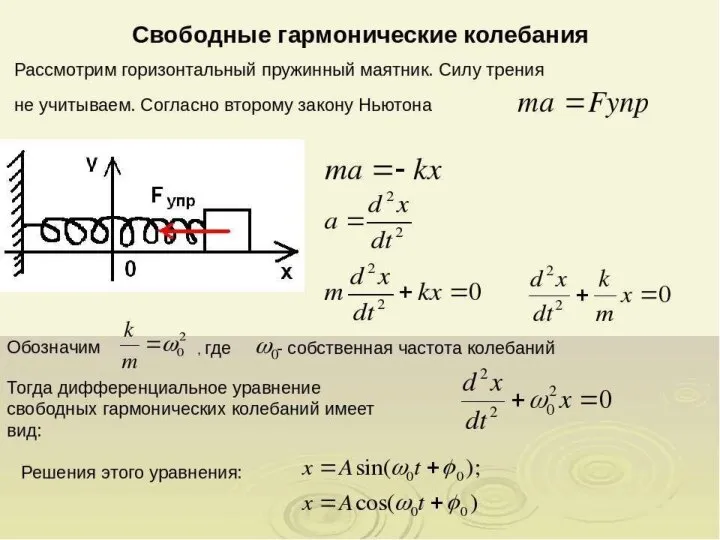
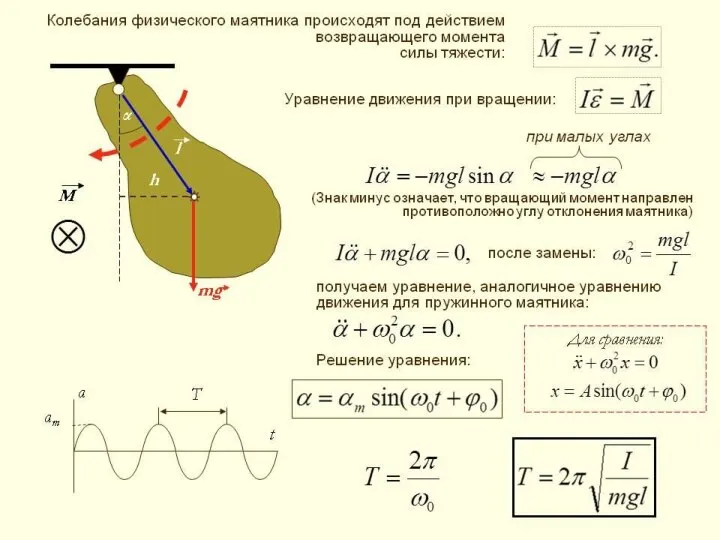
Гармонический осциллятор. Пружинный, физический и математический маятники
Гармоническим осциллятором называется система, совершающая колебания, описываемые уравнением вида:
Колебания гармонического осциллятора являются важным примером периодического движения и служат точной или приближенной моделью во многих задачах классической и квантовой физики. Примерами гармонического осциллятора являются пружинный, физический и математический маятники.

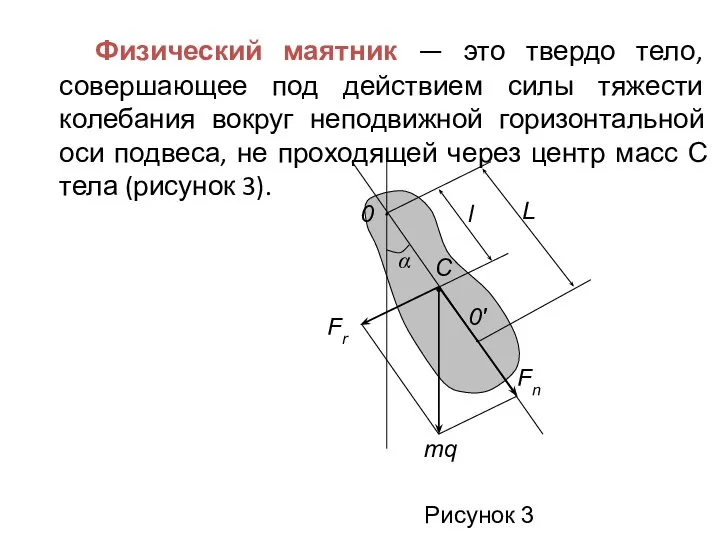
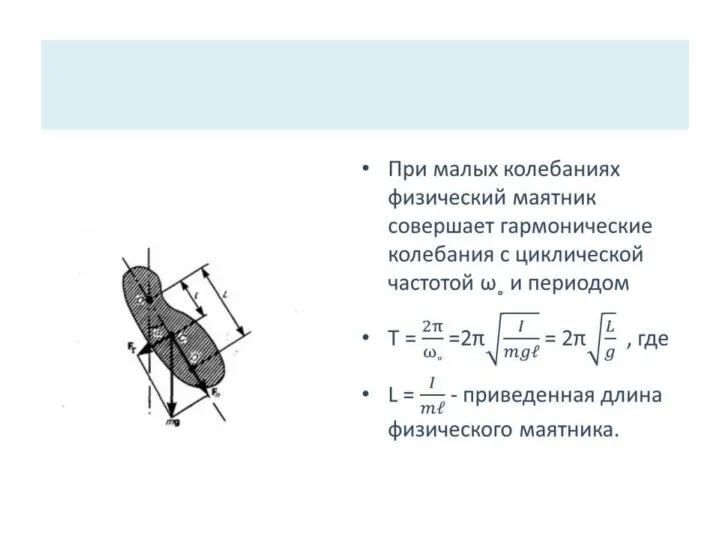
Физический маятник — это твердо тело, совершающее под действием силы тяжести колебания вокруг неподвижной горизонтальной оси подвеса, не проходящей через центр масс С тела (рисунок 3).