Содержание
- 3. 1.ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ УПРУГОЙ ДЕФОРМАЦИИ СТЕРЖНЯ 1.1 РАСТЯЖЕНИЕ ( СЖАТИЕ ) СТЕРЖНЯ Рис.а Рис. б.
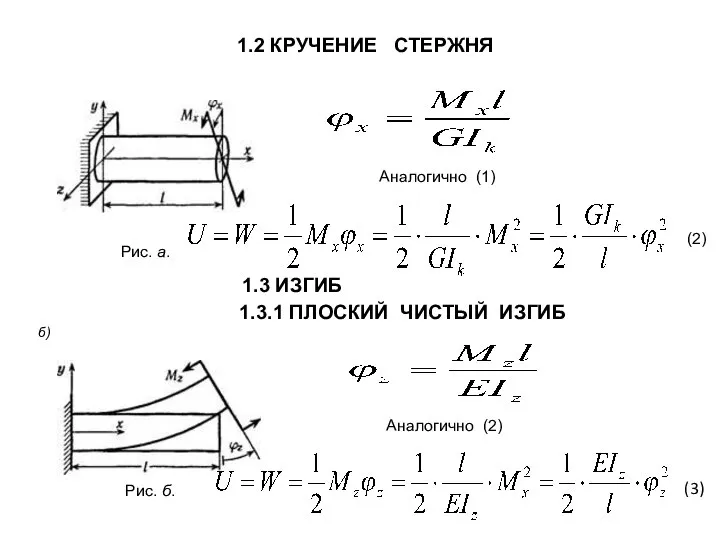
- 4. 1.2 КРУЧЕНИЕ СТЕРЖНЯ а) Аналогично (1) (2) 1.3 ИЗГИБ б) 1.3.1 ПЛОСКИЙ ЧИСТЫЙ ИЗГИБ Аналогично (2)
- 5. 1.3.2 ПЛОСКИЙ ИЗГИБ Mz(x) ≠ const. Соотношение (3) применимо к участку длинной dx Вклад в потенциальную
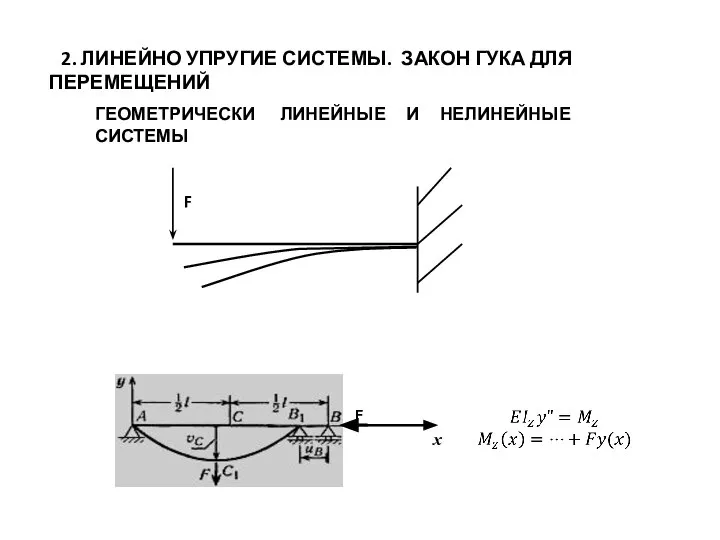
- 6. 2. ЛИНЕЙНО УПРУГИЕ СИСТЕМЫ. ЗАКОН ГУКА ДЛЯ ПЕРЕМЕЩЕНИЙ ГЕОМЕТРИЧЕСКИ ЛИНЕЙНЫЕ И НЕЛИНЕЙНЫЕ СИСТЕМЫ
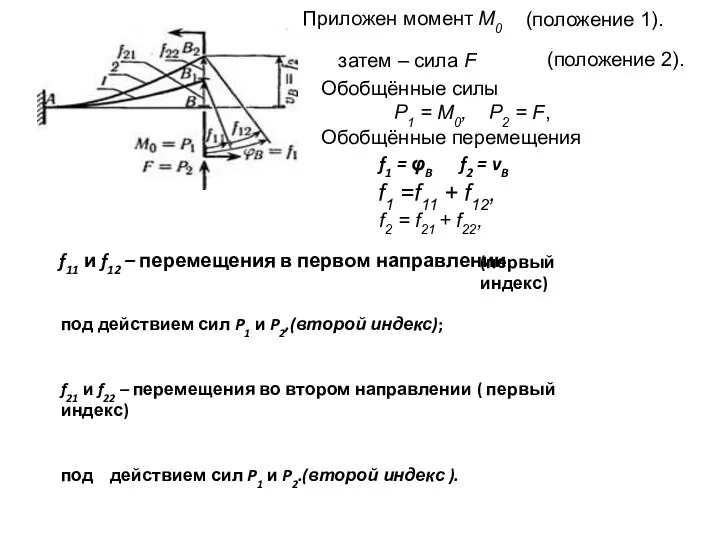
- 7. Приложен момент М0 затем – сила F (положение 1). (положение 2). Обобщённые силы P1 = M0,
- 8. Коэффициенты податливости , , , . При действии n обобщённых сил (закон Гука для перемещений) Далее
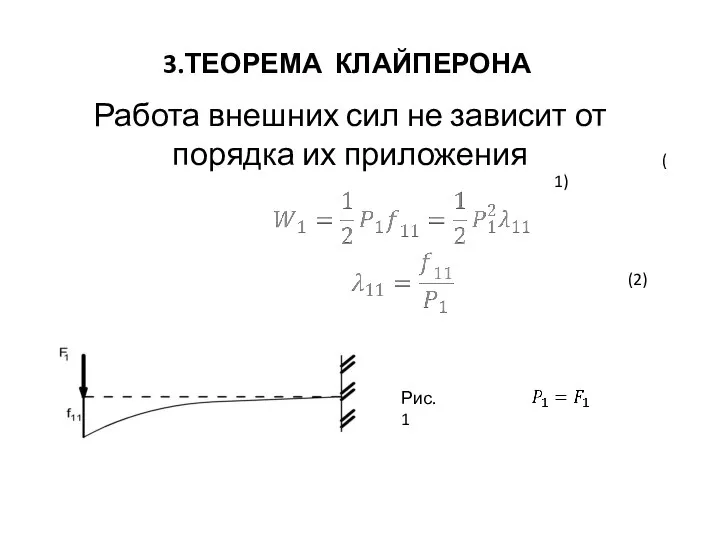
- 9. Работа внешних сил не зависит от порядка их приложения (1) (2) Рис.1 3.ТЕОРЕМА КЛАЙПЕРОНА
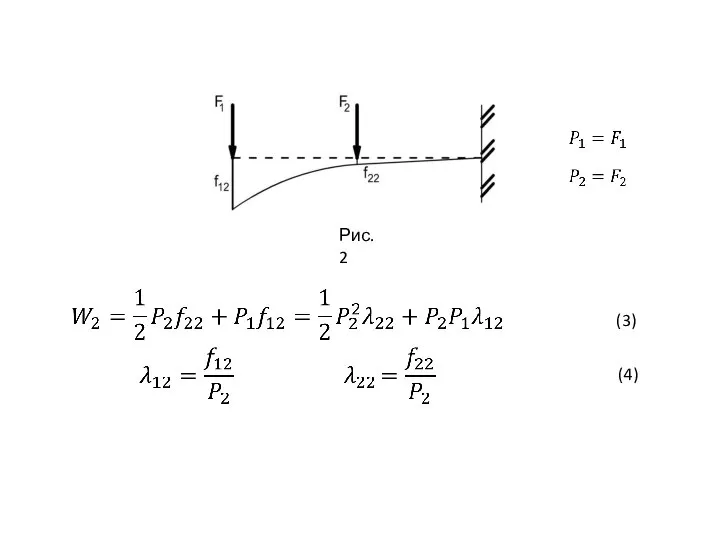
- 10. (3) (4) Рис.2
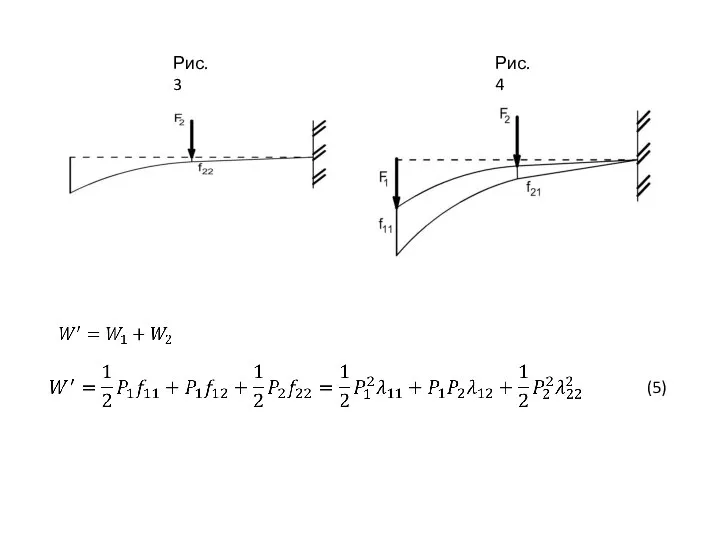
- 11. (5) Рис.3 Рис.4
- 12. (8) (9) (10) (11) (7) (6)
- 13. (12) Теорема Клайперона (13) Потенциальная энергия линейной упруго-деформируемой системы равна половине суммы произведений обобщенных сил на
- 14. (1) (2) (3) (4) (5) y (6) Пример Р характеризует систему взаимно уравновешенных сил: (7) 4.Обобщенные
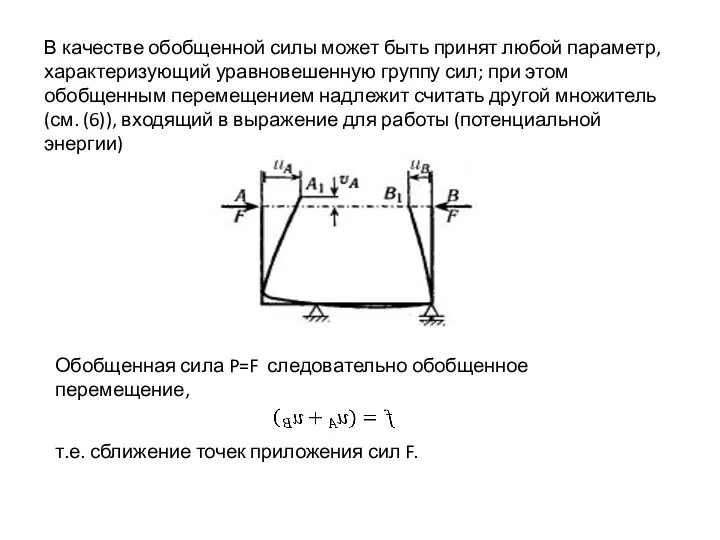
- 15. В качестве обобщенной силы может быть принят любой параметр, характеризующий уравновешенную группу сил; при этом обобщенным
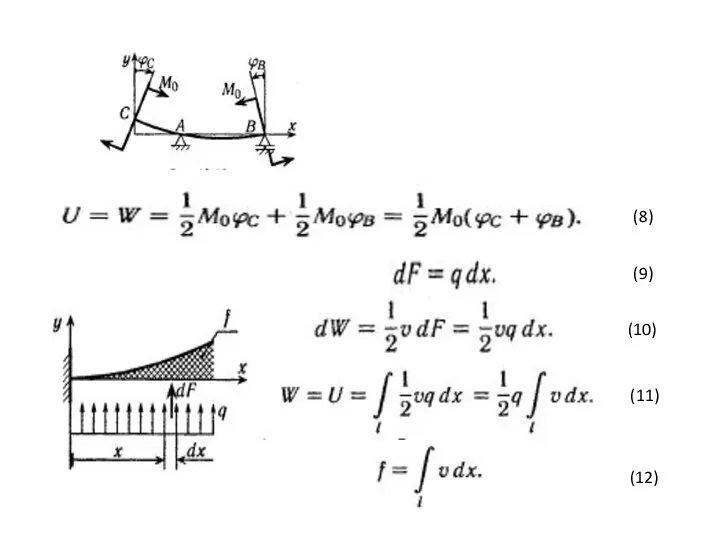
- 16. (8) (9) (10) (11) (12)
- 17. Если (1) (2) (3) (4) (5) (6) 5.ТЕОРЕМА ЛАГРАНЖА
- 18. (7) (8) (9) Теорема Л. Лагранжа: Обобщенная сила равна частной производной от потенциальной энергии упругой деформации
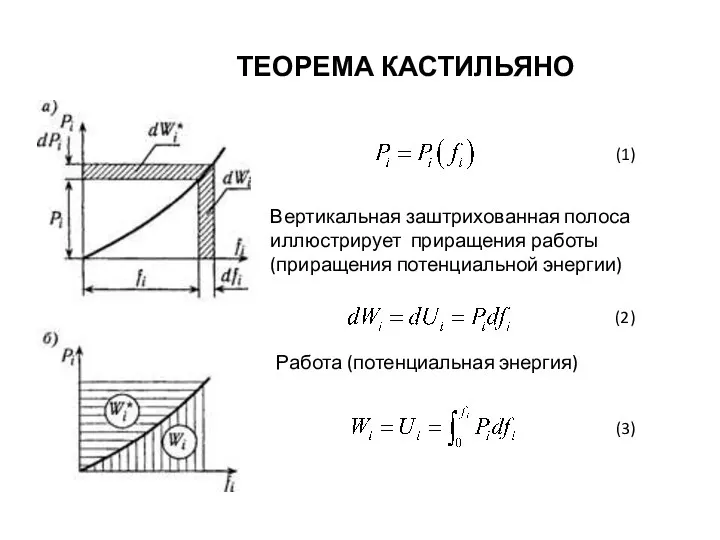
- 19. ТЕОРЕМА КАСТИЛЬЯНО . Вертикальная заштрихованная полоса иллюстрирует приращения работы (приращения потенциальной энергии) Работа (потенциальная энергия) (1)
- 20. Вводится понятие приращения дополнительной работы (дополнительной энергии) горизонтальная заштрихованная полоса ( рис. а.) - дополнительная работа
- 21. Если на упругую систему действуют n сил, то полный дифференциал дополнительной потенциальной энергии принимает вид (4),
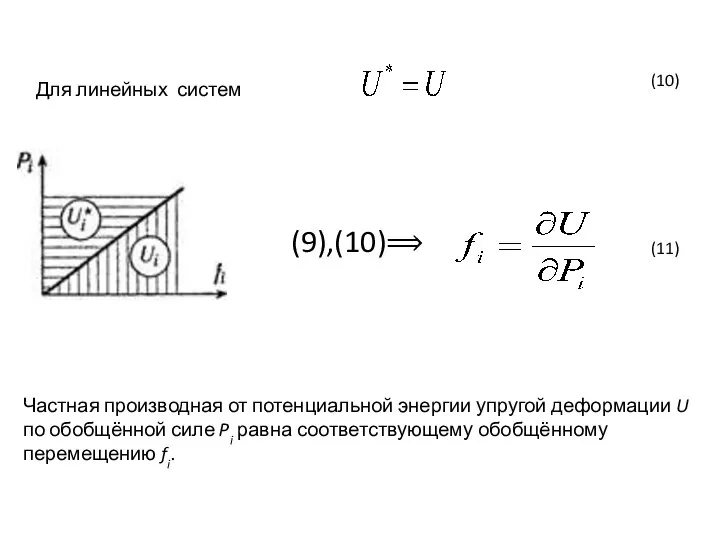
- 22. Для линейных систем . Частная производная от потенциальной энергии упругой деформации U по обобщённой силе Pi
- 23. В случае плоского изгиба Величины Pi и x взаимно независимы, операции дифференцирования и интегрирования можно поменять
- 24. Дифференцирование сложной функции Для изгиба с кручением, растяжением-сжатием и сдвигом по аналогии (15) (16) (17)
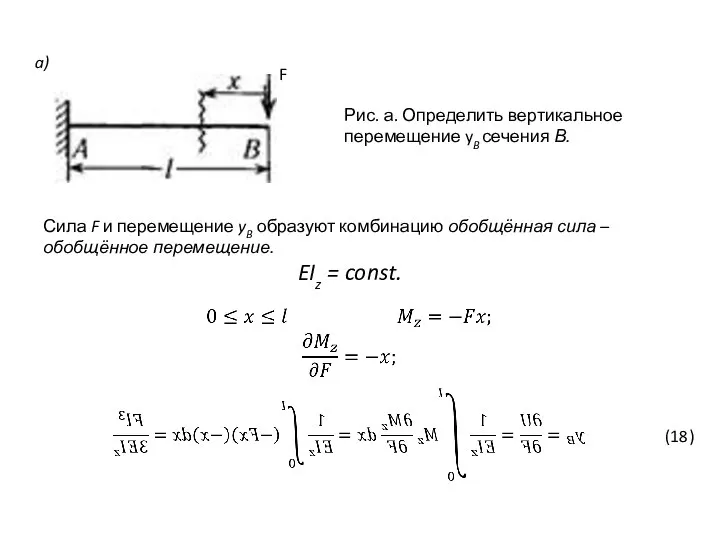
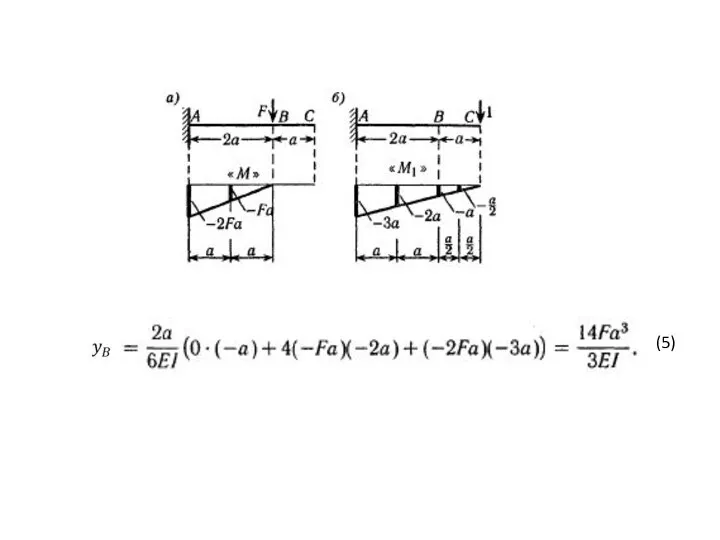
- 25. a) Рис. а. Определить вертикальное перемещение yB сечения В. Сила F и перемещение yB образуют комбинацию
- 26. a a
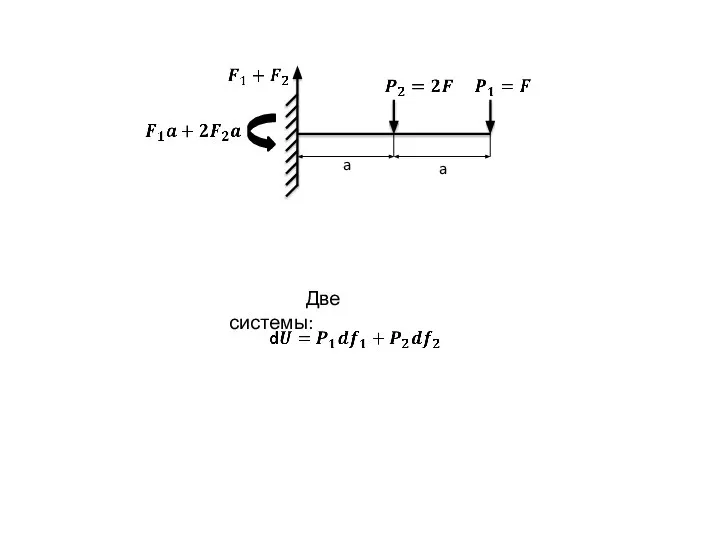
- 27. a a Две системы:
- 28. ++ _
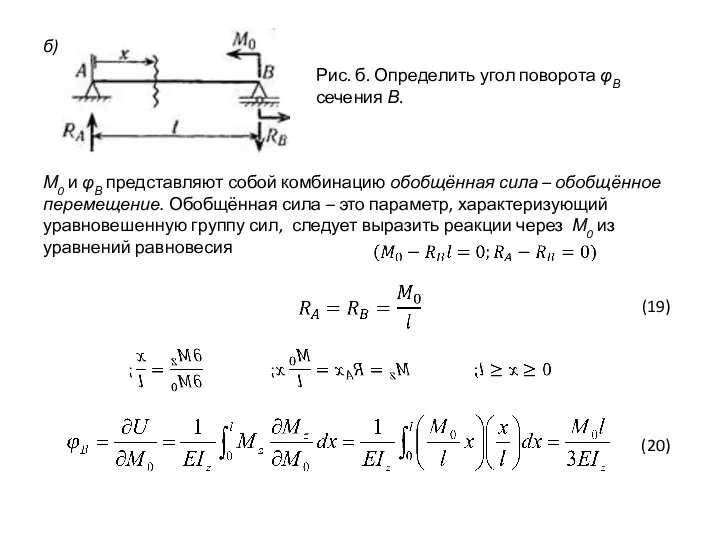
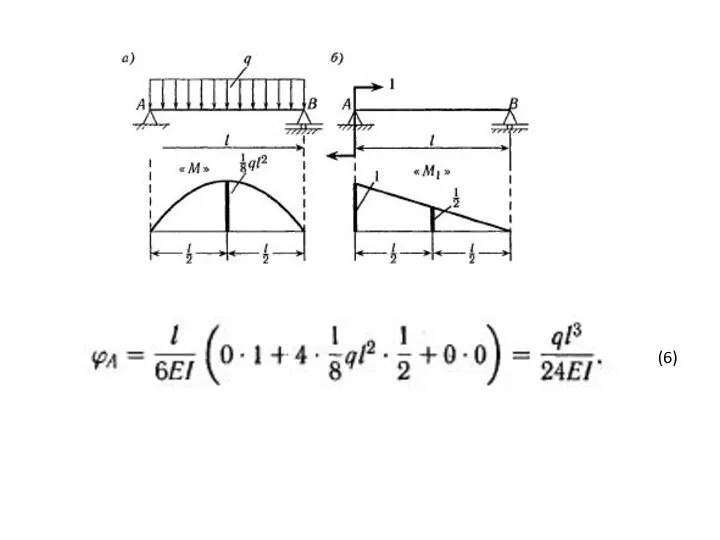
- 29. б) Рис. б. Определить угол поворота φВ сечения В. М0 и φВ представляют собой комбинацию обобщённая
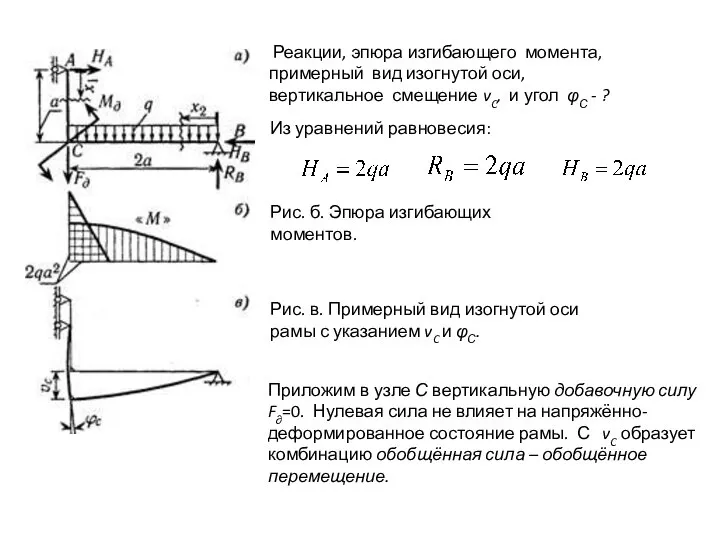
- 30. Реакции, эпюра изгибающего момента, примерный вид изогнутой оси, вертикальное смещение vC, и угол φС - ?
- 31. По теореме Кастильяно: Приложим в узле С добавочный момент М∂ = 0. Он образует с углом
- 32. По теореме Кастильяно: (24) (25) (26)
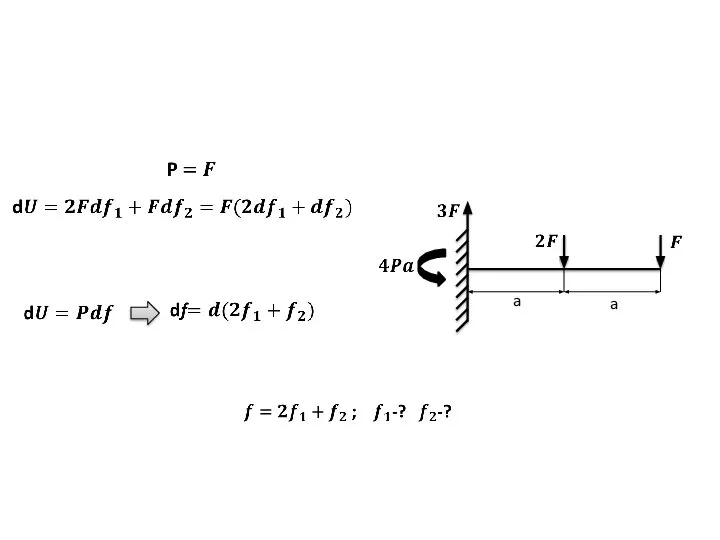
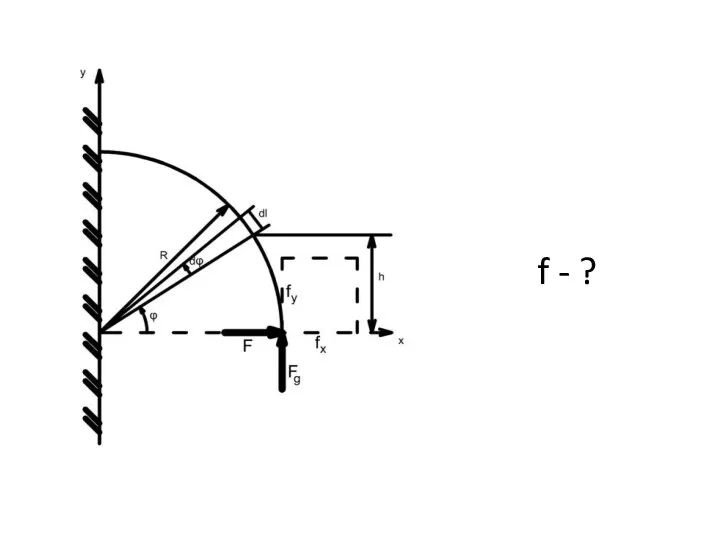
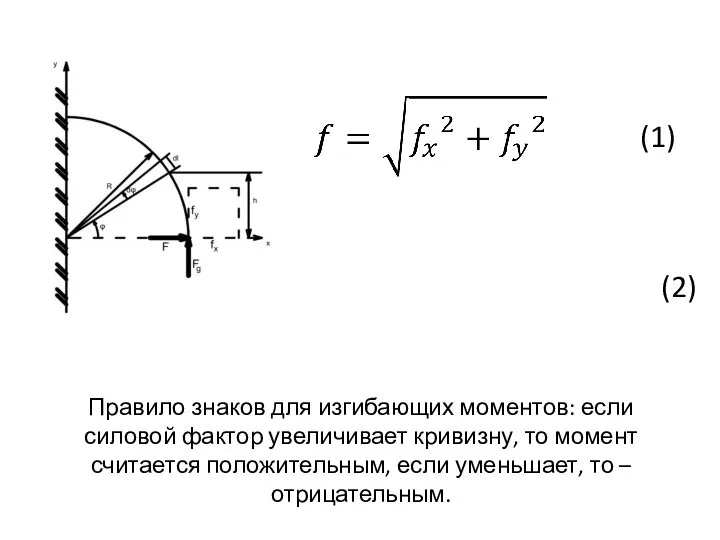
- 33. f - ?
- 34. (1) (2) Правило знаков для изгибающих моментов: если силовой фактор увеличивает кривизну, то момент считается положительным,
- 35. (3) Для вычисления вертикальных перемещений приложим добавочную силу Fg , соответствующую fy . (4) (5)
- 36. (8) (9) (6) (7)
- 37. Эквивалентно (1) 7.Формула Максвелла-Мора (15')
- 38. (2) Дж. Максвелл и О. Мор (3) (4)
- 39. 3 (4) (3) (4) (3) (3)
- 41. (5)
- 42. (6)
- 43. СПАСИБО ЗА ВНИМАНИЕ!
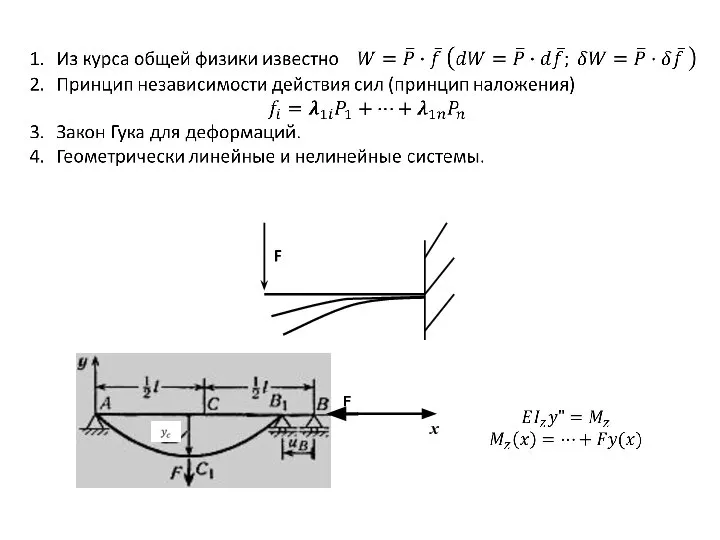
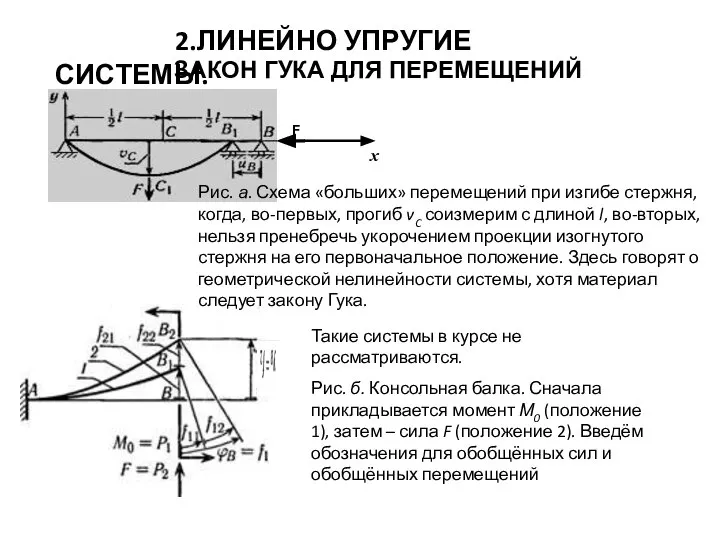
- 45. 2.ЛИНЕЙНО УПРУГИЕ СИСТЕМЫ. ЗАКОН ГУКА ДЛЯ ПЕРЕМЕЩЕНИЙ F Рис. а. Схема «больших» перемещений при изгибе стержня,
- 47. Скачать презентацию

















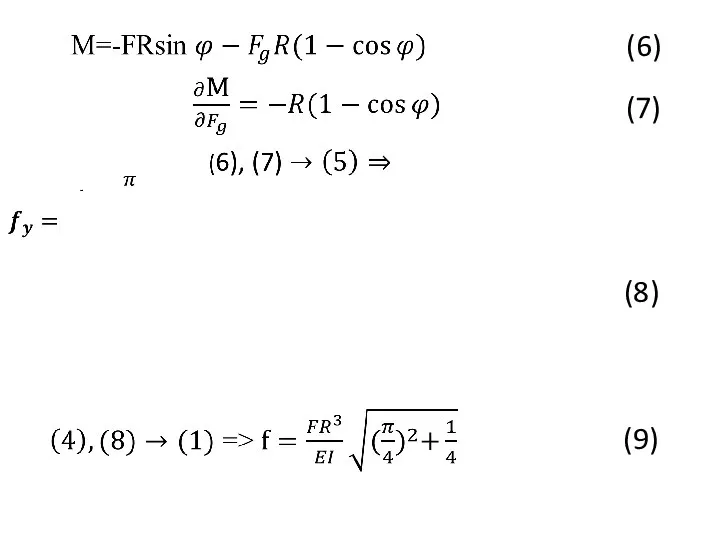





 Процессы теплопередачи. Сложный теплообмен и теплопередача
Процессы теплопередачи. Сложный теплообмен и теплопередача Презентация на тему Производство и использование электрической энергии
Презентация на тему Производство и использование электрической энергии  Момент сил
Момент сил Пьер Кюри (1859-1906) и Мария Склодовская-Кюри (1867-1934)
Пьер Кюри (1859-1906) и Мария Склодовская-Кюри (1867-1934) Презентация на тему Статика и равновесие
Презентация на тему Статика и равновесие  Двухтактный ДВС
Двухтактный ДВС Электроемкость. Конденсаторы
Электроемкость. Конденсаторы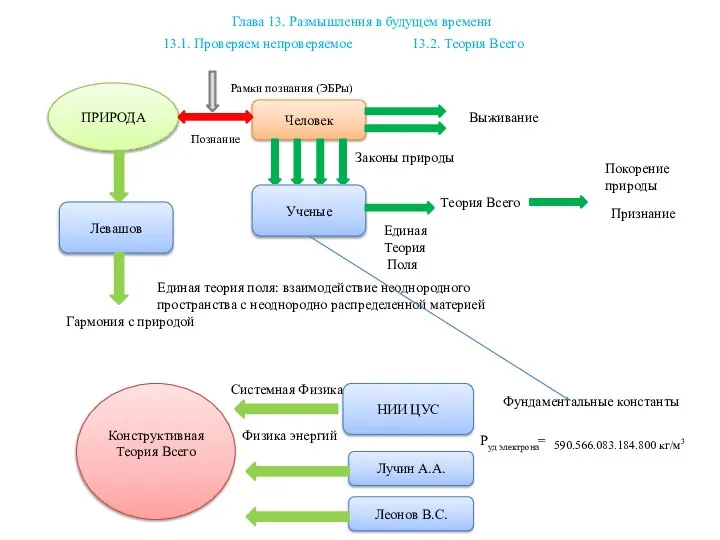 Размышления в будущем времени
Размышления в будущем времени Сельскохозяйственные машины
Сельскохозяйственные машины Презентация на тему Ультразвук и инфразвук
Презентация на тему Ультразвук и инфразвук  Решение задач по теме Закон Кулона
Решение задач по теме Закон Кулона Источники звука. Звуковая энергия. Плотность звуковой энергии. Лекция 4
Источники звука. Звуковая энергия. Плотность звуковой энергии. Лекция 4 Виды тепловых двигателей
Виды тепловых двигателей Уравнения равновесия
Уравнения равновесия Постоянный ток ЭДС и внутреннее сопротивление источника тока. 10 класс
Постоянный ток ЭДС и внутреннее сопротивление источника тока. 10 класс Предмет Теплоносители и их свойства. Параметры состояния. Уравнения состояния газов
Предмет Теплоносители и их свойства. Параметры состояния. Уравнения состояния газов Проверочные работы по физике для 7 – 8 класса
Проверочные работы по физике для 7 – 8 класса Основы динамики
Основы динамики Идеальный газ в МКТ
Идеальный газ в МКТ Презентация на тему Силы всемирного тяготения
Презентация на тему Силы всемирного тяготения  Решение задач Закон сохранения энергии
Решение задач Закон сохранения энергии Явление электромагнитной индукции
Явление электромагнитной индукции Автор: Тараканова Светлана школа № 14, 8 А класс
Автор: Тараканова Светлана школа № 14, 8 А класс Молекулярно-кинетическая теория идеальных газов
Молекулярно-кинетическая теория идеальных газов Магнитное поле. Лекция 20
Магнитное поле. Лекция 20 Способ уменьшения ударов в шагающем механизме
Способ уменьшения ударов в шагающем механизме Динамические звенья и преобразование структурных схем
Динамические звенья и преобразование структурных схем Исследовать зависимость дальности полёта снаряда от угла вылета
Исследовать зависимость дальности полёта снаряда от угла вылета