Содержание
- 2. Корпускулярно-волновой дуализм Гипотеза Луи де Бройля о волновых свойствах микрочастиц Корпускулярно-волновой дуализм электромагнитного излучения Дифракция микрочастиц
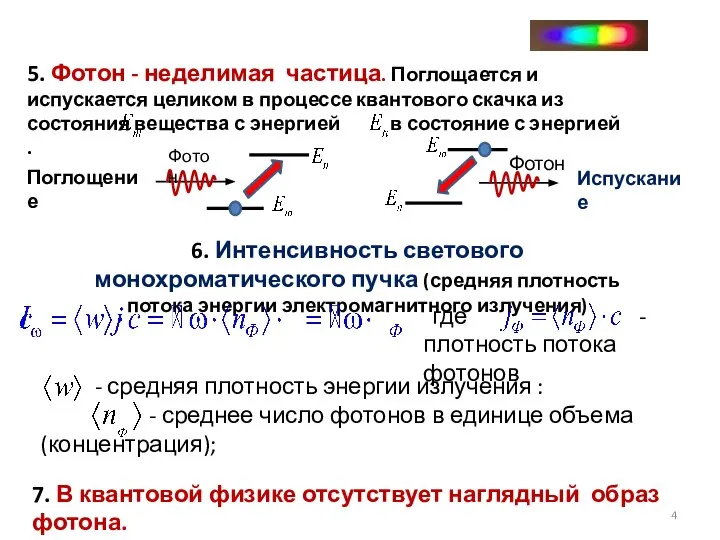
- 3. Ф о т о н Свет и любое электромагнитное излучение – поток фотонов. Корпускулярные свойства излучения.
- 4. 7. В квантовой физике отсутствует наглядный образ фотона.
- 5. Корпускулярно – волновой дуализм электромагнитного излучения Такие явления, как интерференция, дифракция, поляризация света, были объяснены, исходя
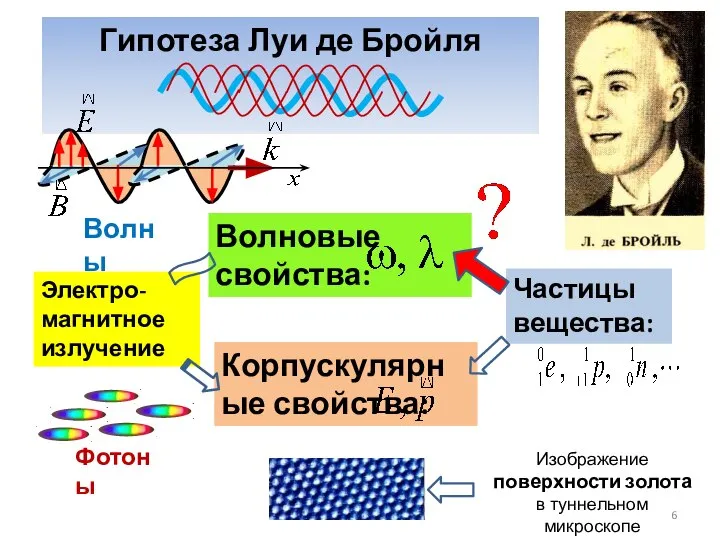
- 6. Изображение поверхности золота в туннельном микроскопе Волны
- 7. Гипотеза де Бройля В 1923 г. Французский физик Луи де Бройль выдвинул чрезвычайно смелую гипотезу: Электромагнитное
- 8. Свободной частице с энергией E и импульсом p, движущейся вдоль оси x, соответствует плоская волна де
- 9. Групповая скорость волны де Бройля Групповая скорость световой волны: Групповая скорость волны де Бройля: Дифференцируя формулу
- 10. . Волна де Бройля не является волной, движущейся вместе с частицей. Волна де Бройля и частица
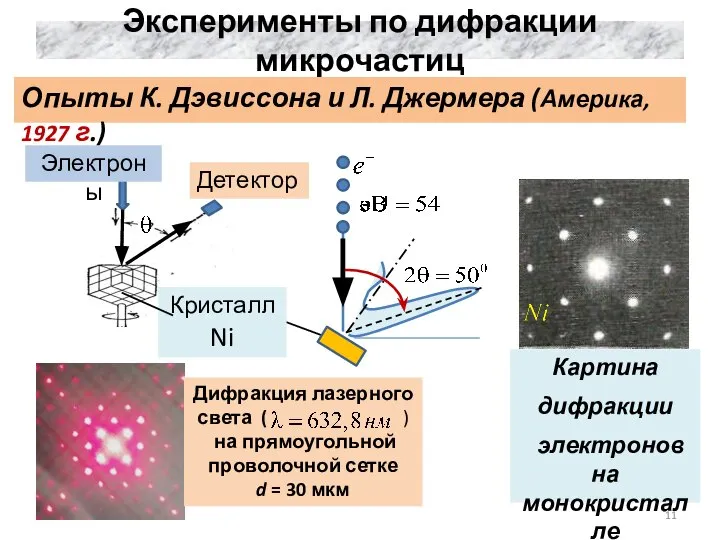
- 11. Эксперименты по дифракции микрочастиц Опыты К. Дэвиссона и Л. Джермера (Америка, 1927 г.)
- 12. Отражение электронов от атомных плоскостей в кристалле. Атомная структура кристаллов была известна из опытов по дифракции
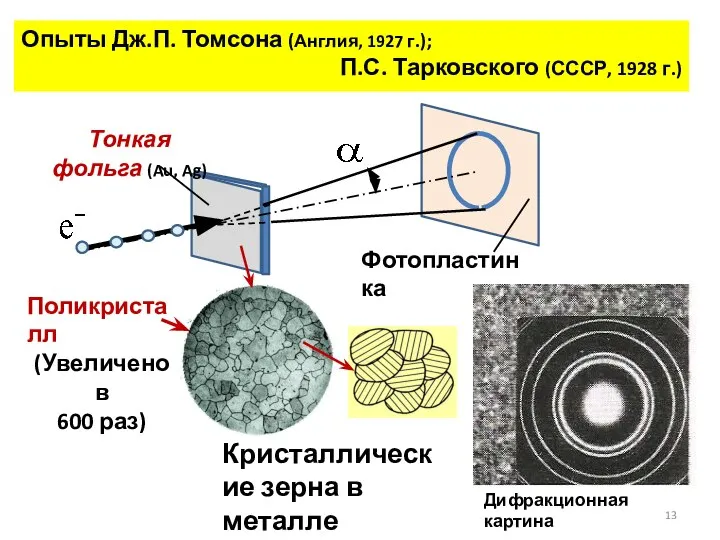
- 13. Опыты Дж.П. Томсона (Англия, 1927 г.); П.С. Тарковского (СССР, 1928 г.) Кристаллические зерна в металле Поликристалл
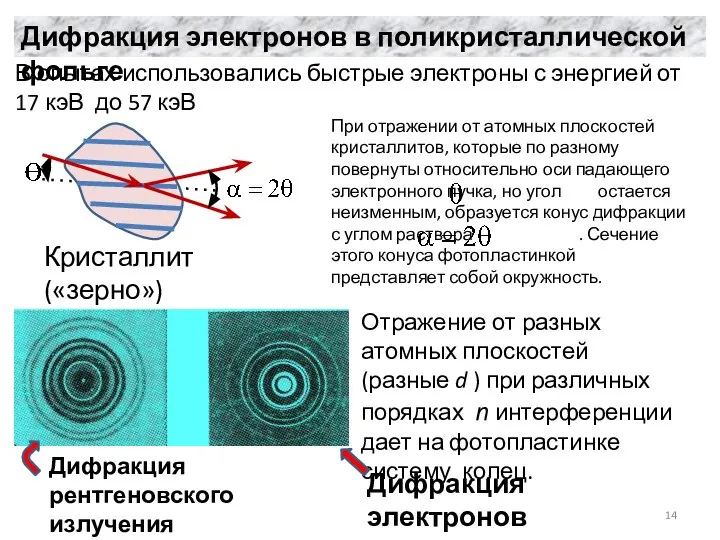
- 14. Дифракция электронов в поликристаллической фольге В опытах использовались быстрые электроны с энергией от 17 кэВ до
- 15. Дифракция одиночных электронов Дифракция одиночных электронов Группа физиков во главе с В.А.Фабрикантом в СССР выполнила в
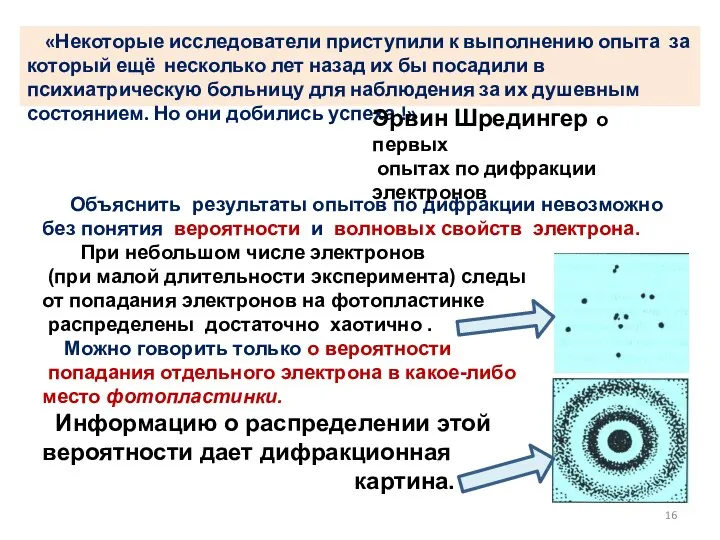
- 16. «Некоторые исследователи приступили к выполнению опыта за который ещё несколько лет назад их бы посадили в
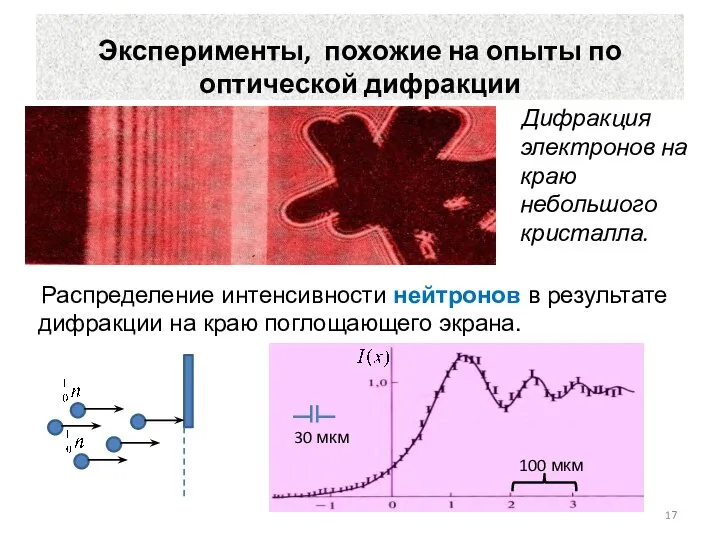
- 17. Эксперименты, похожие на опыты по оптической дифракции Распределение интенсивности нейтронов в результате дифракции на краю поглощающего
- 18. О новой механике движения микрочастиц – квантовой механике На заре квантовой механики (1920-е годы) физики пытаются
- 19. Еще до начала экспериментов по дифракции электронов физики-теоретики Вернер Гейзенберг в Германии и Эрвин Шредингер в
- 20. Принцип дополнительности Н. Бора. Соотношения неопределенностей 1927г. Нильс Бор в Дании сформулировал принцип дополнительности в квантовых
- 21. Соотношения неопределенностей. Примеры мысленных экспериментов.
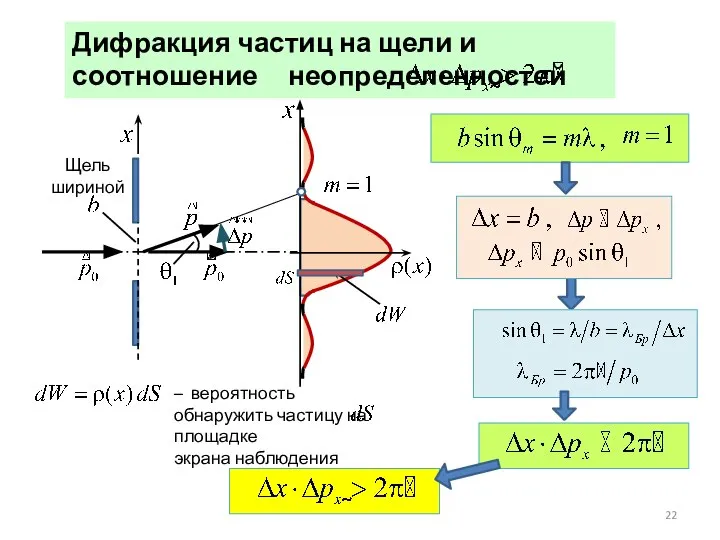
- 23. Соотношения неопределенностей – частный случай и конкретное выражение принципа дополнительности Н. Бора. Соотношения неопределенностей В. Гейзенберга
- 24. Следствия из соотношений неопределенностей Н.Бор часто вспоминал, как в 50-х годах к нему после лекции подошел
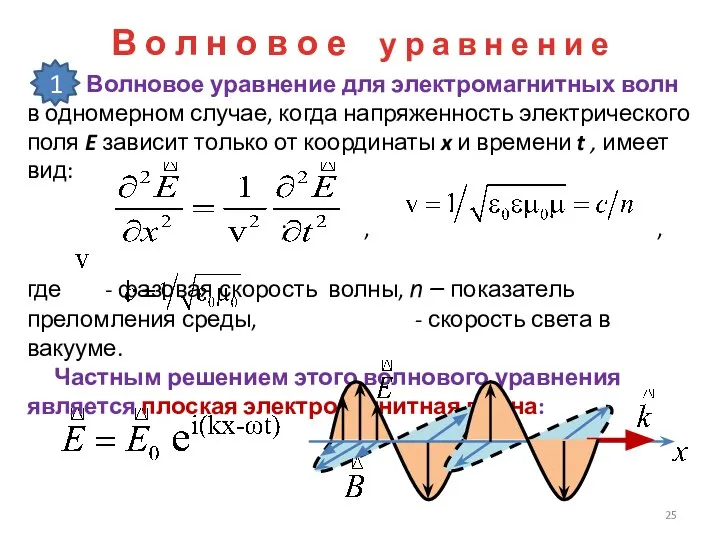
- 25. В о л н о в о е у р а в н е н и
- 26. Волновое уравнение Шредингера В 1926 г. австрийский физик-теоретик Эрвин Шредингер разработал теорию движения микрочастиц, в основу
- 27. Вероятностный смысл
- 28. В классической физике статистические методы, использующие понятие вероятности, рассматриваются как вспомогательные, и применяются в тех случаях,
- 29. В квантовой физике, согласно М.Борну, ситуация совсем иная. Электронам, протонам, фотонам и другим частицам присущи волновые
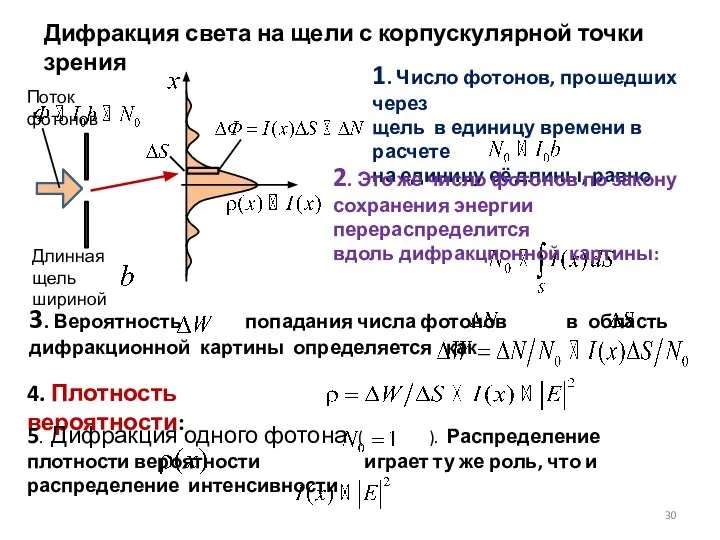
- 30. Дифракция света на щели с корпускулярной точки зрения
- 31. О вероятности обнаружения электрона, который свободно движется в направлении оси x
- 32. Уравнение Шредингера в символическом представлении Макс Борн в том же 1926 году высказал идею , суть
- 33. 2. Уравнение Шредингера где потенциальная энергия – функция координат, ей соответствует оператор умножения: .
- 35. Скачать презентацию






















 Общий порядок построения эпюр Qx и Мх
Общий порядок построения эпюр Qx и Мх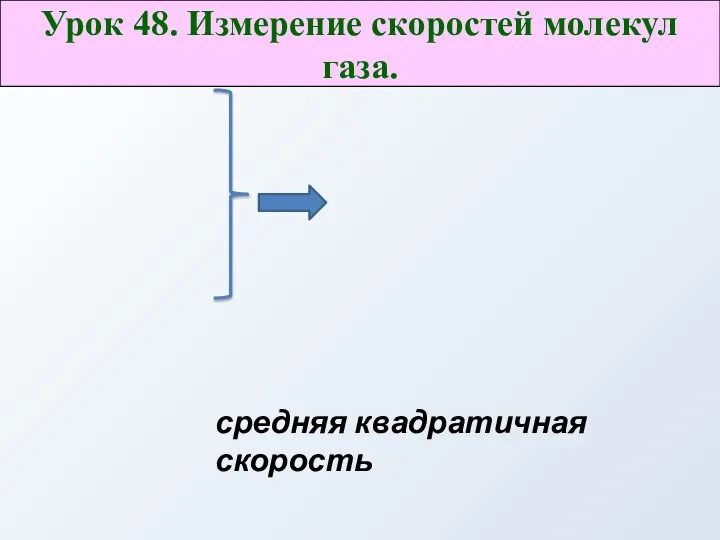 Измерение скоростей молекул газа. (Урок 48)
Измерение скоростей молекул газа. (Урок 48) Механика. Молекулярная физика
Механика. Молекулярная физика Неисправность источники электрической энергии, способы проверки и ремонта
Неисправность источники электрической энергии, способы проверки и ремонта Виды энергии
Виды энергии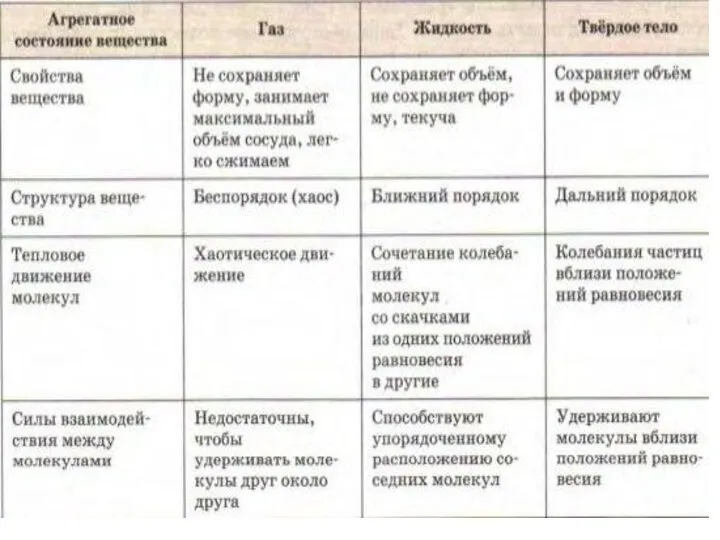 Свойства жидкостей
Свойства жидкостей Трение. Сила трения. Коэффициент трения скольжения
Трение. Сила трения. Коэффициент трения скольжения Тепловые двигатели
Тепловые двигатели Дифракция света
Дифракция света Волновые свойства света
Волновые свойства света Закон сохранения момента импульса
Закон сохранения момента импульса Теплотехнические измерения. Практическое занятие
Теплотехнические измерения. Практическое занятие Электропривод. Проектирование электроприводов
Электропривод. Проектирование электроприводов Оптика. Законы отражения
Оптика. Законы отражения Интерференция света
Интерференция света Физико-химические методы анализа
Физико-химические методы анализа Презентация на тему Перспективы развития физики
Презентация на тему Перспективы развития физики  Скорость движения
Скорость движения Погрузочно-транспортные машины типа пд и пт
Погрузочно-транспортные машины типа пд и пт Шалаев Хиггс
Шалаев Хиггс Задачи. Мощность
Задачи. Мощность Отраслевая олимпиада ПАО РусГидро по физике Энергия образования для школьников 7-11 классов
Отраслевая олимпиада ПАО РусГидро по физике Энергия образования для школьников 7-11 классов Условия плавания тел
Условия плавания тел Презентация на тему Закон Ома для участка цепи
Презентация на тему Закон Ома для участка цепи  Лазерные технологии
Лазерные технологии Гармонические колебания. Амплитуда, период и частота колебательного движения
Гармонические колебания. Амплитуда, период и частота колебательного движения Оптика. Законы преломления
Оптика. Законы преломления Понятие о машине и механизме. Урок Технология
Понятие о машине и механизме. Урок Технология