Содержание
- 2. Сарина Марина Павловна Доцент кафедры Прикладной и теоретической физики, IV -210
- 3. Иродов И.Е. Основные законы механики Трофимова Т.И. Курс физики Cарина.М.П. Механика, молекулярная физика , термодинамика. Часть
- 4. Есть в библиотеке и в электронной библиотечной системе НГТУ (ЭБС)
- 5. Лабораторный практикум
- 9. Курс на dispace № 12724 ФЭН 2022 физика Физика механика № 4420 Физика введение № 7821
- 10. ЭЛЕМЕНТЫ КИНЕМАТИКИ
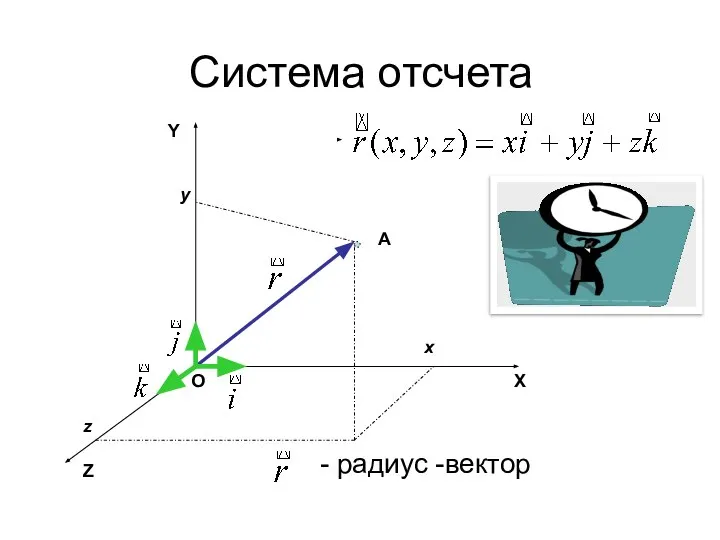
- 11. Система отсчета Y Z X O A x z y - радиус -вектор
- 12. Система отсчета – это система координат, указывающая положение тела в пространстве, + часы, необходимые для отсчета
- 13. Мы будем пользоваться декартовой системой координат
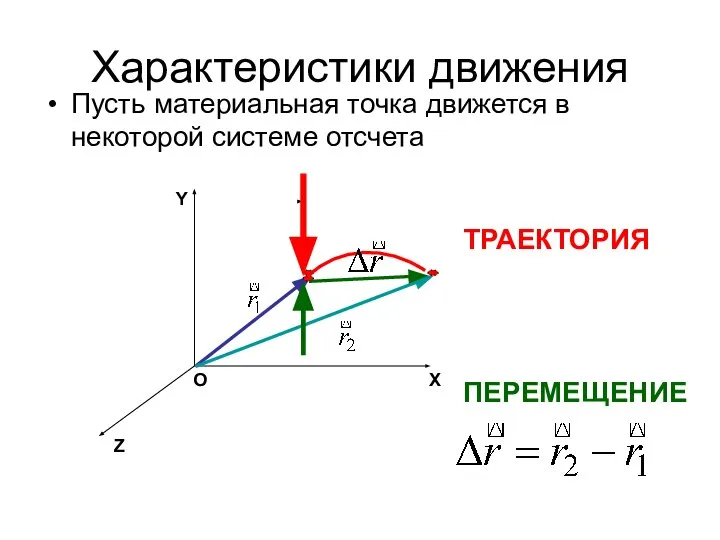
- 14. Характеристики движения Пусть материальная точка движется в некоторой системе отсчета Y Z X O ТРАЕКТОРИЯ ПЕРЕМЕЩЕНИЕ
- 15. Траектория – это линия, вдоль которой материальная точка движется в пространстве Вектор перемещения проводится из начальной
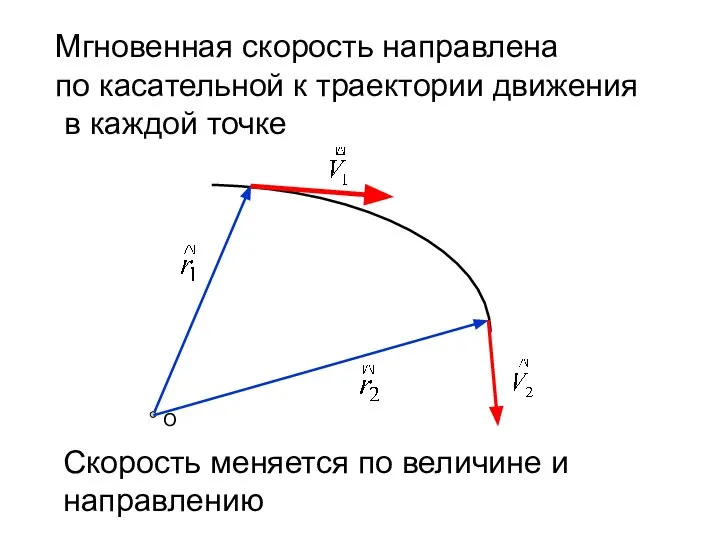
- 16. Мгновенная скорость
- 17. Мгновенная скорость направлена по касательной к траектории движения в каждой точке Скорость меняется по величине и
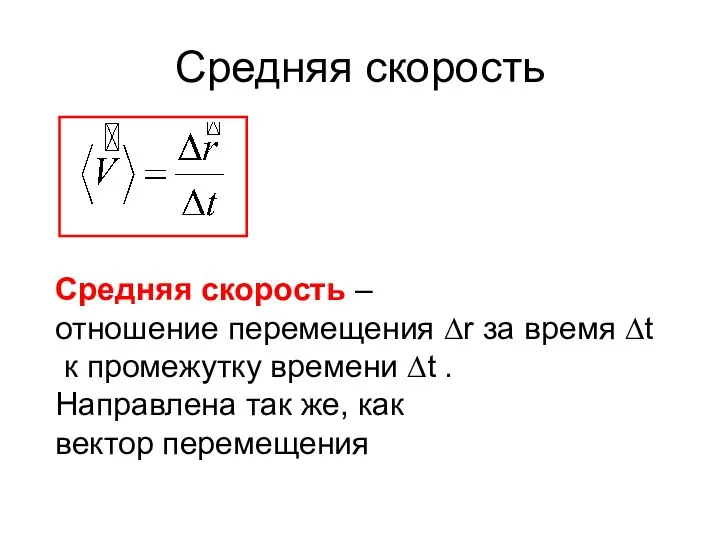
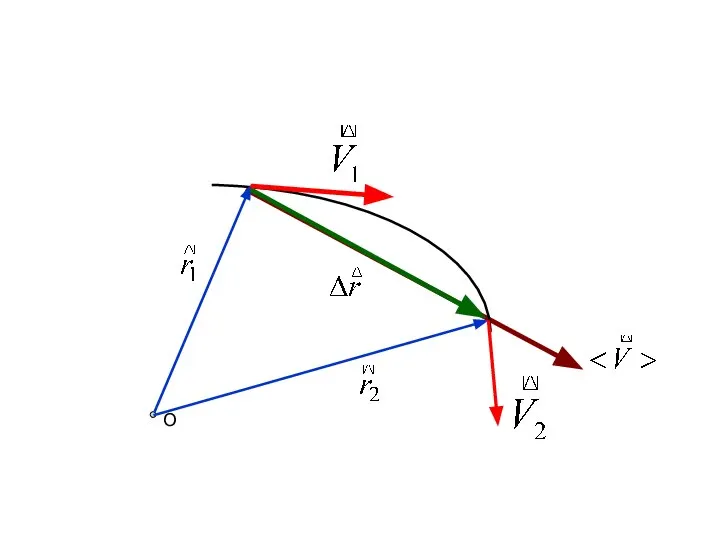
- 18. Средняя скорость Средняя скорость – отношение перемещения ∆r за время ∆t к промежутку времени ∆t .
- 20. Ускорение Ускорение-быстрота изменения скорости по модулю и направлению
- 21. Мгновенное ускорение Мгновенное ускорение – первая производная скорости по времени.
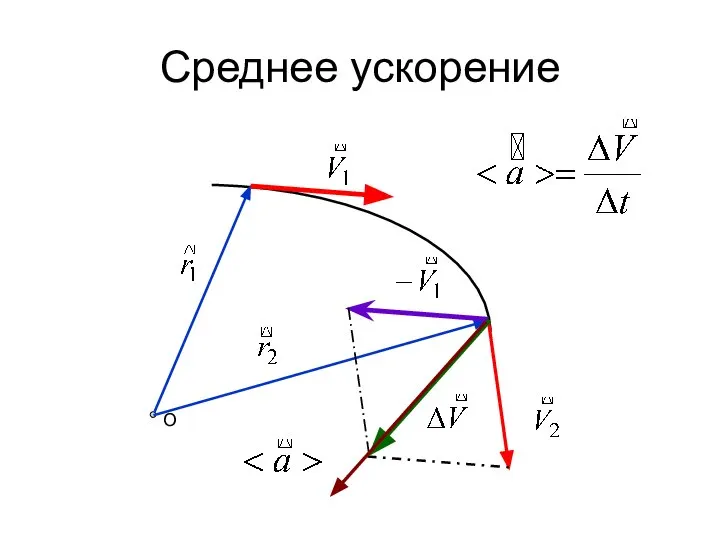
- 22. Среднее ускорение
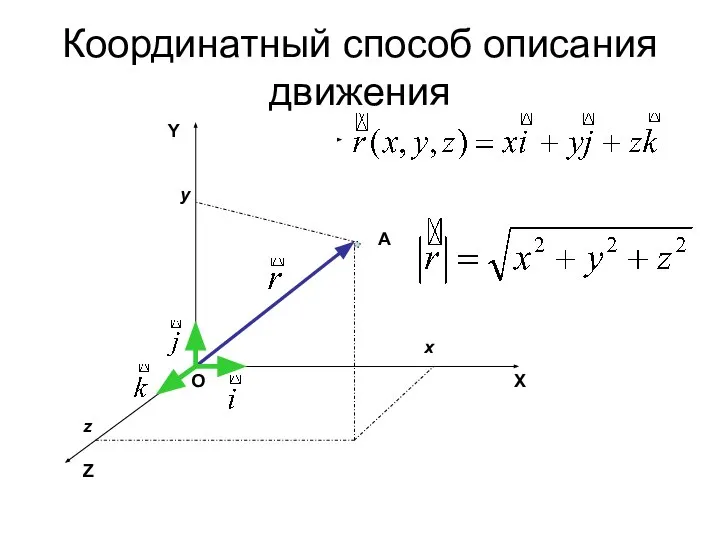
- 23. Координатный способ описания движения Y Z X O A x z y
- 25. аналогично для ускорения
- 26. Криволинейное движение
- 27. В некоторых случаях не удобно раскладывать ускорение на координатные составляющие Естественный метод ( удобно применять, когда
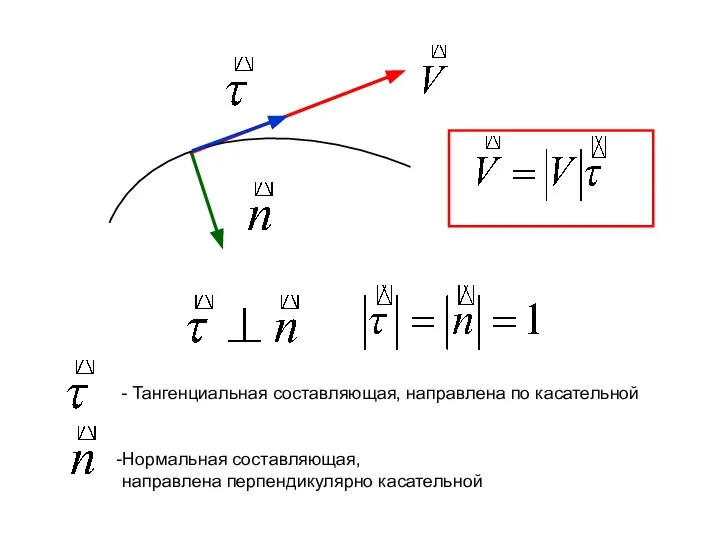
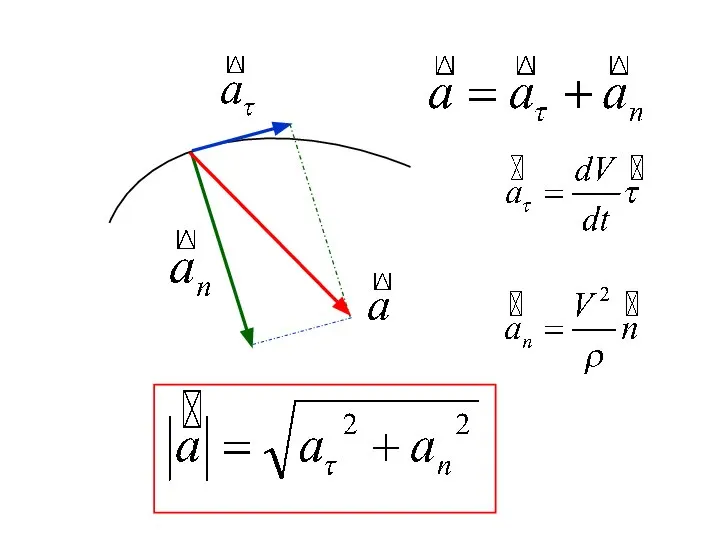
- 28. - Тангенциальная составляющая, направлена по касательной Нормальная составляющая, направлена перпендикулярно касательной
- 29. - Тангенциальное ускорение Определяет быстроту изменения скорости по величине
- 30. Направление вектора ? единичный вектор Скалярное произведение Продифференцируем
- 31. Вектора перпендикулярны направлен по направлению нормали Второе слагаемое в формуле ускорения
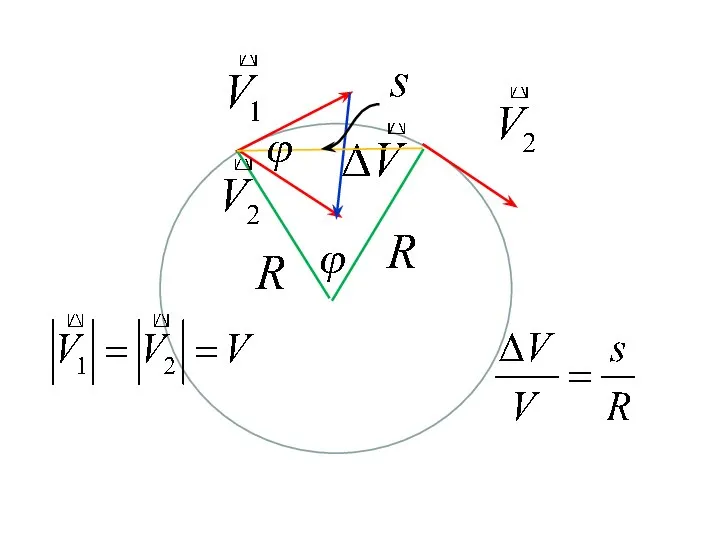
- 33. При малых углах
- 34. - радиус кривизны траектории - Нормальное ускорение Определяет быстроту изменения скорости по направлению
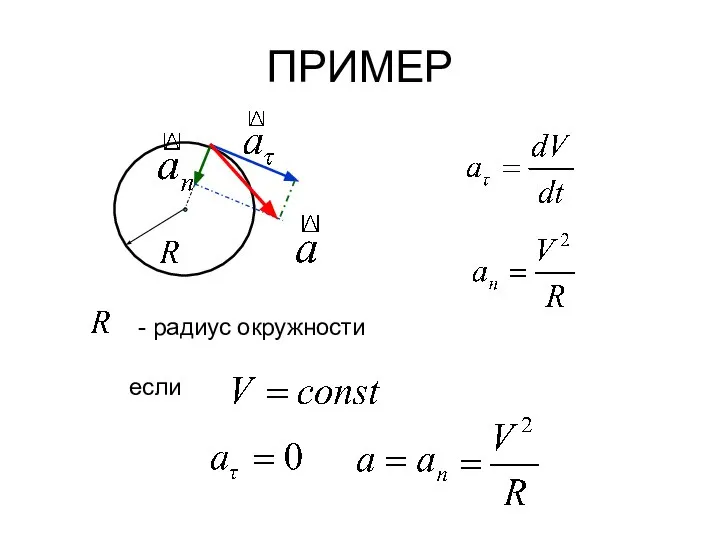
- 36. ПРИМЕР если - радиус окружности
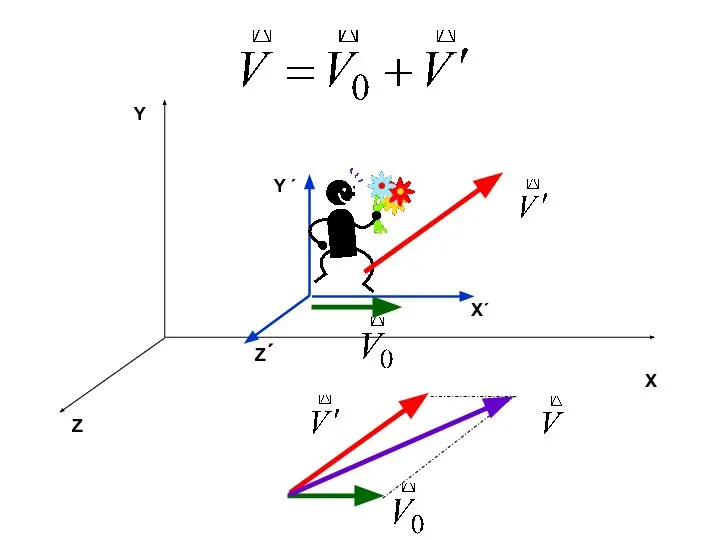
- 37. Закон сложения скоростей
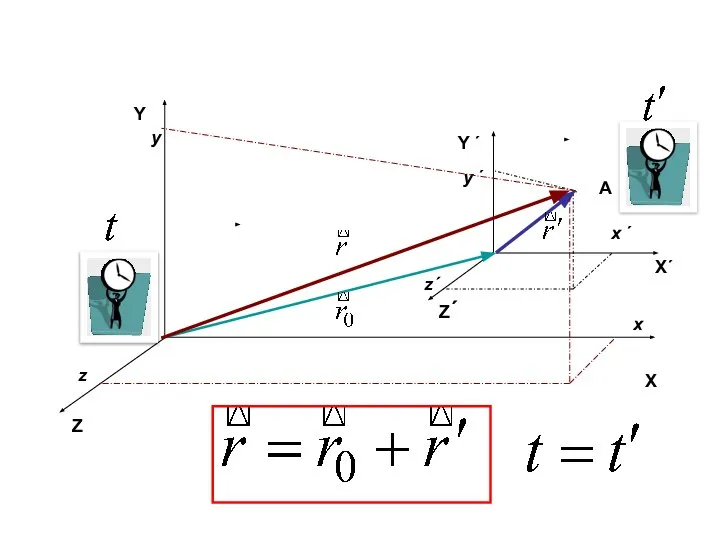
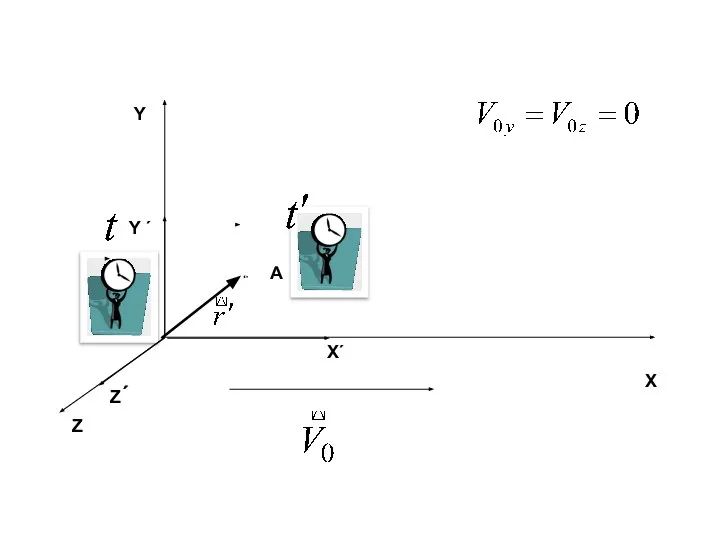
- 38. Y ´ Z´ X´ A x ´ z´ y ´ Y Z X x z y
- 39. Пусть система отсчета К´ движется относительно системы отсчета К со скоростью V0 Системы отсчета движущаяся равномерно
- 41. В проекциях на оси координат V0x, V0y,, V0z – проекции скорости на оси координат
- 42. Закон сложения скоростей
- 43. Скорость движения точки относительно системы отсчета К Скорость движения точки относительно системы отсчета К´ Скорость движения
- 44. Y Z X Y ´ Z´ X´
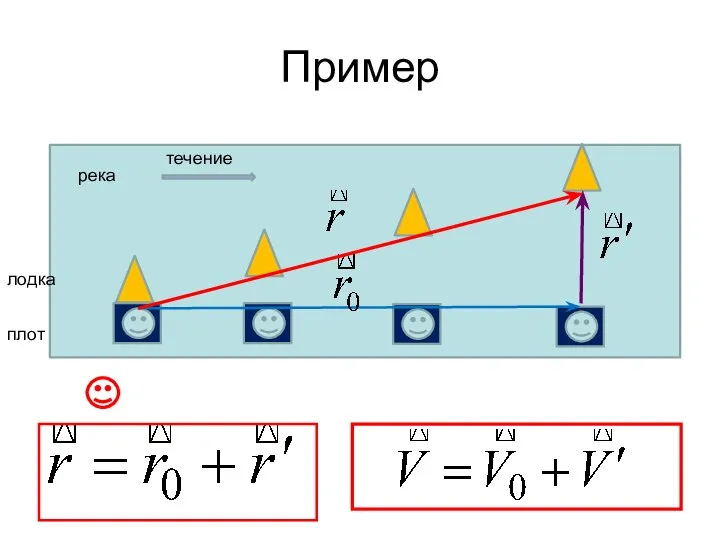
- 45. Пример река плот лодка течение
- 46. ПРЕОБРАЗОВАНИЯ ГАЛИЛЕЯ
- 47. Y Z X
- 50. Принцип относительности Галилея Все законы механики имеют одинаковую форму во всех инерциальных системах отсчета
- 52. Скачать презентацию












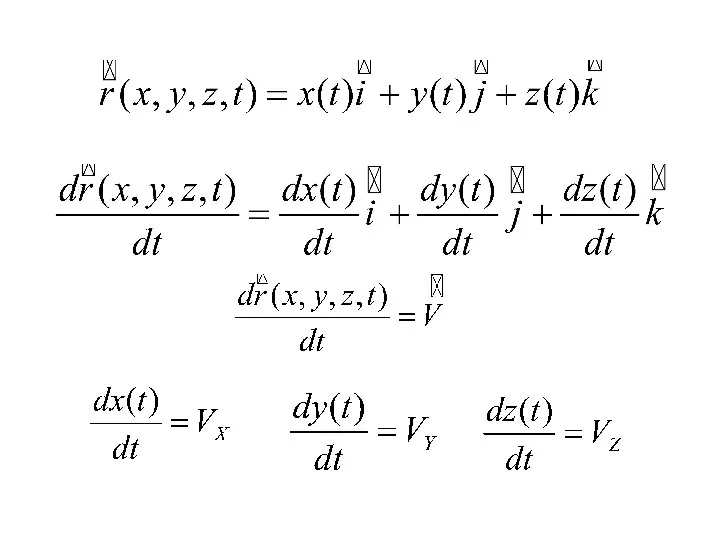






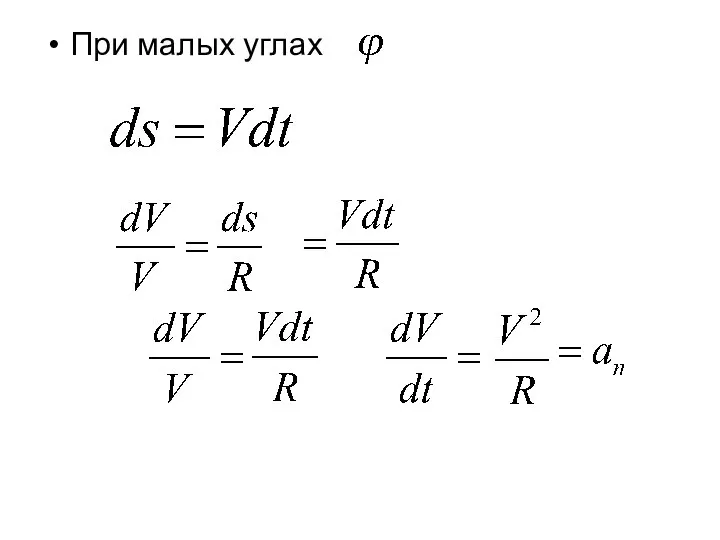



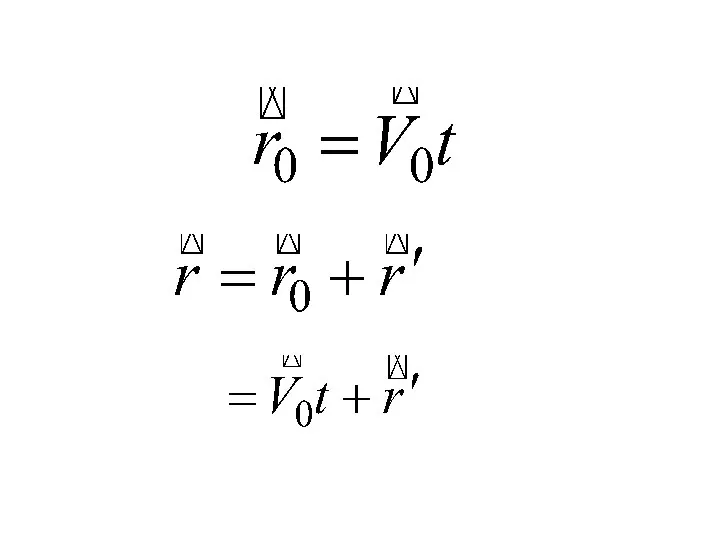




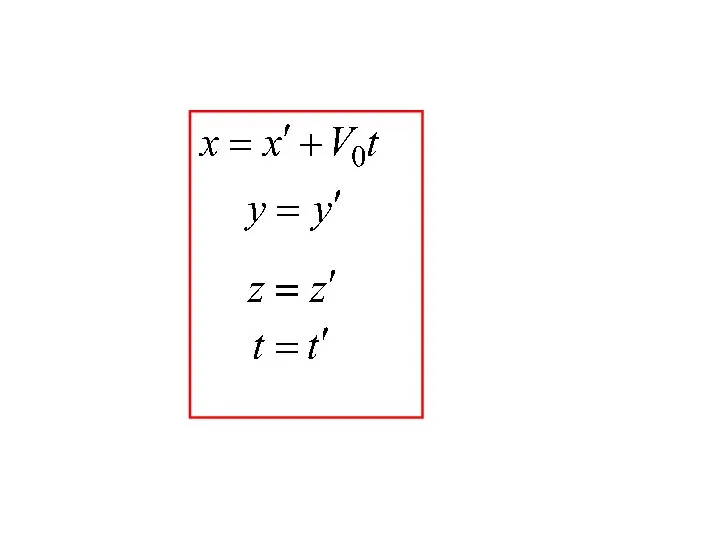
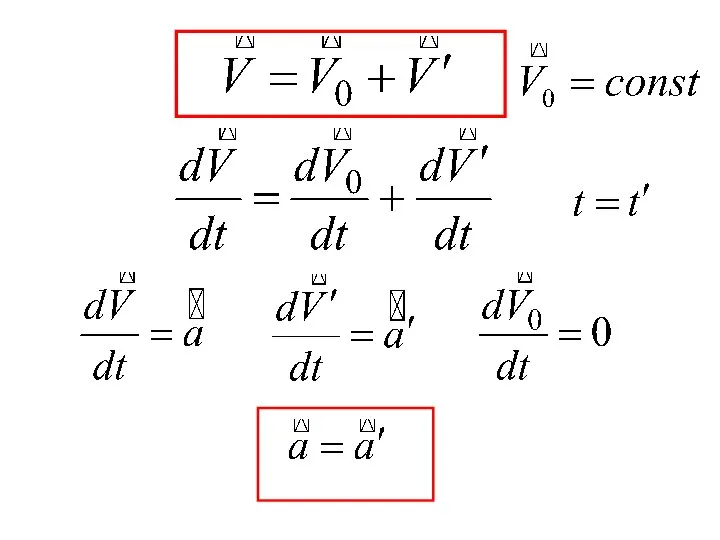

 Излучение
Излучение Физика дайвинга
Физика дайвинга Сложение сил. Равнодействующая сила
Сложение сил. Равнодействующая сила Меры защиты человека при косвенном прикосновении. Устройство защитного отключения (УЗО) на дифференциальном токе
Меры защиты человека при косвенном прикосновении. Устройство защитного отключения (УЗО) на дифференциальном токе Викторина по физике
Викторина по физике Вакуумметры. Характеристики вакуумметров
Вакуумметры. Характеристики вакуумметров Презентация к уроку
Презентация к уроку Статика. Понятия и определения
Статика. Понятия и определения Электрический ток. Источники тока
Электрический ток. Источники тока Обозначение трехвинтовых насосов
Обозначение трехвинтовых насосов Опрделение силы веса, координат центра тяжести и предельных значений статических углов против опрокидывания трактора
Опрделение силы веса, координат центра тяжести и предельных значений статических углов против опрокидывания трактора Электроснабжение и основы электротехники. Цепи постоянного тока. Лекции 1 и 2
Электроснабжение и основы электротехники. Цепи постоянного тока. Лекции 1 и 2 Кинематика. Средняя скорость
Кинематика. Средняя скорость Естественная радиоактивность. Закон радиоактивного распада
Естественная радиоактивность. Закон радиоактивного распада Механические колебания
Механические колебания Презентация на тему Основные акустические опасные факторы воздействия на человека
Презентация на тему Основные акустические опасные факторы воздействия на человека  Паровая машина Ползунова
Паровая машина Ползунова Механическое движение. 6 класс
Механическое движение. 6 класс Энергия. Законы сохранения в механике
Энергия. Законы сохранения в механике Задачи на энергию
Задачи на энергию Радиационный контроль дефектоскопов
Радиационный контроль дефектоскопов Численные методы и оптимизация траекторий межпланетных траекторий
Численные методы и оптимизация траекторий межпланетных траекторий Коробки передач. Рабочие процессы
Коробки передач. Рабочие процессы Dīzeļlokomotīvju bremžu iekārtu shēmas
Dīzeļlokomotīvju bremžu iekārtu shēmas Презентация на тему Кипение
Презентация на тему Кипение  Управляемость. Тема 6
Управляемость. Тема 6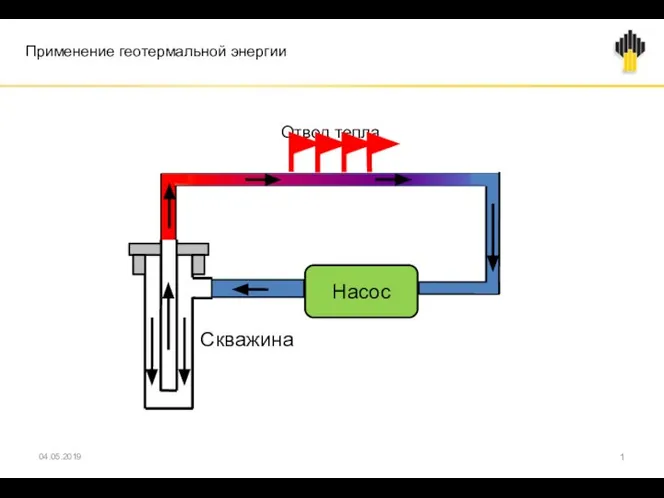 Применение геотермальной энергии
Применение геотермальной энергии Тепловые двигатели
Тепловые двигатели