Физика Лекция 2

ЦИРКУЛЯЦИЯ ВЕКТОРА НАПРЯЖЕННОСТИ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ

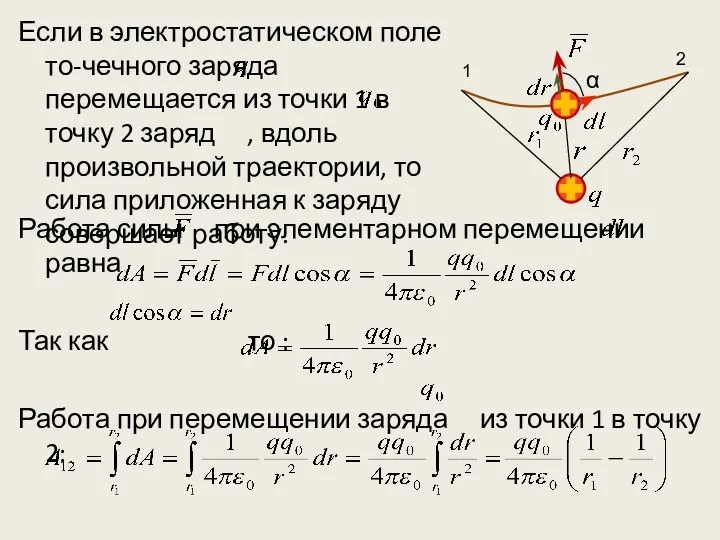
Если в электростатическом поле то-чечного заряда перемещается из точки 1 в точку 2 заряд , вдоль произвольной траектории, то сила приложенная к заряду совершает работу.
Работа силы при элементарном перемещении равна
Так как то :
Работа при перемещении заряда из точки 1 в точку 2:

Работа А не зависит от траектории перемещения, а оп-ределяется только положениями начальной и конеч-ной точек. Значит электростатическое поле точечного заряда является потенциальным, а электростатичес-кие силы – консервативными.
Работа А совершаемая при перемещении электрическо-го заряда во внешнем электростатическом поле по любому замкнутому пути L равна нулю.
Если в качестве заряда переносимого в электростати-ческое поле взять единичный точечный заряд, то эле-ментарная работа сил поля на пути равна
Где - проекция вектора на направление элементарного перемещения.

Интеграл - циркуляция вектора напряжен-ности.
Циркуляция вектора напряженности электростатическо-го поля вдоль любого замкнутого контура равна нулю. Силовое поле, обладающее этим свойством называет-ся потенциальным.
Из обращения в 0 циркуляции вектора , следует, что линии напряженности электростатического поля НЕ МОГУТ БЫТЬ ЗАМКНУТЫМИ. Они начинаются и закан-чиваются на положительных и отрицательных зарядах соответственно, или уходят в бесконечность.
Эта формула справедлива только для электростатическо-го поля, для поля движущихся зарядов, условие не выполняется.

ПОТЕНЦИАЛ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ

Тело находящееся в потенциальном поле сил, обладает потенциальной энергией, за счет которой силами поля совершается работа. Работа консервативных сил поля совершается за счет убыли потенциальной энергии. Поэтому работу сил электростатического поля можно представить как разность потенциальных энергий, ко-торыми обладает точечный заряд в начальной и ко-нечной точках поля заряда .
Отсюда получается, что потенциальная энергия заряда
При удалении заряда в бесконечность ( ), потенци-альная энергия превращается в нуль ( ), значит

, и потенциальная энергия заряда находящего-ся в электростатическом поле, создаваемом зарядом на расстоянии от него будет равна:
Для одноименных зарядов произведение и потен-циальная энергия их взаимодействия положительна (отталкивание), для разноименных зарядов и потенциальная энергия их взаимодействия отрица-тельна (притяжение).
Если поле создается системой точечных зарядов , то, работа электростатических сил, совершаемая над зарядом равна алгебраической сумме работ сил об-условленных каждым зарядом по отдельности.

Потенциальная энергия заряда находящегося в этом поле, равна сумме его потенциальных энергий соз-даваемых каждым из зарядов в отдельности.
Отношение не зависит от и является энергети-ческой характеристикой электростатического поля и называется ПОТЕНЦИАЛ – ϕ.
Потенциал в какой либо точке электростатического поля это физическая величина определяемая потенциаль-ной энергией единичного положительного заряда по-мещаемого в данную точку.

Потенциал поля создаваемого точечным зарядом равен
Если поле создается несколькими зарядами, то потен-циал поля системы зарядов равен алгебраической сумме потенциалов полей всех этих зарядов.
Работа совершаемая силами электростатического поля при перемещении заряда из точки 1 в точку 2 может быть представлена как
Работа равна произведению перемещаемого заряда на разность потенциалов в начальной и конечной точках.

РАЗНОСТЬ ПОТЕНЦИАЛОВ
Разность потенциалов двух точек 1 и 2 в электростати-ческом поле определяется работой, совершаемой си-лами поля при перемещении единичного положи-тельного заряда из точки 1 в точку 2.
Интегрирование можно проводить вдоль любой линии соединяющей начальную и конечную точки, так как здесь работа не зависит от траектории.
Если перемещать заряд из произвольной точки за пре-делы поля (в бесконечность), где потенциал равен ну-лю , то работа сил электростатического поля :

ПОТЕНЦИАЛ
ПОТЕНЦИАЛ – физическая величина, определяемая ра-ботой по перемещению единичного положительного заряда при удалении его из данной точки в бесконеч-ность.
Эта работа численно равна работе совершаемой внеш-ними силами (против сил электростатического поля), по перемещению единичного положительного заряда из бесконечности в данную точку.
Единица потенциала : вольт.
1 вольт – потенциал такой точки поля в которой заряд в 1 Кл обладает потенциальной энергией 1 Дж.
1 В=1 Дж/Кл

ЭКВИПОТЕНЦИАЛЬНЫЕ ПОВЕРХНОСТИ
ВЗАИМОСВЯЗЬ МЕЖДУ НАПРЯЖЕННОСТЬЮ И ПОТЕНЦИАЛОМ

ВЗАИМОСВЯЗЬ МЕЖДУ НАПРЯЖЕННОСТЬЮ И ПОТЕНЦИАЛОМ
Напряженность Е – СИЛОВАЯ характеристика электро-статического поля
Потенциал ϕ – ЭНЕРГЕТИЧЕСКАЯ характеристика элек-тростатического поля
Найдём взаимосвязь между характеристиками электро-статического поля.
Работа по перемещению единичного положительного заряда вдоль оси , если точки расположены беско-нечно близко друг к другу и ,будет равна , та же работа равна .

Где: -символ частной производной, показывает, что дифференцирование производится только по х.
Повторим аналогичные рассуждения для осей y и z можно найти вектор в трёхмерном пространстве.
Где - орты, (единичные векторы осей x,y,z) .
Напряженность электростатического поля равна гради-енту потенциала, взятому со знаком минус.
Градиент потенциала:
Знак – определяется тем, что вектор напряженности электростатического поля направлен в сторону убы-вания потенциала.

ЭКВИПОТЕНЦИАЛЬНЫЕ ПОВЕРХНОСТИ
Для графического изображения распреде-ления потенциала электростатического поля используют эквипотенциальные поверхности – поверхности, во всех точ-ках которых, потенциал ϕ имеет одно и
тоже значение.
Если поле создается точечным зарядом, то в этом случае эквипотенциальные поверхности являются концентри-ческими сферами.
Линии напряженности – радиальные прямые. Следова-тельно, линии напряженности в случае точечного заря-да перпендикулярны эквипотенциальным поверхнос-тям.
ϕ₁
ϕ₂
q

Линии напряженности всегда нормальны к эквипотен-циальным поверхностям.
Все точки эквипотенциальной поверхности имеют оди-наковый потенциал, и работа по перемещению заря-да вдоль этой поверхности равна нулю.
Значит, электростатические силы, действующие на за-ряд, всегда направлены по нормали к эквипотенци-альным поверхностям. Следовательно, вектор всег-да нормален к эквипотенциальной поверхности, а поэтому линии вектора ортогональны этим поверх-ностям.

ВЫЧИСЛЕНИЕ РАЗНОСТИ ПОТЕНЦИАЛОВ ПО НАПРЯЖЕННОСТИ ПОЛЯ

1. ПОЛЕ РАВНОМЕРНО ЗАРЯЖЕННОЙ БЕСКОНЕЧНОЙ ПЛОСКОСТИ
Напряженность данного поля опреде-
ляется формулой:
Тогда разность потенциалов в точках 1 и 2 :

2.ПОЛЕ ДВУХ БЕСКОНЕЧНЫХ, ПАРАЛЛЕЛЬНЫХ, РАЗНОИМЕННО ЗАРЯЖЕННЫХ ПЛОСКОСТЕЙ
Напряженность определяется формулой
Расстояние между плоскостями d.
Разность потенциалов между плоскос-
тями:
d

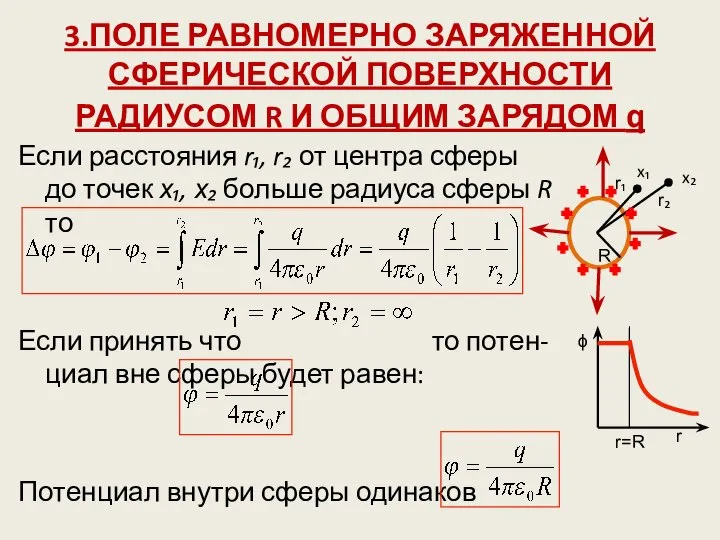
3.ПОЛЕ РАВНОМЕРНО ЗАРЯЖЕННОЙ СФЕРИЧЕСКОЙ ПОВЕРХНОСТИ РАДИУСОМ R И ОБЩИМ ЗАРЯДОМ q
Если расстояния r₁, r₂ от центра сферы до точек х₁, х₂ больше радиуса сферы R то
Если принять что то потен-циал вне сферы будет равен:
Потенциал внутри сферы одинаков
x₁
x₂

4.ПОЛЕ ОБЪЕМНО ЗАРЯЖЕННОГО ШАРА РАДИУСА R, С ОБЩИМ ЗАРЯДОМ q
Вне шара разность потенциалов определяется
аналогично предыдущему случаю:
Внутри шара (r'
Разность потенциалов для точек внутри шара:

5. ПОЛЕ РАВНОМЕРНО ЗАРЯЖЕННОГО БЕСКОНЕЧНОГО ЦИЛИНДРА РАДИУСА R C ЛИНЕЙНОЙ ПЛОТНОСТЬЮ τ
Вне цилиндра (r>R) напряженность равна
Следовательно, разность потенциалов:

ВЕЩЕСТВО В ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ

ДИЭЛЕКТРИК В ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ
ПОЛЯРИЗАЦИЯ ДИЭЛЕКТРИКА

Диэлектрики – вещества, при обычных условиях не про-водящие электрический ток.
Все молекулы и атомы диэлектрика электрически нейт-ральны (положительный заряд ядра атома равен от-рицательному заряду электронов атома и суммарный заряд атома равен нулю). Однако молекулы обладают электрическими свойствами.
Если заменить положительный заряд ядер атомов мо-лекул суммарным зарядом +q ,а заряд всех электро-нов суммарным отрицательным зарядом –q, находя-щемся в «центре тяжести» отрицательных зарядов, то молекулу можно рассматривать как электрический диполь с электрическим моментом ( -суммар-ный положительный заряд ядер, -вектор проведен-ный из «центра тяжести» электронов к протонам.

В диэлектриках нет свободных носителей заряда (заря-женных частиц, которые могли бы прийти под воз-действием электрического поля в упорядоченное дви-жение и организовать электрический ток.
Диэлектриками являются:
Все газы (если они не подверглись ионизации)
Некоторые жидкости (дистиллированная вода, бензол и масла (нефтяные и растительные)
Твердые тела (стекло, фарфор, слюда и т.п.)
Удельное электрическое сопротивление диэлектриков
Ом*м, ( у металлов Ом*м).

ТИПЫ ДИЭЛЕКТРИКОВ

ПЕРВАЯ ГРУППА
(N₂, H₂, O₂, CO₂…) – вещества молекулы которых имеют симметричное строение, то есть «центры тяжести» положительных и отрицательных зарядов в отсутст-вие внешнего электрического поля совпадают и дипольный момент молекулы равен нулю . Молекулы таких диэлектриков называют неполярны-ми. Под действием внешнего электрического поля за-ряды неполярных молекул смещаются в противопо-ложные стороны (положительные по полю, отрица-тельные против) и молекула приобретает дипольный момент.

ВТОРАЯ ГРУППА
(H₂O, NH₃, SO₂ CO…) – вещества молекулы которых име-ют асимметричное строение , то есть «центры тяжес-ти» положительных и отрицательных зарядов не сов-падают. Эти молекулы и в отсутствие внешнего элект-рического поля обладают дипольным моментом. Мо-лекулы таких диэлектриков называются полярными. При отсутствии внешнего электрического поля, ди-польные моменты полярных молекул вследствие теп-лового движения ориентированы хаотично и их ре-зультирующий момент равен нулю. Если такой диэ-лектрик поместить во внешнее электрическое поле, то силы этого поля будут стремиться повернуть диполи вдоль поля, и возникает, отличный от нуля, электри-ческий момент.

ТРЕТЬЯ ГРУППА
(NₐCL, KCL) – Вещества, молекулы которых имеют ионное строение. Ионные кристаллы представляют собой про-странственные решетки с правильным чередованием ионов различных знаков. В этих кристаллах нельзя вы-делять отдельные молекулы, и рассматривать их мож-но как систему двух вдвинутых одна в другую ионных подрешеток. При наложении на ионный кристалл элек-трического поля происходит некоторая деформация кристаллической решетки или относительное смеще-ние подрешеток, приводящее к возникновению дипольных моментов.

ПОЛЯРИЗАЦИЯ ДИЭЛЕКТРИКОВ
ТИПЫ ПОЛЯРИЗАЦИИ
ПОЛЯРИЗОВАННОСТЬ

Внесение всех трёх групп диэлектриков во внешнее эле-ктростатическое поле приводит к возникновению от-личного от нуля результирующего момента диэлект-рика, или иначе к ПОЛЯРИЗАЦИИ ДИЭЛЕКТРИКА.
ПОЛЯРИЗАЦИЯ ДИЭЛЕКТРИКА – процесс ориентации ди-полей или появления под воздействием электричес-кого поля ориентированных по полю диполей.
В зависимости от строения молекул (атомов) диэлектри-ка (соответственно 3 группам диэлектриков) различа-ют 3 типа поляризации:
Электронная поляризация
Ориентационная поляризация
Ионная поляризация

1. Электронная (деформационная) поляризация
Осуществляется у неполярных диэлектриков. Под дейс-твием внешнего электрического поля возникают на-веденные (индуцированные) дипольные моменты направленные вдоль поля,(по направлению ). Теп-ловое движение молекул не влияет на электронную поляризацию. В газообразных и жидких полярных диэлектриках происходит одновременно с ориента-ционной.

2. Ориентационная поляризация
Наблюдается у полярных диэлектриков. Внешнее элек-трическое поле стремится ориентировать дипольные моменты полярных молекул-диполей по направле-нию вектора . Этому препятствует хаотическое дви-жение молекул, вызывающее беспорядочный раз-брос диполей. В итоге совместного действия электри-ческого поля и теплового движения, возникает преи-мущественная ориентация дипольных электрических моментов вдоль поля, возрастающая с увеличением напряженности электрического поля, и с уменьшени-ем температуры.

3. Ионная поляризация
Возникает в твердых диэлектриках имеющих ионную кристаллическую решетку. Внешнее электрическое поле вызывает в таких диэлектриках смещение всех положительных ионов в направлении напряженнос-ти поля , а всех отрицательных ионов в противопо-ложную сторону. Происходит смещение подрешеток приводящее к возникновению дипольных моментов.

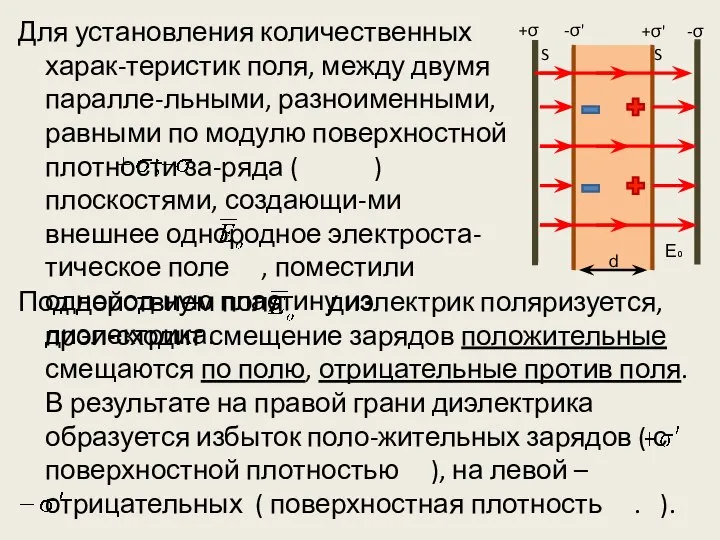
ПОЛЯРИЗОВАННОСТЬ
При помещении диэлектрика во внешнее электростати-ческое поле он поляризуется, то есть приобретает отличный от нуля дипольный момент
- дипольный момент одной молекулы.
Количественной мерой поляризации служит:
Поляризованность (вектор поляризации) - дипольный момент единицы объема диэлектрика.
В пределах малого объема все молекулы неполярного диэлектрика приобретают в электрическом поле оди-

наковые индуцированные электрические моменты .
Поляризованность неполярного диэлектрика равна:
- концентрация молекул.
Принято считать что поляризованность линейно зави-сит от напряженности поля . Если не очень ве-лико то:
- диэлектрическая восприимчивость вещества
- безразмерная величина характеризующая свойства диэлектрика ( значение для диэлектриков обычно несколько единиц, но бывает и выше (для во-ды ,для спирта )).

Для установления количественных харак-теристик поля, между двумя паралле-льными, разноименными, равными по модулю поверхностной плотности за-ряда ( ) плоскостями, создающи-ми внешнее однородное электроста-тическое поле , поместили однород-ную пластину из диэлектрика.
Под действием поля диэлектрик поляризуется, прои-сходит смещение зарядов положительные смещаются по полю, отрицательные против поля. В результате на правой грани диэлектрика образуется избыток поло-жительных зарядов ( с поверхностной плотностью ), на левой – отрицательных ( поверхностная плотность . ).

Эти нескомпенсированные заряды, появляющиеся в ре-зультате поляризации диэлектрика называются свя-занными. Так как , то не всё поле компенси-руется полем зарядов диэлектрика, часть линий нап-ряженности пройдет сквозь диэлектрик, другая часть обрывается на связанных зарядах. Следовательно, поляризация диэлектрика вызывает в нём уменьше-ние поля, по сравнению с первоначальным. Вне диэлектрика .
Появление связанных зарядов приводит к возникнове-нию дополнительного электрического поля (вызы-ваемого связанными зарядами), направленного про-тив внешнего поля (созданного свободными заря-дами) и ослабляет его.

Диэлектрическая проницаемость вещества
Результирующее поле внутри диэлектрика:
Так как создаётся разноименными плоскостями с по-верхностной плотностью то
Определим поверхностную плотность связанных зарядов
Полный дипольный момент пластинки диэлектрика:
- площадь грани пластинки диэлектрика
- толщина диэлектрика
- заряд на каждой грани диэлектрика

Поверхностная плотность связанных зарядов равна поляризованности . Из этого следует:
Напряженность результирующего поля внутри диэлект-рика равна:
- диэлектрическая проницаемость, безразмерная ве-личина, показывающая во сколько раз поле ослабля-ется диэлектриком, характеризует количественное свойство диэлектрика поляризоваться в электричес-ком поле.

ЭЛЕКТРИЧЕСКОЕ СМЕЩЕНИЕ ТЕОРЕМА ОСТРОГРАДСКОГО – ГАУССА ДЛЯ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ В ДИЭЛЕКТРИКЕ

ЭЛЕКТРИЧЕСКОЕ СМЕЩЕНИЕ
Напряженность электростатического поля зависит от свойств среды. В однородной среде обратно про-порционально . Вектор , переходя через границу диэлектриков, испытывает скачкообразное измене-ние. Для удобства расчетов, необходимо помимо век-тора напряженности охарактеризовать электрическое поле вектором электрического смещения .
Единица электрического смещения Кл/м²

Связанные заряды появляются в диэлектрике при нали-чии внешнего электростатического поля создаваемого системой свободных зарядов, то есть в диэлектрике на электростатическое поле свободных зарядов нак-ладывается дополнительное поле связанных зарядов.
Результирующее поле описывается вектором напряжен-ности и зависит от свойств диэлектрика.
Вектором описывается электростатическое поле соз-даваемое свободными зарядами . Связанные заряды возникающие в диэлектрике могут, однако, вызвать перераспределение свободных зарядов создающих поле. Поэтому характеризует электростатическое поле создаваемое свободными зарядами (в вакууме), но при таком их распределении в пространстве, кото-рое имеется при наличии диэлектрика.

Подобно , изображается с помощью линий элект-рического смещения, направление и густота которых определяются так же как и для линий напряженности.
Отличие в том, что линии вектора могут начинаться и заканчиваться на любых (свободных и связанных) за-рядах, а линии вектора только на свободных заря-дах. Через области поля, где находятся связанные за-ряды, линии вектора проходят не прерываясь.

ТЕОРЕМА ОСТРОГРАДСКОГО – ГАУССА ДЛЯ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ В ДИЭЛЕКТРИКЕ
Для произвольной замкнутой поверхности S поток векто-ра электрического смещения сквозь эту поверх-ность равен:
Теорема Остроградского-Гаусса для электростатического поля в диэлектрике имеет вид:
Поток вектора смещения электростатического поля в диэ-лектрике сквозь произвольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности свободных электрических зарядов.

В данной форме теорема Гаусса справедлива для элект-ростатического поля как для однородных , так и для неоднородных сред.
В случае вакуума (ε=1) выполняется условие , тогда поток вектора напряженности сквозь произ-вольную замкнутую поверхность равен
Так как источниками поля в среде являются как свобо-дные, так и связанные заряды, то теорему Гаусса для поля в самом общем виде можно записать: