Содержание
- 2. * Лекции проф. П.Ю.Гуляева Геометрическая оптика Оптика- это раздел физики, который изучает природу света, световые явления
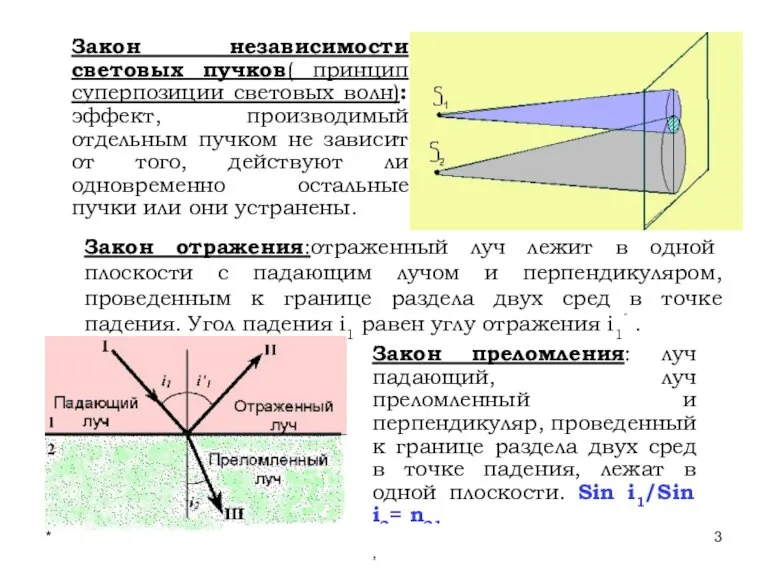
- 3. * Лекции проф. П.Ю.Гуляева Закон независимости световых пучков( принцип суперпозиции световых волн): эффект, производимый отдельным пучком
- 4. * Лекции проф. П.Ю.Гуляева Он равен отношению абсолютных показателей преломления двух сред: n21=n2/n1 n1Sin i1=n2Sin i2
- 5. * Лекции проф. П.Ю.Гуляева 2.Полное отражение. Если свет распространяется из среды с большим показателем преломления n1
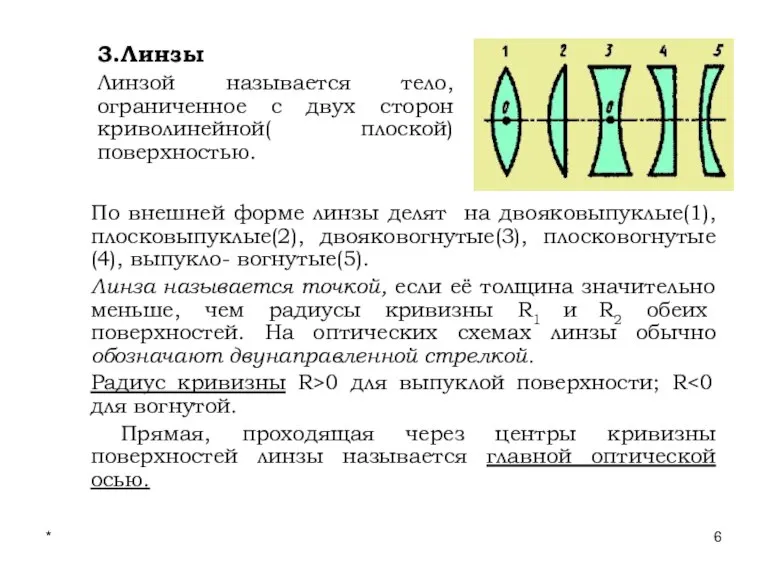
- 6. * Лекции проф. П.Ю.Гуляева 3.Линзы Линзой называется тело, ограниченное с двух сторон криволинейной( плоской) поверхностью. По
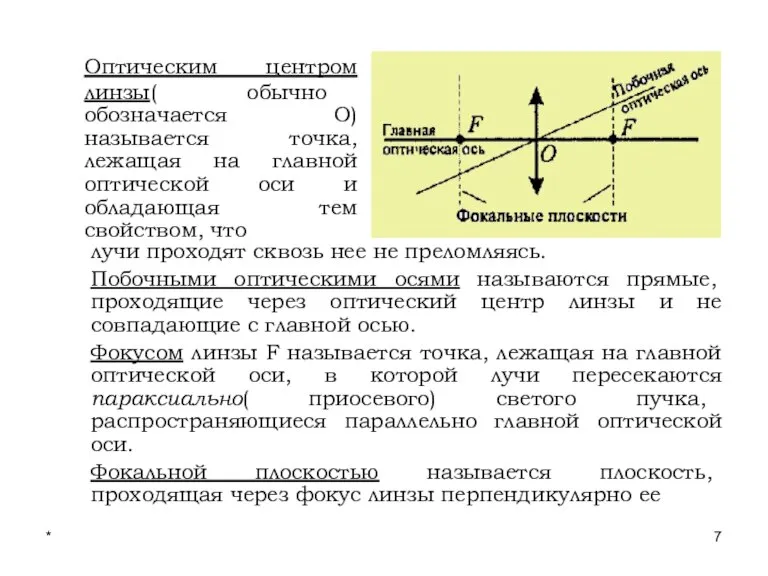
- 7. * Лекции проф. П.Ю.Гуляева Оптическим центром линзы( обычно обозначается О) называется точка, лежащая на главной оптической
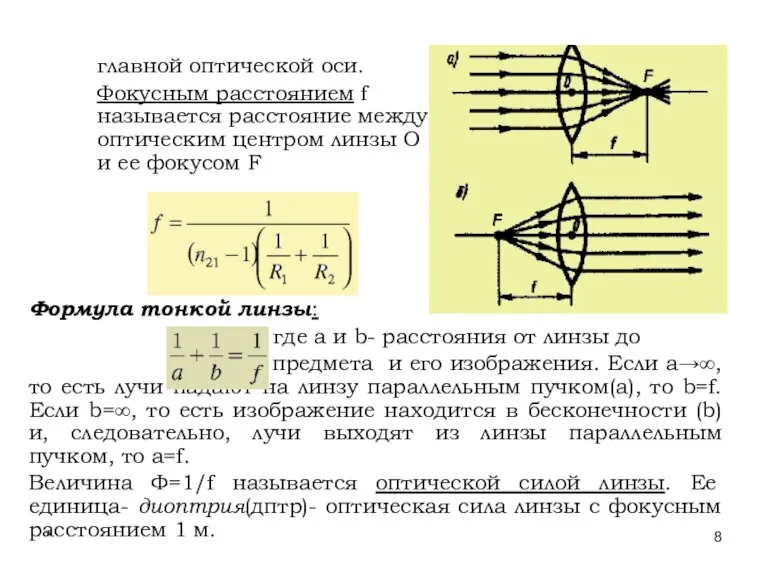
- 8. * Лекции проф. П.Ю.Гуляева Формула тонкой линзы: , где a и b- расстояния от линзы до
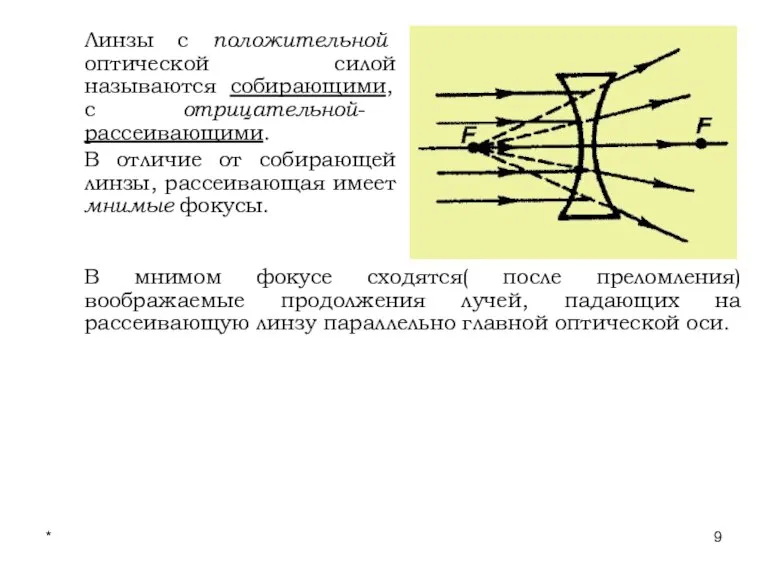
- 9. * Лекции проф. П.Ю.Гуляева Линзы с положительной оптической силой называются собирающими, с отрицательной- рассеивающими. В отличие
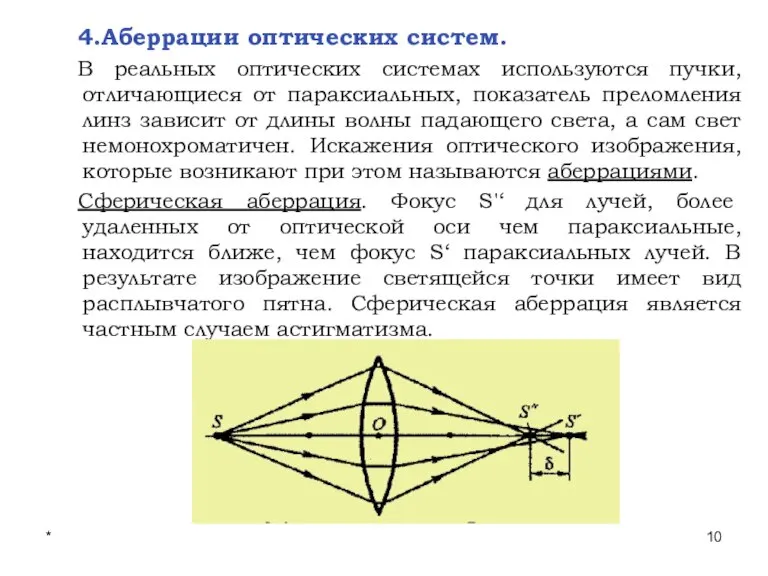
- 10. * Лекции проф. П.Ю.Гуляева 4.Аберрации оптических систем. В реальных оптических системах используются пучки, отличающиеся от параксиальных,
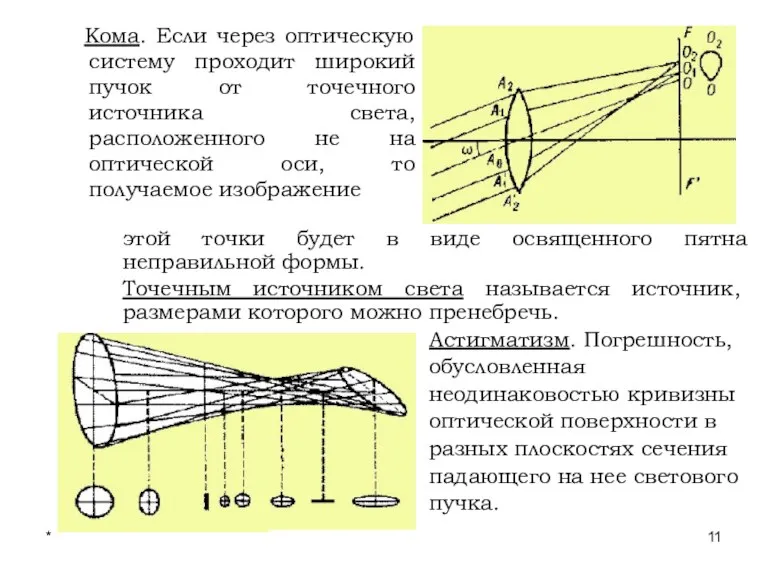
- 11. * Лекции проф. П.Ю.Гуляева Кома. Если через оптическую систему проходит широкий пучок от точечного источника света,
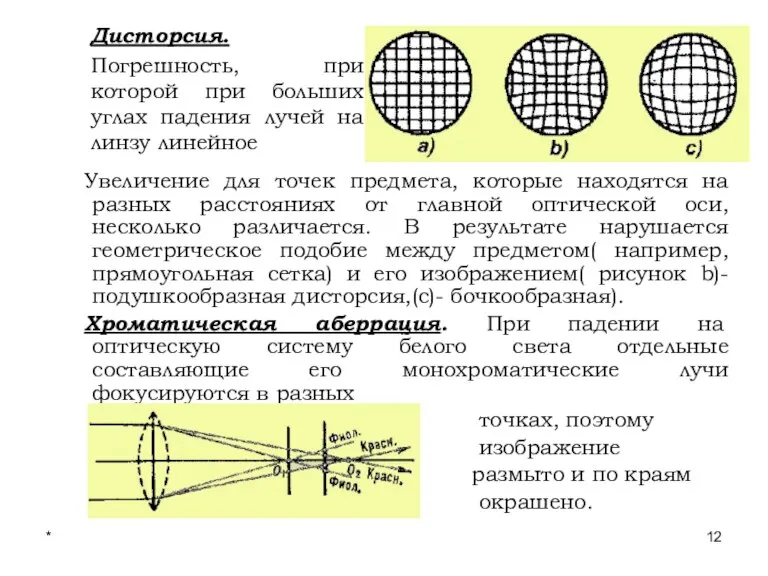
- 12. * Лекции проф. П.Ю.Гуляева Дисторсия. Погрешность, при которой при больших углах падения лучей на линзу линейное
- 13. * Лекции проф. П.Ю.Гуляева 5.Энергетические величины в фотометрии Фотометрия- раздел оптики, в котором рассматриваются энергетические характеристики
- 14. * Лекции проф. П.Ю.Гуляева Энергетическая сила света(сила излучения) IЕ – величина, равная отношению потока излучения ФЕ
- 15. * Лекции проф. П.Ю.Гуляева 6.Световые величины в фотометрии. Основной световой единицей в СИ является единица силы
- 16. * Лекции проф. П.Ю.Гуляева Единица яркости- кандела на метр в квадрате( кд/ м2) . Вϕ= I/
- 17. * Лекции проф. П.Ю.Гуляева Интерференция света 7.Принцип Гюйгенса Волновая теория основывается на принципе Гюйгенса: каждая точка,
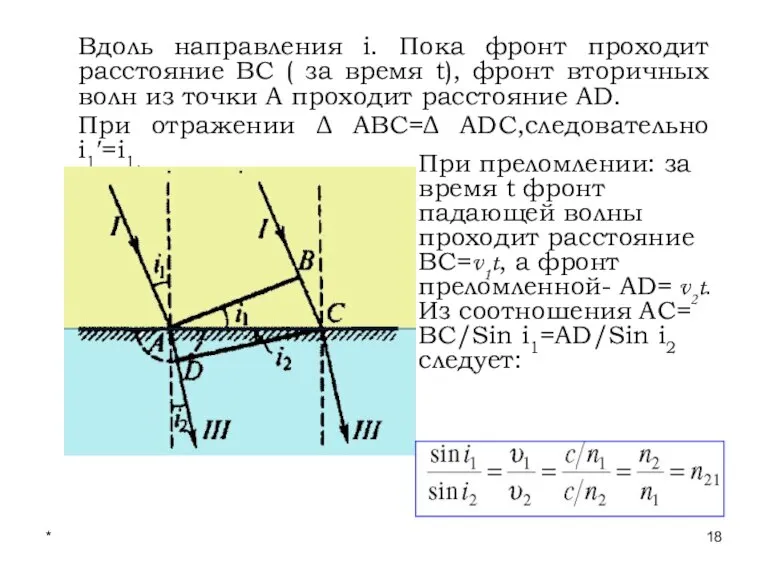
- 18. * Лекции проф. П.Ю.Гуляева Вдоль направления i. Пока фронт проходит расстояние ВС ( за время t),
- 19. * Лекции проф. П.Ю.Гуляева 8.Когерентность Когерентностью называется согласованное протекание во времени и пространстве нескольких колебательных или
- 20. * Лекции проф. П.Ю.Гуляева Если волна распространяется в однородной среде, то фаза колебаний в определенной точке
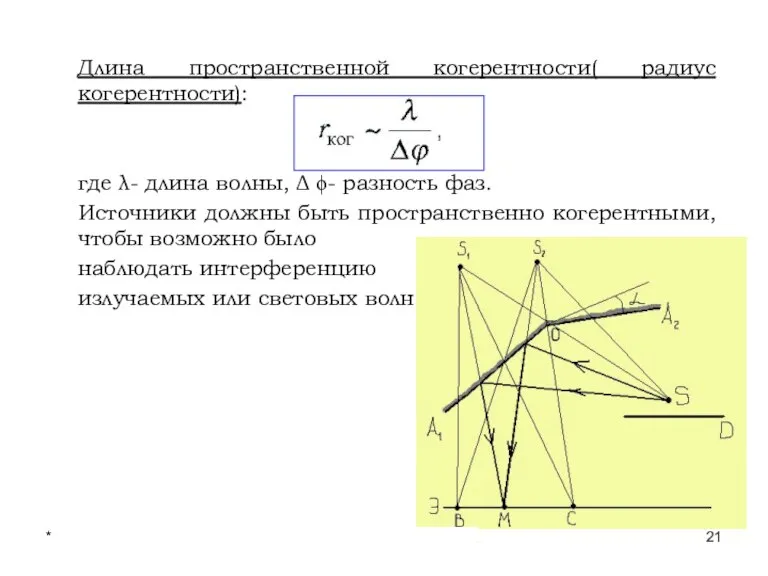
- 21. * Лекции проф. П.Ю.Гуляева Длина пространственной когерентности( радиус когерентности): где λ- длина волны, Δ ϕ- разность
- 22. * Лекции проф. П.Ю.Гуляева 9. Интерференция света. Интерференция света- сложение в пространстве двух или нескольких когерентных
- 23. * Лекции проф. П.Ю.Гуляева Разность фаз δ колебаний, возбуждаемых в точке М, равна: Произведение геометрической длины
- 24. * Лекции проф. П.Ю.Гуляева Условие интерференционного минимума. Если оптическая разность хода Δ равна нечетному числу полуволн,
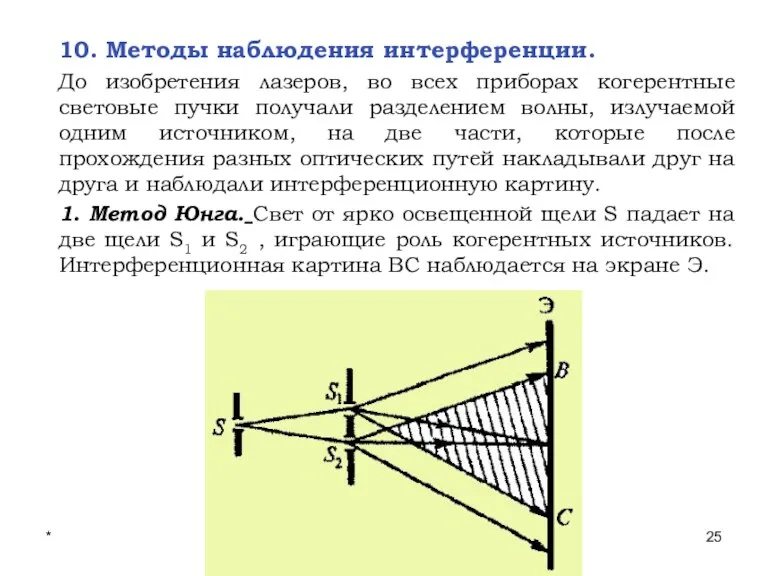
- 25. * Лекции проф. П.Ю.Гуляева 10. Методы наблюдения интерференции. До изобретения лазеров, во всех приборах когерентные световые
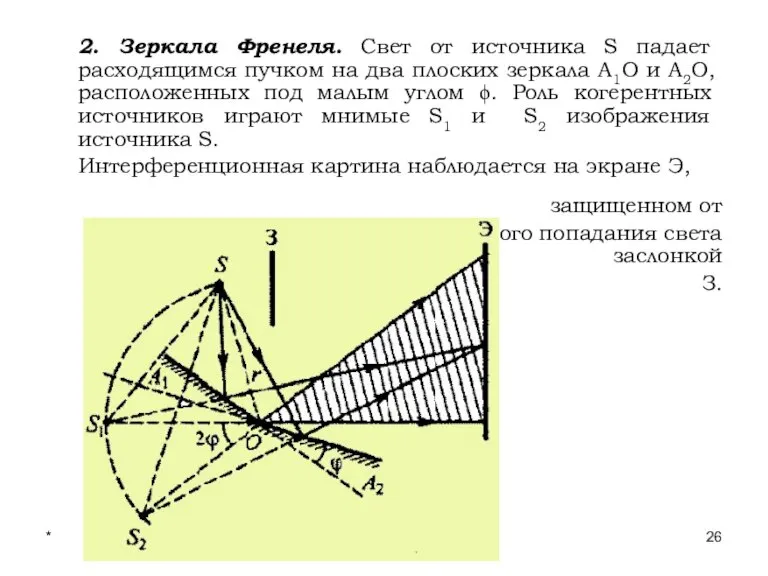
- 26. * Лекции проф. П.Ю.Гуляева 2. Зеркала Френеля. Свет от источника S падает расходящимся пучком на два
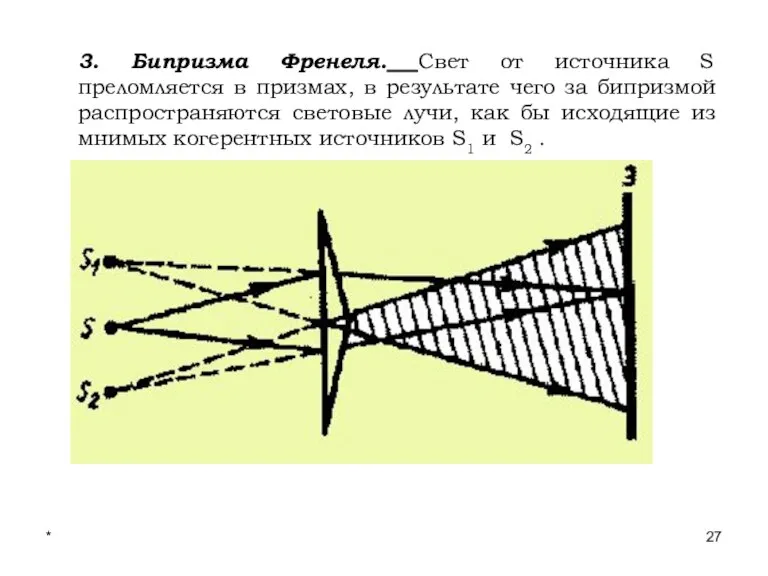
- 27. * Лекции проф. П.Ю.Гуляева 3. Бипризма Френеля. Свет от источника S преломляется в призмах, в результате
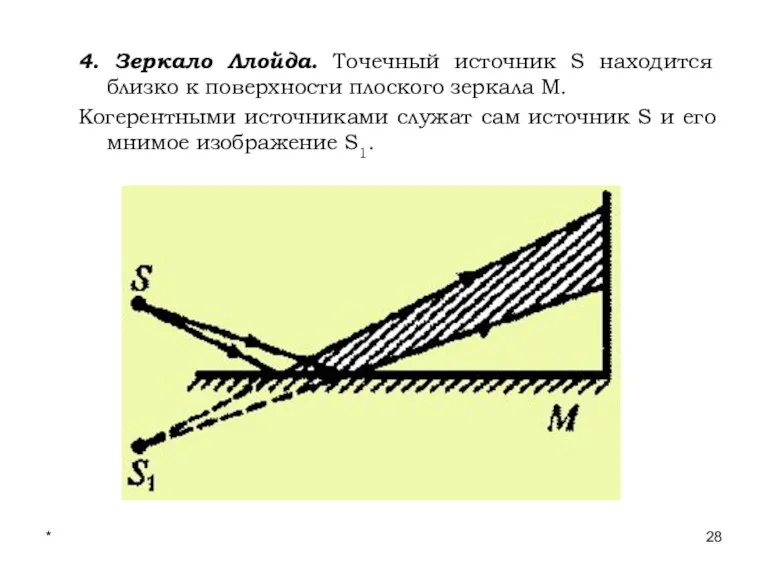
- 28. * Лекции проф. П.Ю.Гуляева 4. Зеркало Ллойда. Точечный источник S находится близко к поверхности плоского зеркала
- 29. * Лекции проф. П.Ю.Гуляева 11. Расчет интерференционной картины от двух щелей. Две щели S1 и S2
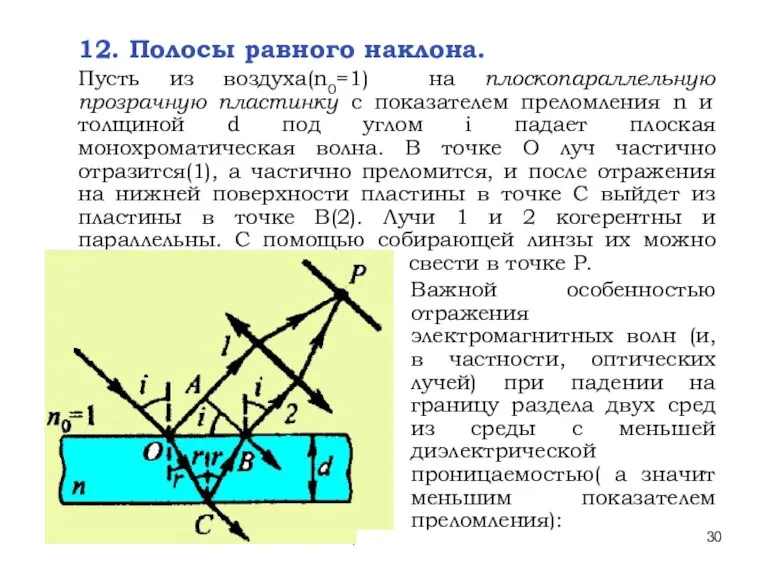
- 30. * Лекции проф. П.Ю.Гуляева 12. Полосы равного наклона. Пусть из воздуха(n0=1) на плоскопараллельную прозрачную пластинку с
- 31. * Лекции проф. П.Ю.Гуляева При отражении света от более плотной среды( n0 С учетом этого, оптическая
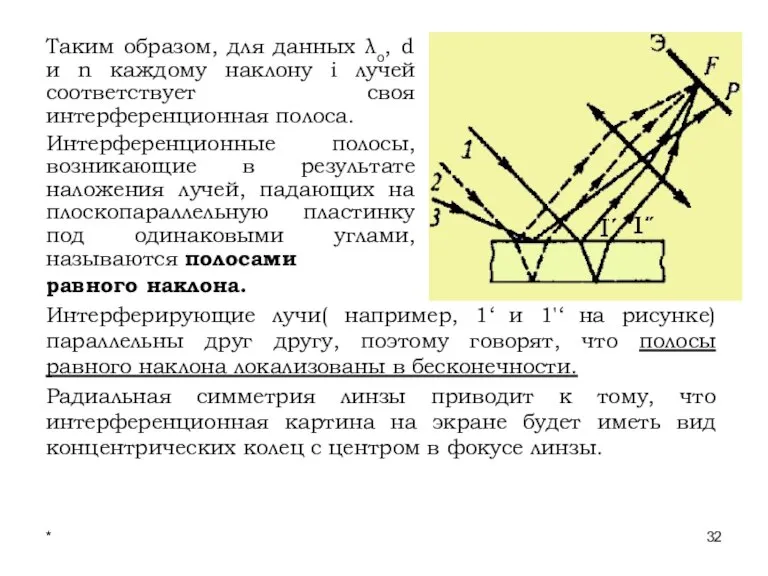
- 32. * Лекции проф. П.Ю.Гуляева Таким образом, для данных λо, d и n каждому наклону i лучей
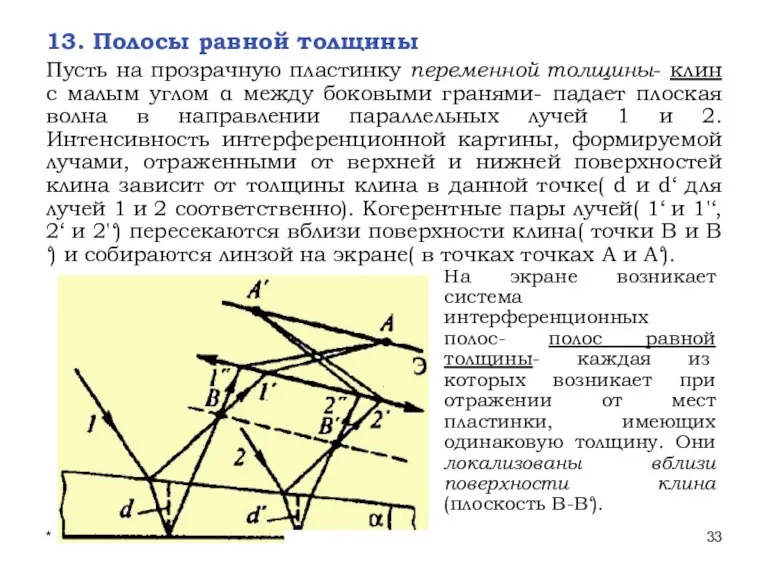
- 33. * Лекции проф. П.Ю.Гуляева 13. Полосы равной толщины Пусть на прозрачную пластинку переменной толщины- клин с
- 34. * Лекции проф. П.Ю.Гуляева 14. Кольца Ньютона Кольца Ньютона наблюдаются при отражении света от воздушного зазора,
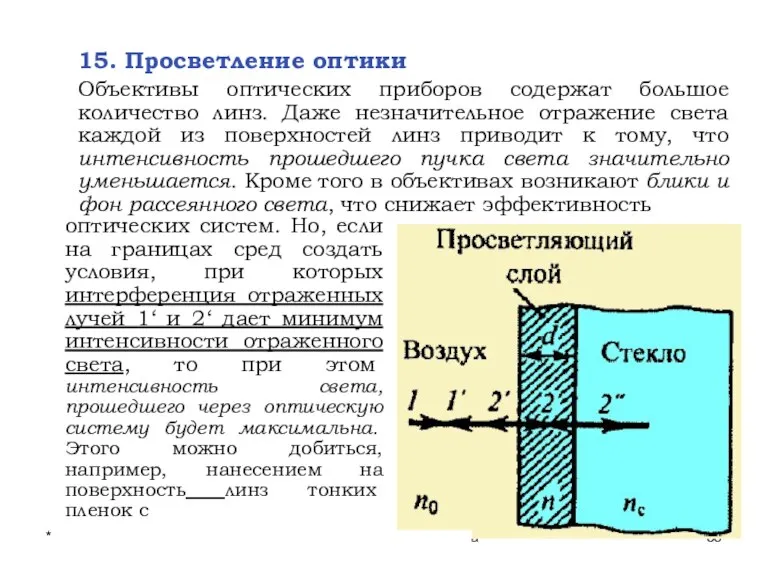
- 35. * Лекции проф. П.Ю.Гуляева 15. Просветление оптики Объективы оптических приборов содержат большое количество линз. Даже незначительное
- 36. * Лекции проф. П.Ю.Гуляева показателем преломления no В этом случае амплитуды когерентных лучей 1‘ и 2'‘
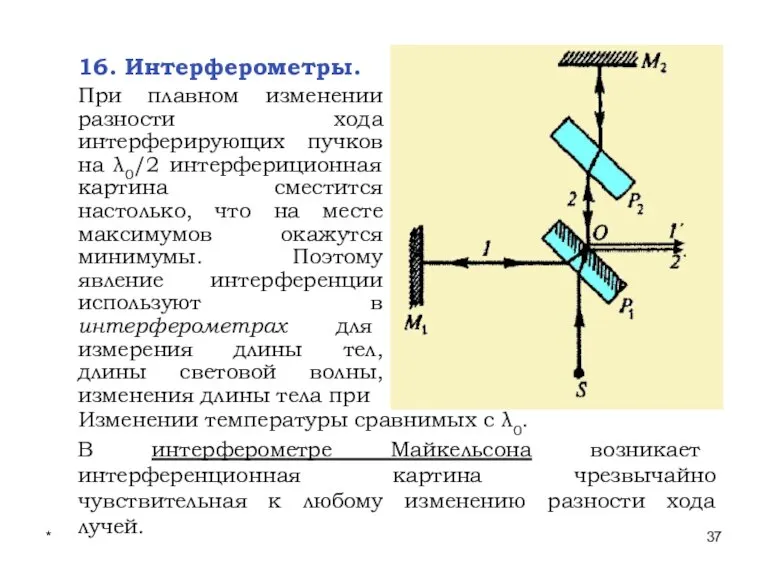
- 37. * Лекции проф. П.Ю.Гуляева 16. Интерферометры. При плавном изменении разности хода интерферирующих пучков на λ0/2 интерфериционная
- 38. * Лекции проф. П.Ю.Гуляева Дифракция света 17.Принцип Гюйгенса- Френеля Дифракция – это огибание волнами препятствий, встречающихся
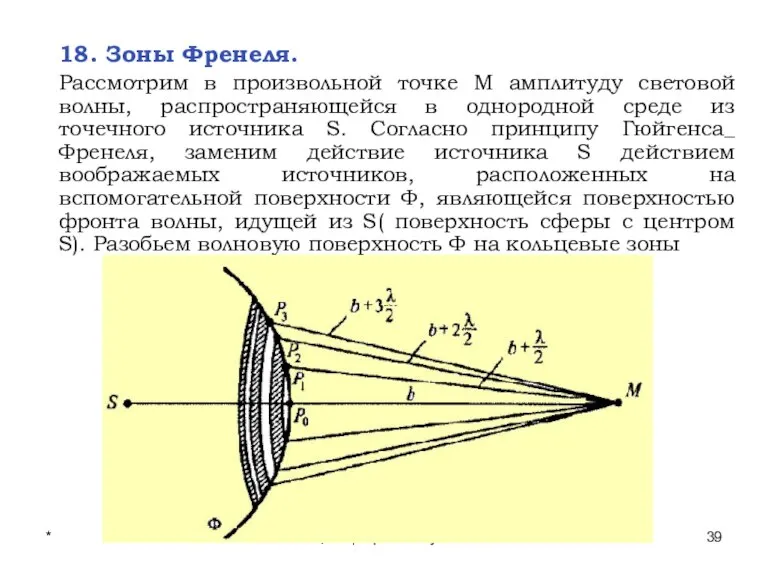
- 39. * Лекции проф. П.Ю.Гуляева 18. Зоны Френеля. Рассмотрим в произвольной точке М амплитуду световой волны, распространяющейся
- 40. * Лекции проф. П.Ю.Гуляева Такого размера, чтобы расстояние от краев зоны до М отличались на λ/2.
- 41. * Лекции проф. П.Ю.Гуляева Распространение света от S к М происходит так, будто световой поток распространяется
- 42. * Лекции проф. П.Ю.Гуляева 19. Дифракция в сходящихся лучах. Дифракция в сходящихся лучах( дифракция Френеля)- это
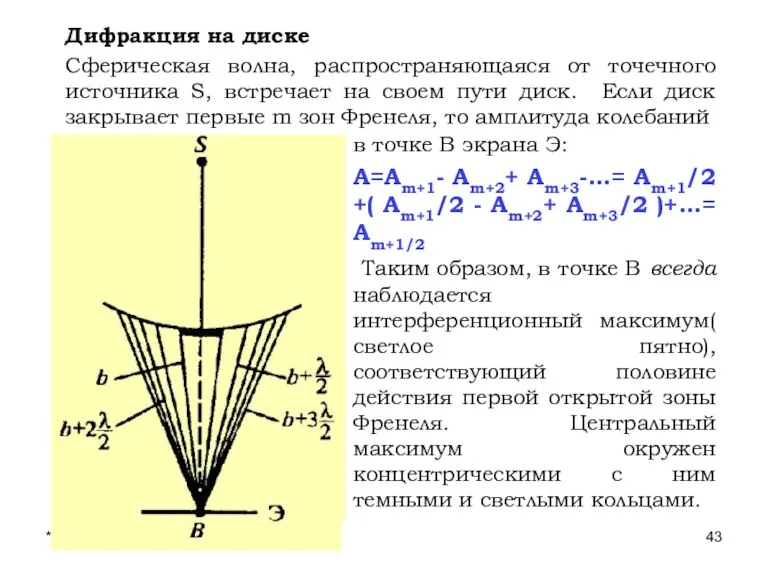
- 43. * Лекции проф. П.Ю.Гуляева Дифракция на диске Сферическая волна, распространяющаяся от точечного источника S, встречает на
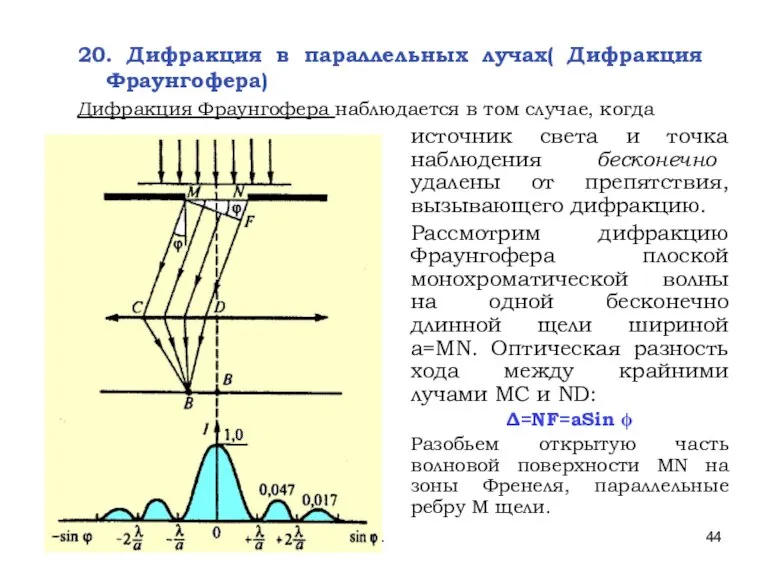
- 44. * Лекции проф. П.Ю.Гуляева 20. Дифракция в параллельных лучах( Дифракция Фраунгофера) Дифракция Фраунгофера наблюдается в том
- 45. * Лекции проф. П.Ю.Гуляева Ширина каждой зоны выбирается так, чтобы разность хода от краев этих зон
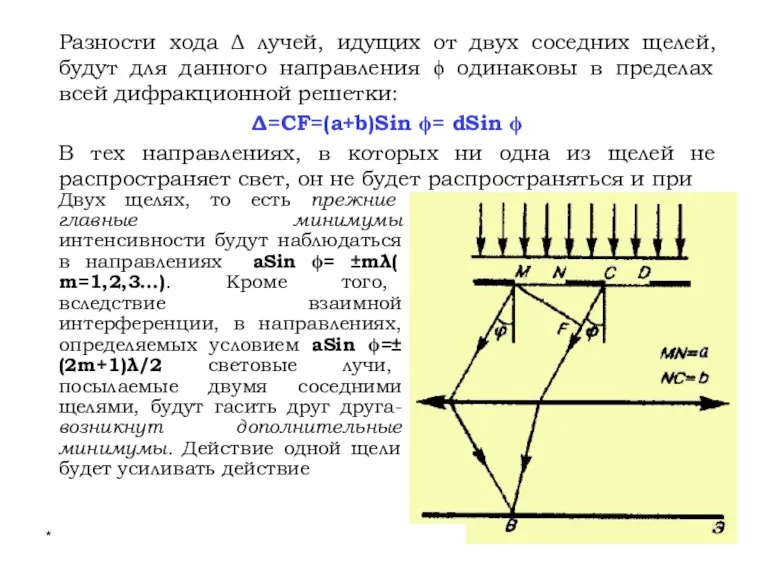
- 46. * Лекции проф. П.Ю.Гуляева 21. Дифракция Фраунгофера на дифракционной решетке. Одномерная дифракционная решетка- система параллельных щелей
- 47. * Лекции проф. П.Ю.Гуляева Двух щелях, то есть прежние главные минимумы интенсивности будут наблюдаться в направлениях
- 48. * Лекции проф. П.Ю.Гуляева Другой, если aSin ϕ= ±2mλ/2 ( m=1,2,3…)- условие главных максимумов. Между двумя
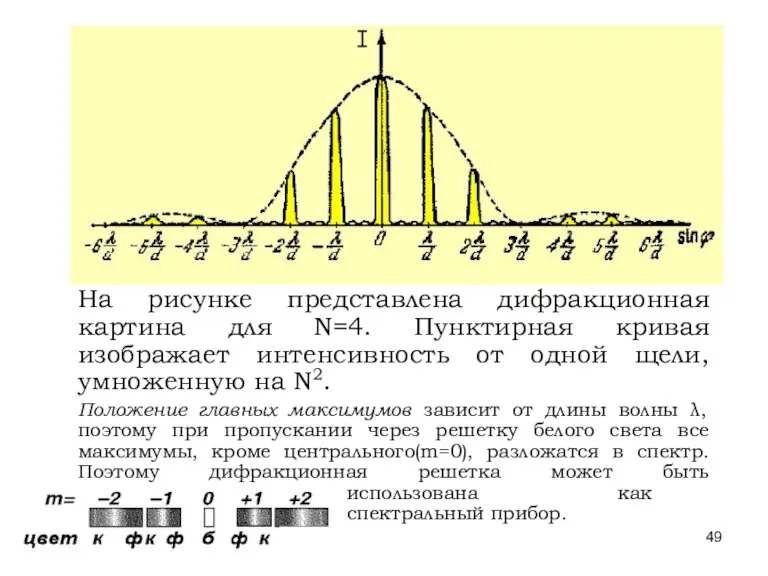
- 49. * Лекции проф. П.Ю.Гуляева На рисунке представлена дифракционная картина для N=4. Пунктирная кривая изображает интенсивность от
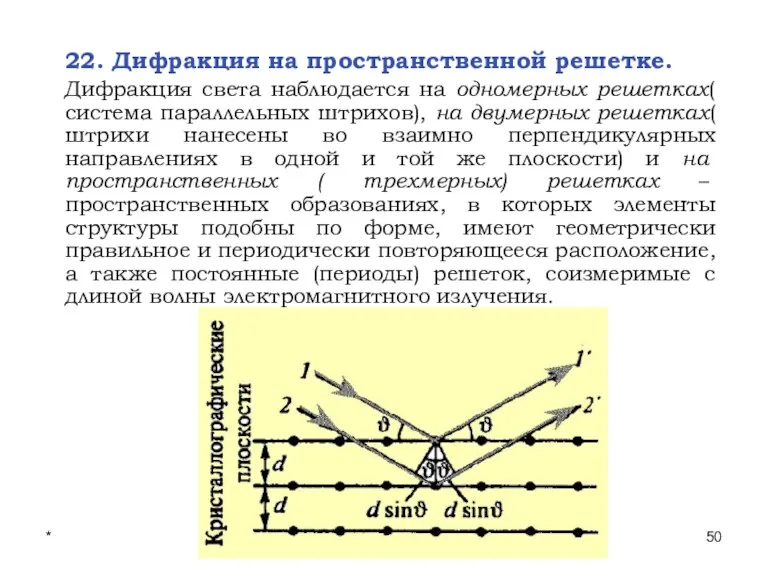
- 50. * Лекции проф. П.Ю.Гуляева 22. Дифракция на пространственной решетке. Дифракция света наблюдается на одномерных решетках( система
- 51. * Лекции проф. П.Ю.Гуляева Для наблюдения дифракции рентгеновского излучения могут быть использованы кристаллы: представим кристалл в
- 52. * Лекции проф. П.Ю.Гуляева 23. Разрешающая способность спектрального прибора. Критерии Релея- изображения двух близлежащих одинаковых точечных
- 53. * Лекции проф. П.Ю.Гуляева Разрешающей способностью спектрального прибора называют безразмерную величину R= λ⁄δλ ,где δλ-абсолютное значение
- 54. * Лекции проф. П.Ю.Гуляева 24. Разрешающая способность дифракционной решетки. Пусть максимум m-го порядка для длины волны
- 55. * Лекции проф. П.Ю.Гуляева Взаимодействие света с веществом 25. Дисперсия света Дисперсия света – это зависимость
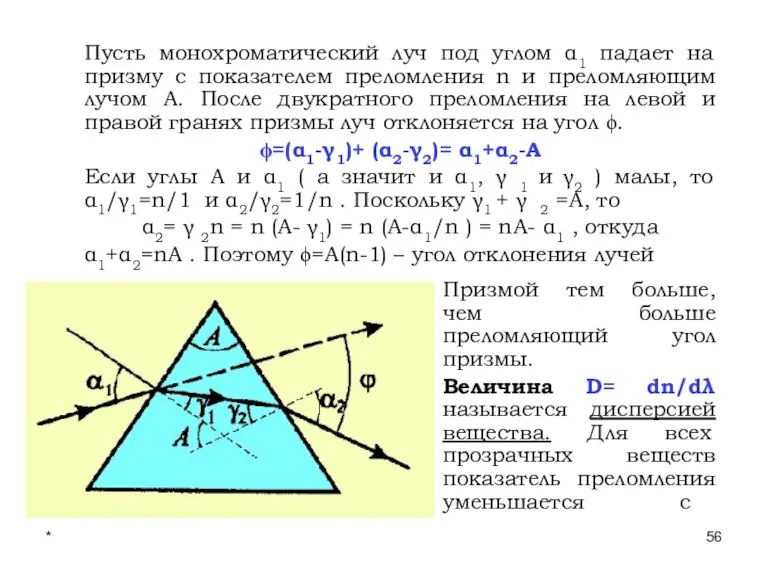
- 56. * Лекции проф. П.Ю.Гуляева Пусть монохроматический луч под углом α1 падает на призму с показателем преломления
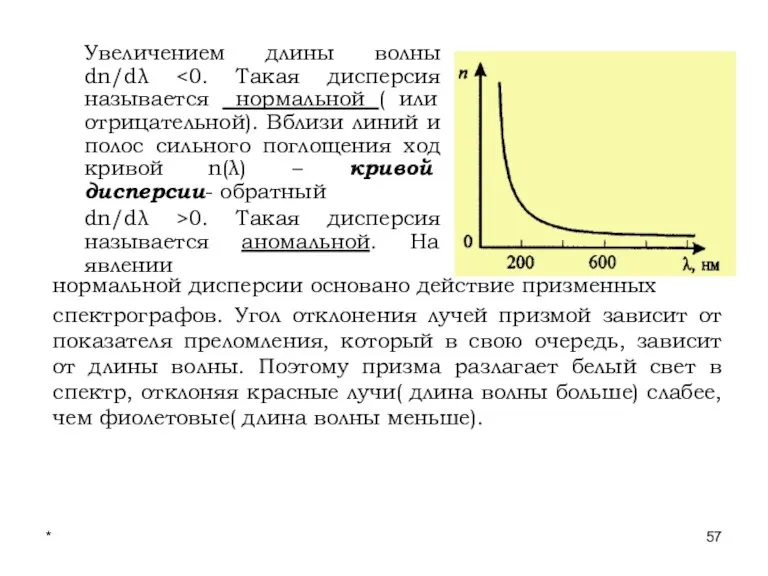
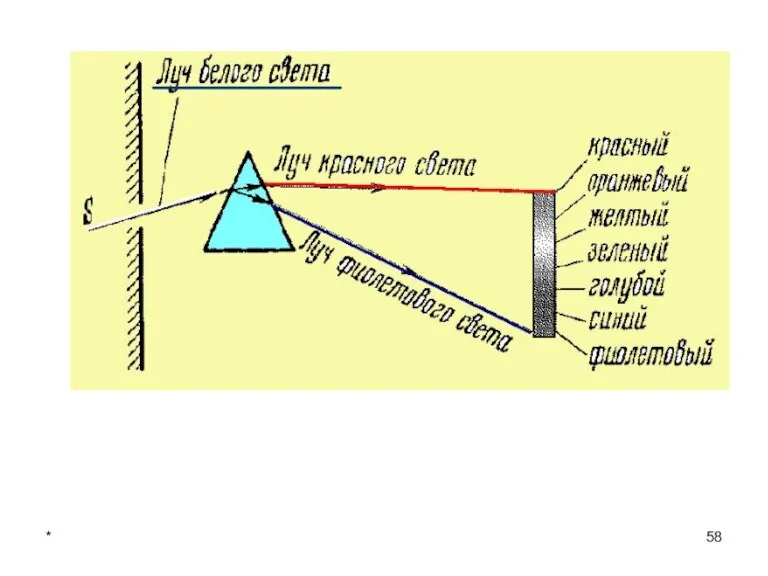
- 57. * Лекции проф. П.Ю.Гуляева Увеличением длины волны dn/dλ dn/dλ >0. Такая дисперсия называется аномальной. На явлении
- 58. * Лекции проф. П.Ю.Гуляева
- 59. * Лекции проф. П.Ю.Гуляева 26. Электронная теория дисперсии. Электронная теория дисперсии Лоренца рассматривает дисперсию света как
- 60. * Лекции проф. П.Ю.Гуляева В оптической области спектра частота колебаний электрического поля световой волны высока( ν≈1013
- 61. * Лекции проф. П.Ю.Гуляева Пусть внешнее поле E изменяется по гармоническому закону Е=E0Cos ωt . Тогда
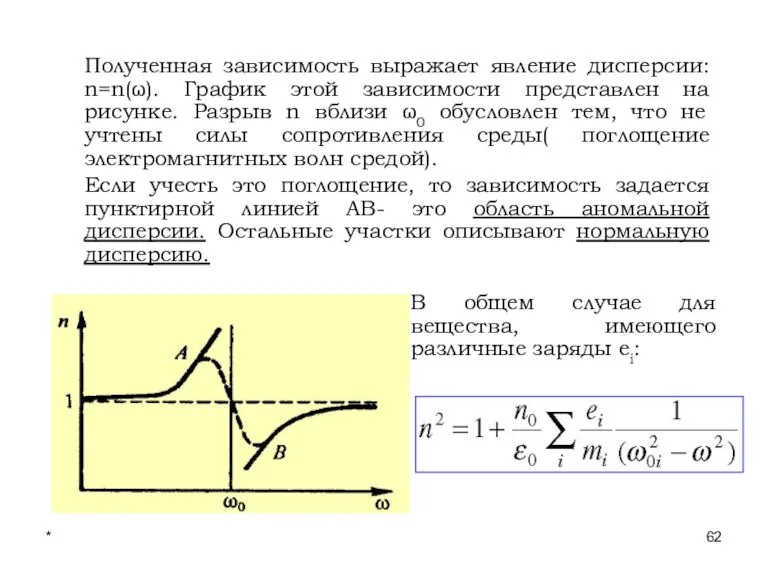
- 62. * Лекции проф. П.Ю.Гуляева Полученная зависимость выражает явление дисперсии: n=n(ω). График этой зависимости представлен на рисунке.
- 63. * Лекции проф. П.Ю.Гуляева 27. Поглощение( адсорбция) света. Поглощением( адсорбцией) света называется явление уменьшения энергии световой
- 64. * Лекции проф. П.Ю.Гуляева 28. Виды спектров поглощения. Линейчатый спектр поглощения- характерен для одноатомных газов( или
- 65. * Лекции проф. П.Ю.Гуляева Поляризация света 29. Естественный и поляризованный свет Для описания закономерностей поляризации будем
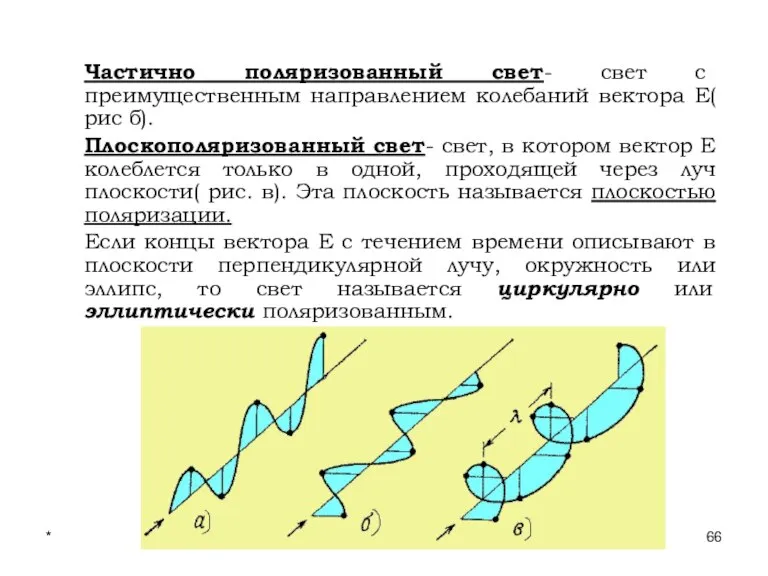
- 66. * Лекции проф. П.Ю.Гуляева Частично поляризованный свет- свет с преимущественным направлением колебаний вектора Е( рис б).
- 67. * Лекции проф. П.Ю.Гуляева Степенью поляризации называется величина: , где Imax и I min- соответственно максимальная
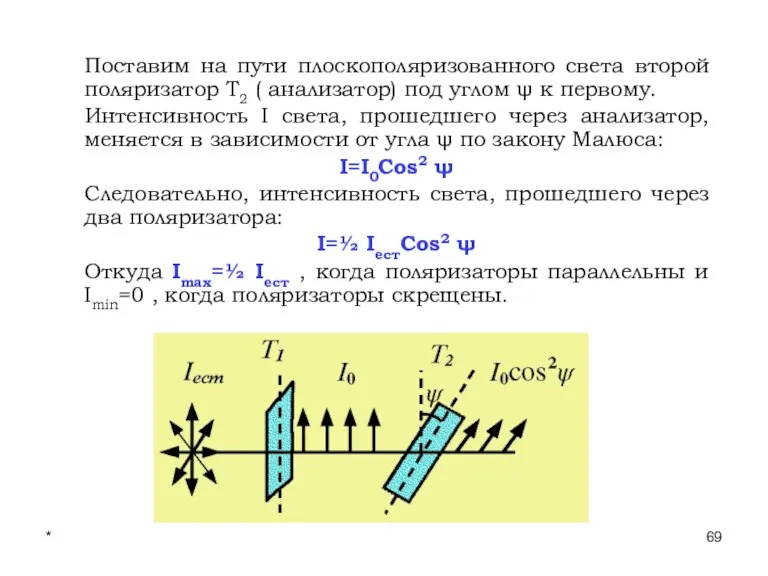
- 68. * Лекции проф. П.Ю.Гуляева 30. Закон Малюса Пропустим естественный свет с интенсивностью Iест через поляризатор Т1.
- 69. * Лекции проф. П.Ю.Гуляева Поставим на пути плоскополяризованного света второй поляризатор T2 ( анализатор) под углом
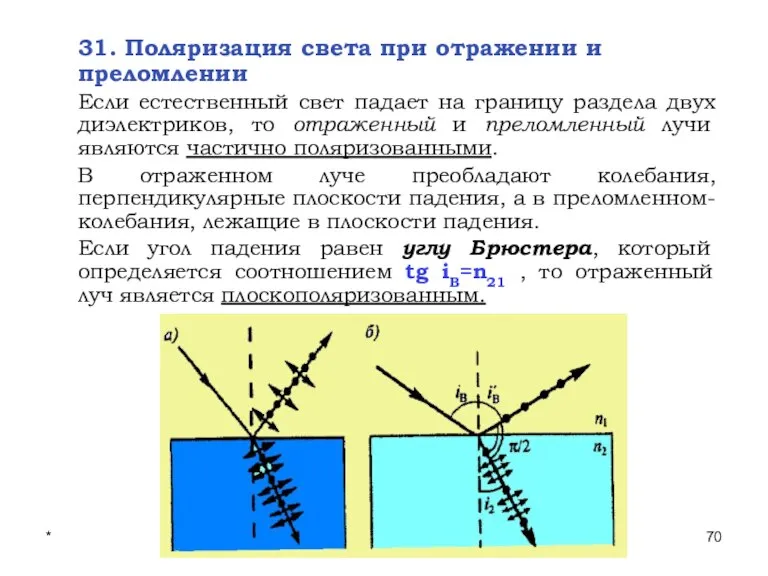
- 70. * Лекции проф. П.Ю.Гуляева 31. Поляризация света при отражении и преломлении Если естественный свет падает на
- 71. * Лекции проф. П.Ю.Гуляева Преломленный луч в этом случае поляризуется максимально, но не полностью. При этом
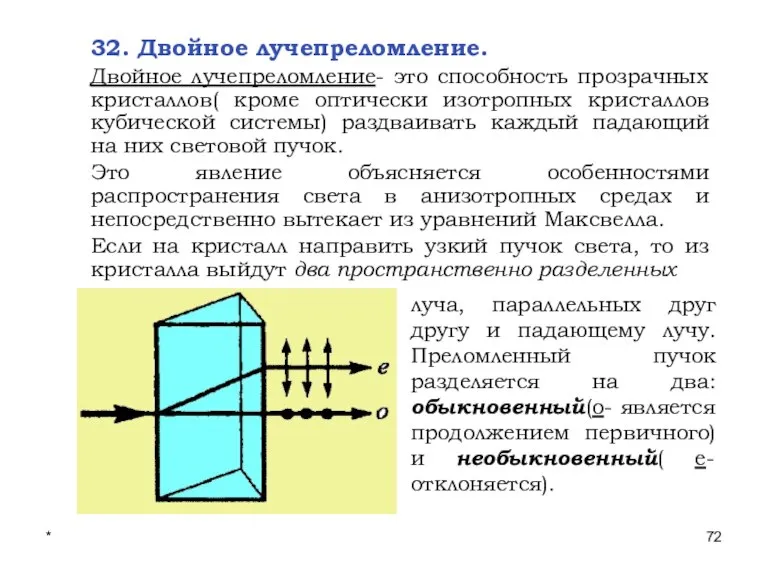
- 72. * Лекции проф. П.Ю.Гуляева 32. Двойное лучепреломление. Двойное лучепреломление- это способность прозрачных кристаллов( кроме оптически изотропных
- 73. * Лекции проф. П.Ю.Гуляева Направление в оптически анизотропном кристалле, по которому луч света распространяется, не испытывая
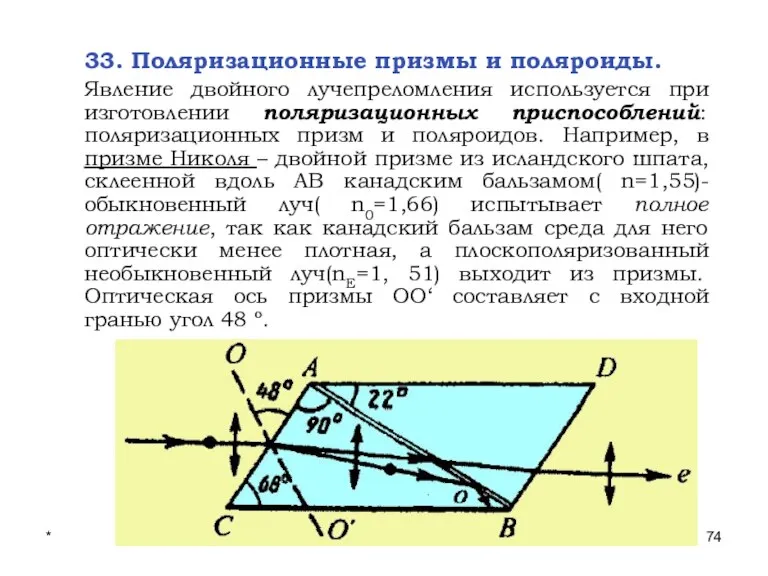
- 74. * Лекции проф. П.Ю.Гуляева 33. Поляризационные призмы и поляроиды. Явление двойного лучепреломления используется при изготовлении поляризационных
- 75. * Лекции проф. П.Ю.Гуляева Двоякопреломляющие кристаллы обладают свойством дихроизма- различного поглощения света в зависимости от ориентации
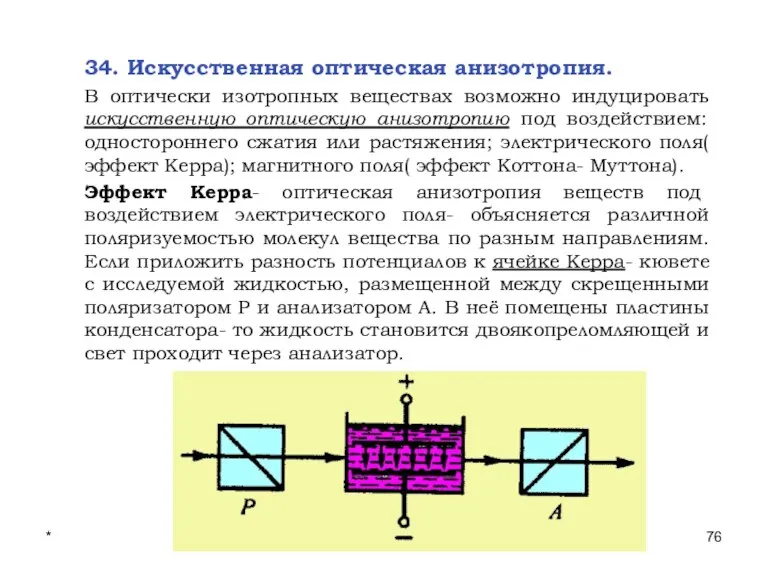
- 76. * Лекции проф. П.Ю.Гуляева 34. Искусственная оптическая анизотропия. В оптически изотропных веществах возможно индуцировать искусственную оптическую
- 77. * Лекции проф. П.Ю.Гуляева Разность показателей преломления обыкновенного и необыкновенного лучей:ne- n0=Bλ0E2 , где В- постоянная
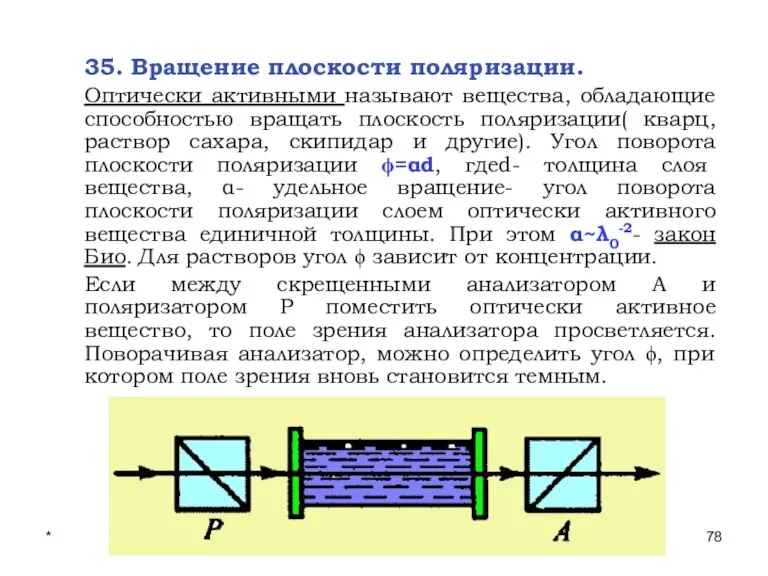
- 78. * Лекции проф. П.Ю.Гуляева 35. Вращение плоскости поляризации. Оптически активными называют вещества, обладающие способностью вращать плоскость
- 79. * Лекции проф. П.Ю.Гуляева В зависимости от направления вращения, оптически активные вещества разделяются на право- и
- 80. * Лекции проф. П.Ю.Гуляева Квантовая природа излучения Квантовая оптика- раздел оптики, занимающийся изучением явлений, в которых
- 81. * Лекции проф. П.Ю.Гуляева Равновесным состоянием системы тело- излучение является состояние, при котором распределение энергии между
- 82. * Лекции проф. П.Ю.Гуляева 37. Тепловое излучение и его характеристики. Тепловое излучение совершается за счет теплового
- 83. * Лекции проф. П.Ю.Гуляева Испускательную способность можно представить в виде функции длины волны, исходя из формулы
- 84. * Лекции проф. П.Ю.Гуляева 38. Абсолютно черное тело Тело, способное поглощать при любой температуре все падающее
- 85. * Лекции проф. П.Ю.Гуляева 39. Закон Кирхгофа. Закон Кирхгофа определяет соотношение между испускательной и поглощательной способностями
- 86. * Лекции проф. П.Ю.Гуляева 40.Закон Стефана- Больцмана Энергетическая светимость серого тела( интегральная по ν): Эту зависимость
- 87. * Лекции проф. П.Ю.Гуляева 41. Закон смещения Вина Положение минимума в спектре излучения черного тела описывается
- 88. * Лекции проф. П.Ю.Гуляева 42. Формулы Релея- Джинса и Вина Применяя к тепловому излучению классический закон
- 89. * Лекции проф. П.Ю.Гуляева Формула Релея- Джинса согласуется с экспериментом только в области малых частот и
- 90. * Лекции проф. П.Ю.Гуляева 43. Квантовая гипотеза Планка. Макс Планк предположил, что теория классического осциллятора неприменима
- 91. * Лекции проф. П.Ю.Гуляева Отсюда можно получить выражение для средней энергии осцилляторов: Тогда универсальная функция Кирхгофа
- 92. * Лекции проф. П.Ю.Гуляева В области малых частот hν Закон Стефана- Больцмана Re=σΤ4 получается из формулы
- 93. * Лекции проф. П.Ю.Гуляева 44. Фотоэффект. Фотоэлектрическим эффектом( фотоэффектом) называется высвобождение электронов под действием электромагнитного излучения.
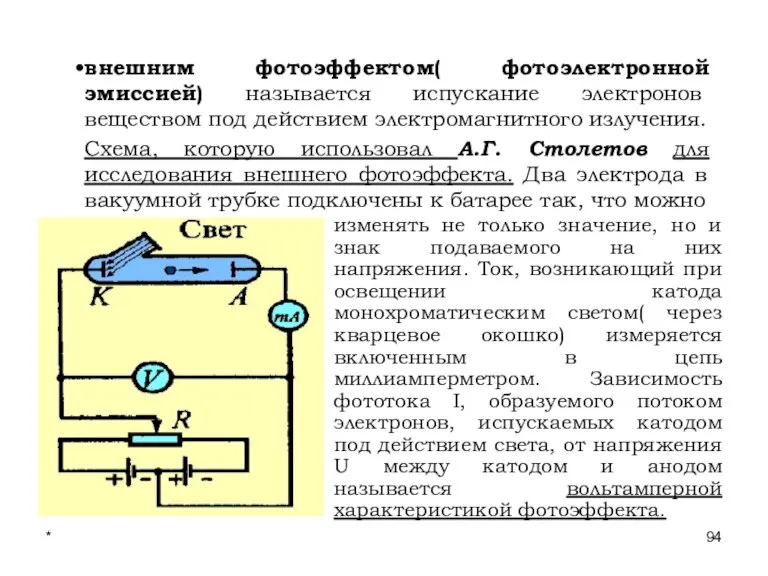
- 94. * Лекции проф. П.Ю.Гуляева внешним фотоэффектом( фотоэлектронной эмиссией) называется испускание электронов веществом под действием электромагнитного излучения.
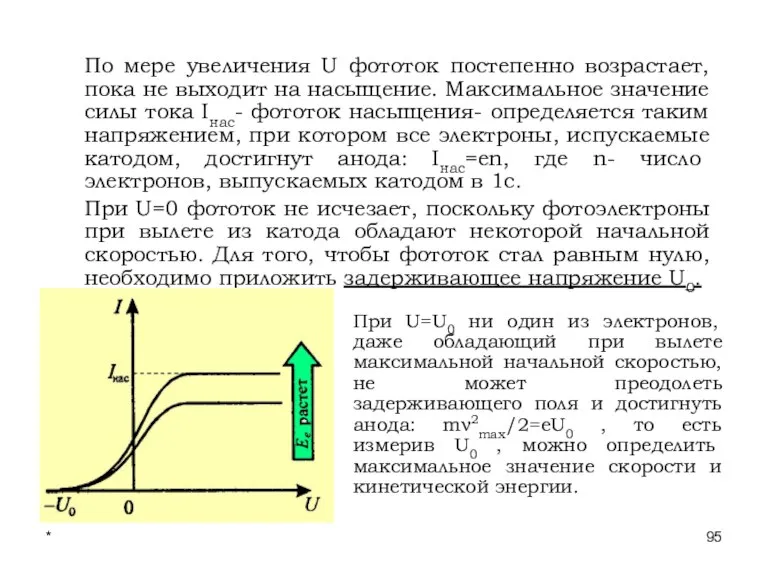
- 95. * Лекции проф. П.Ю.Гуляева По мере увеличения U фототок постепенно возрастает, пока не выходит на насыщение.
- 96. * Лекции проф. П.Ю.Гуляева 45. Законы фотоэффекта. Закон Столетова: при фиксированной частоте падающего света число фотоэлектронов,
- 97. * Лекции проф. П.Ю.Гуляева Для объяснения механизма фотоэффекта А.Эйнштейн предположил, что свет частотой ν не только
- 98. * Лекции проф. П.Ю.Гуляева 46. Масса и импульс фотона. Единство корпускулярных и волновых свойств света. Энергия
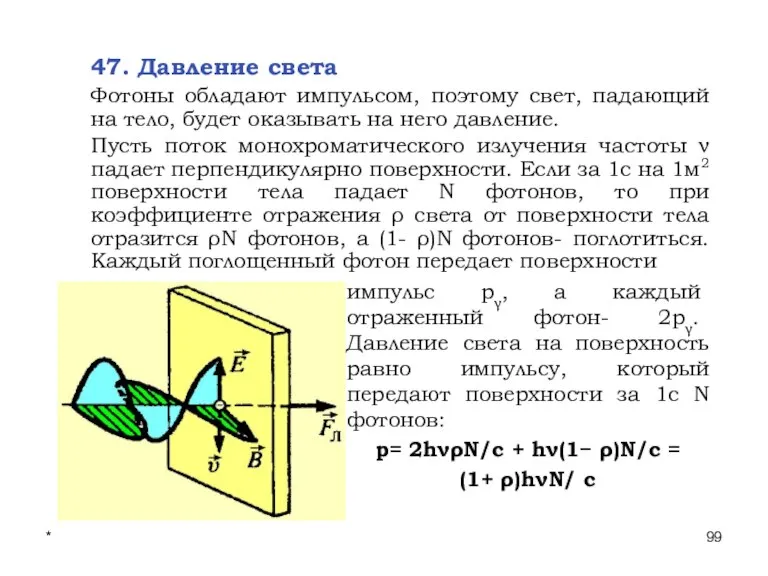
- 99. * Лекции проф. П.Ю.Гуляева 47. Давление света Фотоны обладают импульсом, поэтому свет, падающий на тело, будет
- 100. * Лекции проф. П.Ю.Гуляева hνΝ= Ee – энергия всех фотонов, падающих на единицу поверхности в единицу
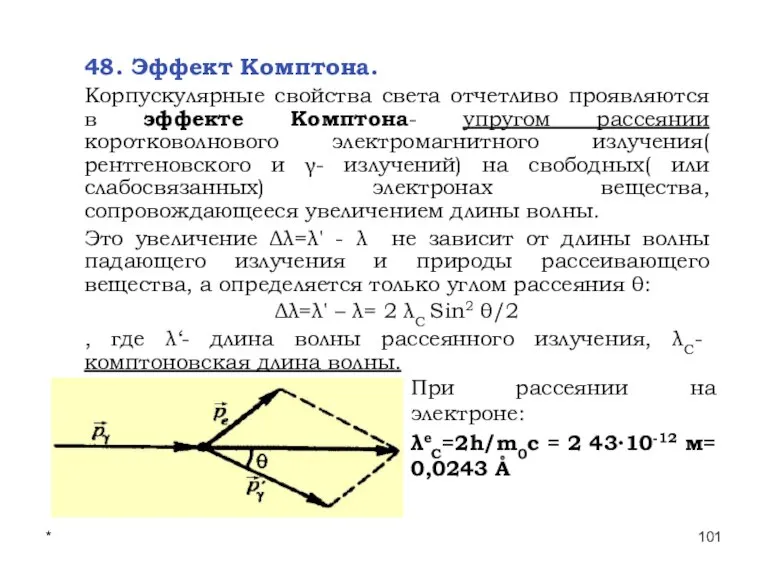
- 101. * Лекции проф. П.Ю.Гуляева 48. Эффект Комптона. Корпускулярные свойства света отчетливо проявляются в эффекте Комптона- упругом
- 102. * Лекции проф. П.Ю.Гуляева Фотон( с энергией εγ= hν и импульсом εγ= hν и импульсом рγ=
- 104. Скачать презентацию





























































 Влияние дефектов на физические свойства кристаллов
Влияние дефектов на физические свойства кристаллов Скорость. Расчет пути и времени движения
Скорость. Расчет пути и времени движения Механика деформируемого твердого тела
Механика деформируемого твердого тела Дифракция
Дифракция Noteikt daļiņas lādiņa zīmi pēc kreisas rokas likuma!
Noteikt daļiņas lādiņa zīmi pēc kreisas rokas likuma! Теоретические основы электротехники. Теория электромагнитного поля. Лекция 10
Теоретические основы электротехники. Теория электромагнитного поля. Лекция 10 Юные физики. Игра. 7 класс
Юные физики. Игра. 7 класс Паросиловая установка (ПСУ)
Паросиловая установка (ПСУ) Импульс тела. Закон сохранения импульса
Импульс тела. Закон сохранения импульса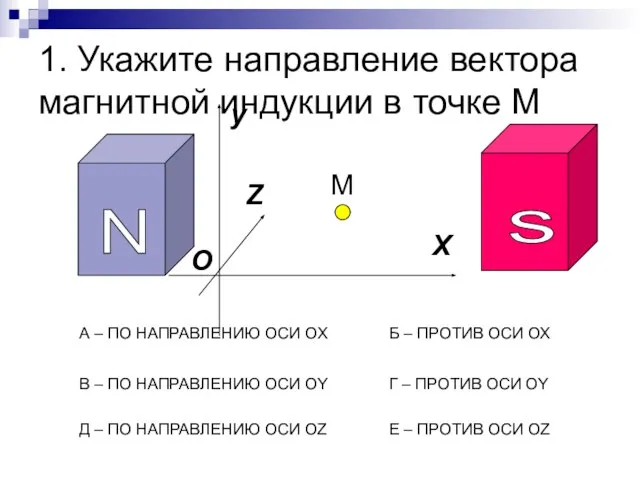 Тест по теме Электромагнетизм
Тест по теме Электромагнетизм Цепи с сопротивлением, индуктивностью, ёмкостью
Цепи с сопротивлением, индуктивностью, ёмкостью Механика. Комплексный экзамен
Механика. Комплексный экзамен Зубчатые передачи
Зубчатые передачи 1426584
1426584 Презентация на тему Низкочастотные колебания
Презентация на тему Низкочастотные колебания  Валерий Брюсов “Мир электрона”. (1922г)
Валерий Брюсов “Мир электрона”. (1922г) Первый закон термодинамики
Первый закон термодинамики Преломление света. Физический смысл показателя преломления. Электромагнитные явления
Преломление света. Физический смысл показателя преломления. Электромагнитные явления Физика атомного ядра и элементарных частиц
Физика атомного ядра и элементарных частиц Cокол тысячелетия 10,08
Cокол тысячелетия 10,08 И. Кеплер, и его вклад и развитие механики
И. Кеплер, и его вклад и развитие механики Рентгеновские лучи
Рентгеновские лучи Система пуска двигателя
Система пуска двигателя Взаимодействие тел
Взаимодействие тел Введение в предмет Микросхемотехника
Введение в предмет Микросхемотехника Освещение. Свет и тень
Освещение. Свет и тень Основы строительных конструкций. Метод предельного равновесия. Лекция 10
Основы строительных конструкций. Метод предельного равновесия. Лекция 10 Ефективність грохочення
Ефективність грохочення