Слайд 2Задание 1. Вычислить определенный интеграл по формуле Ньютона-Лейбница.

Слайд 3Задание 2. Вычислить определенный интеграл методом замены переменной интегрирования.

Слайд 5Вычисление площади криволинейной трапеции
Если - непрерывная функция, на [a, b], то
![Вычисление площади криволинейной трапеции Если - непрерывная функция, на [a, b], то](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1149953/slide-4.jpg)
Слайд 6Вычисление площади криволинейной трапеции
Если - непрерывная функция, на [a, b], то
![Вычисление площади криволинейной трапеции Если - непрерывная функция, на [a, b], то](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1149953/slide-5.jpg)
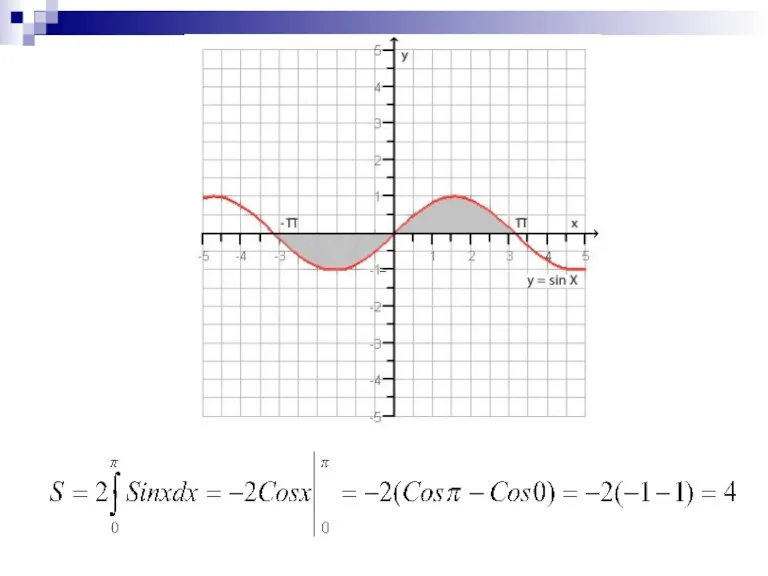
Слайд 7Вычисление площади криволинейной трапеции
Если непрерывная на [a; c], непрерывная на [c; b]
где
![Вычисление площади криволинейной трапеции Если непрерывная на [a; c], непрерывная на [c; b] где , то](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1149953/slide-6.jpg)
, то
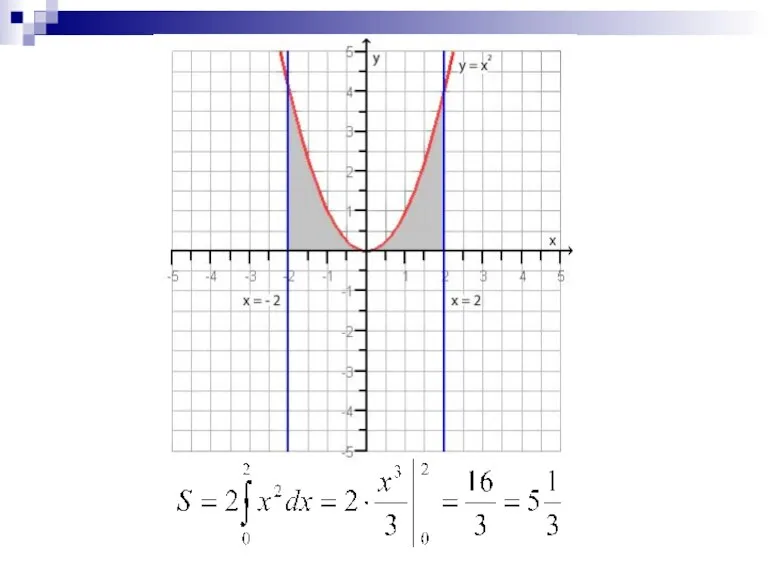
Слайд 8Пример №1: Найти площадь фигуры, ограниченной параболой y=x2, прямыми x=1, x=3 и
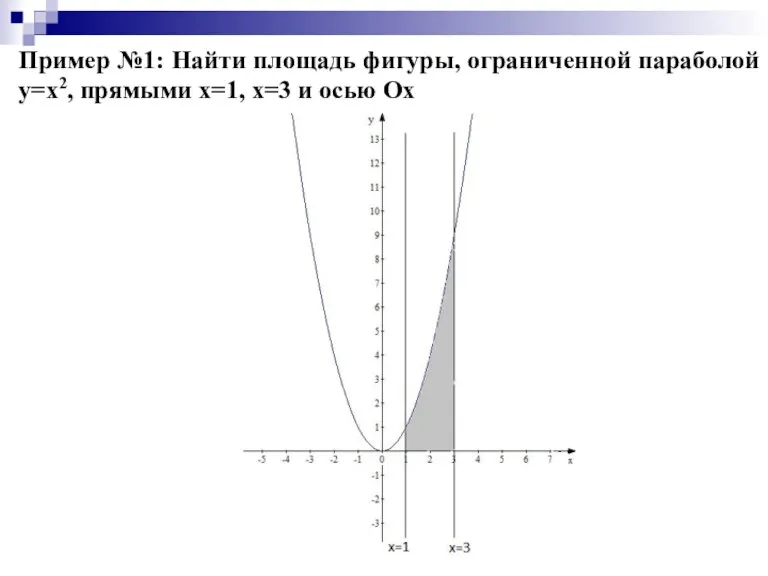
осью Ох
Слайд 9Вычисление площадей плоских фигур
Если - непрерывные функции на [a; b],
на
![Вычисление площадей плоских фигур Если - непрерывные функции на [a; b], на [a; b], то](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1149953/slide-8.jpg)
[a; b], то
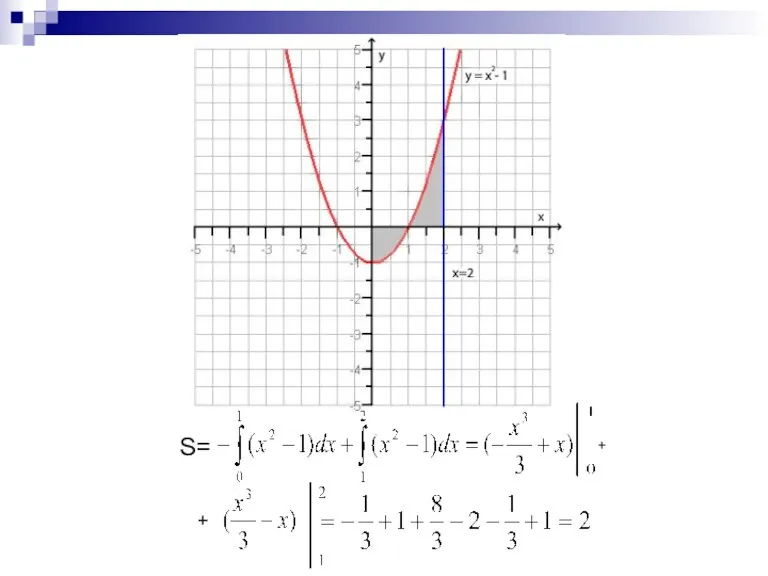
Слайд 10Вычисление площадей плоских фигур
Если y=f(x), y= g(x) непрерывные функции на [а; в],
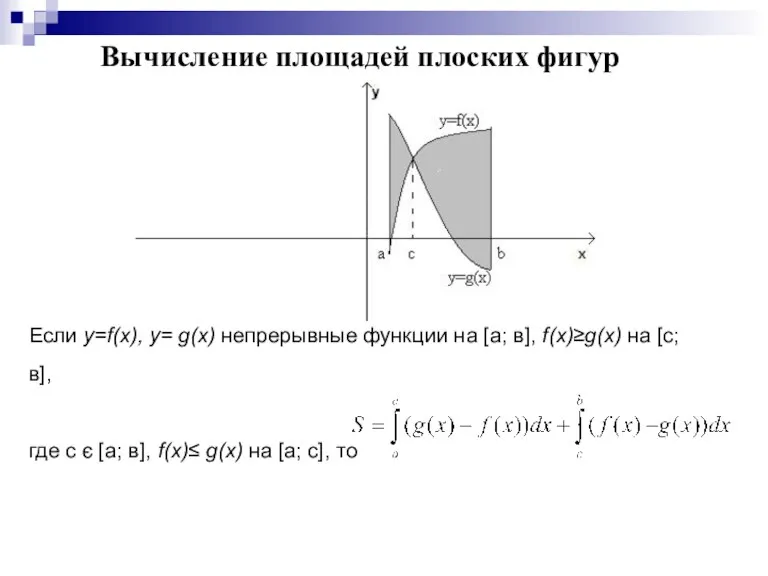
f(x)≥g(x) на [с; в],
где с є [а; в], f(x)≤ g(x) на [а; с], то
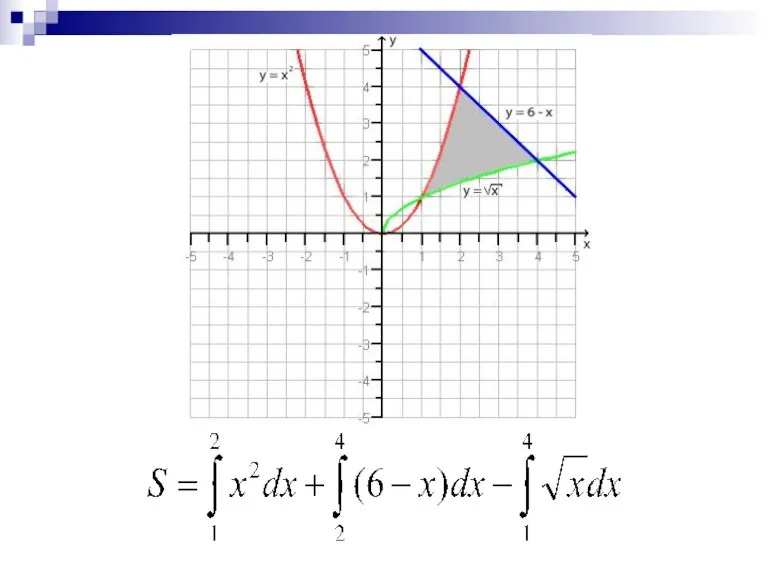
Слайд 11Вычислить площадь фигуры, ограниченной линиями у=х+3, у=х2 +1
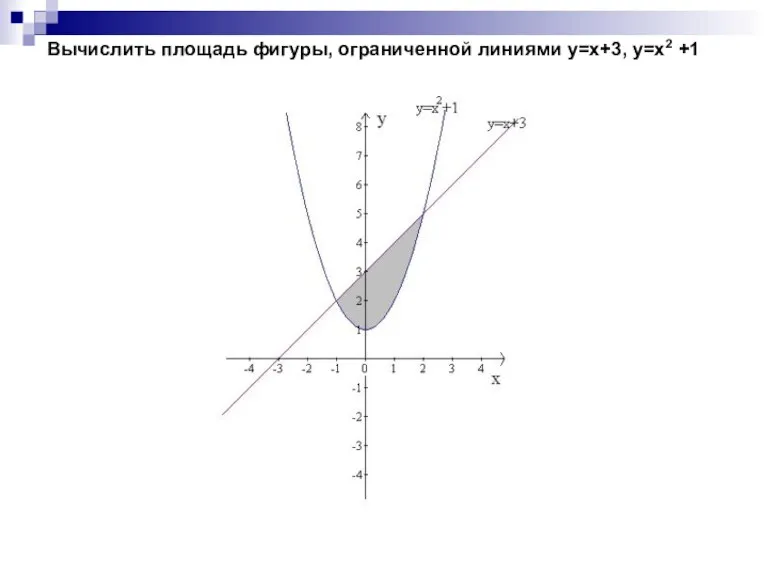
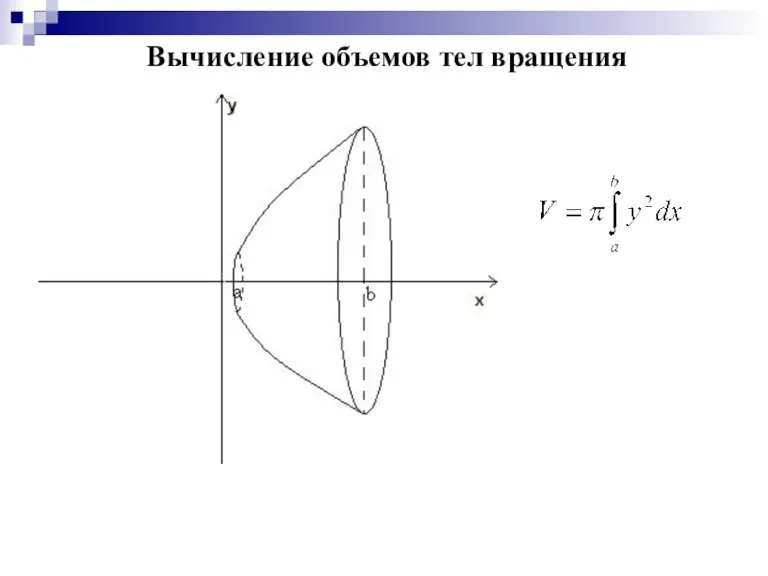
Слайд 13Найти объем тела, образованного вращением вокруг оси Ох плоской фигуры, ограниченной линиями
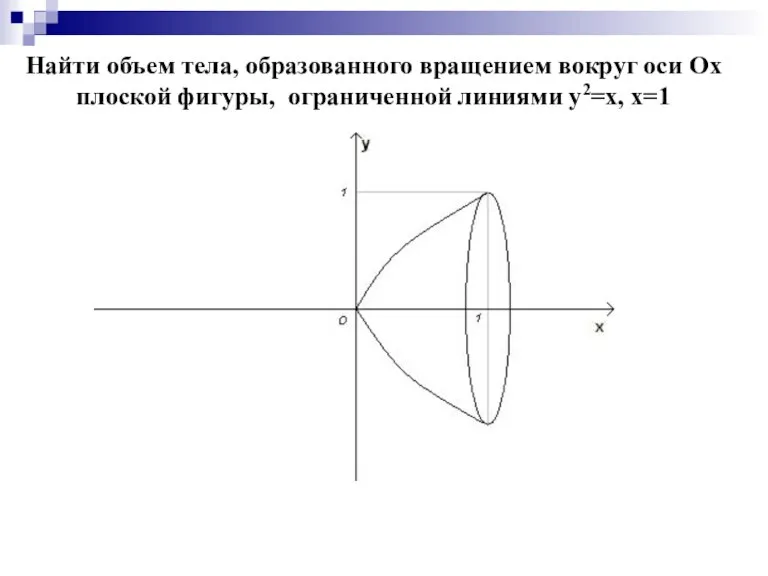
у2=х, х=1



![Вычисление площади криволинейной трапеции Если - непрерывная функция, на [a, b], то](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1149953/slide-4.jpg)
![Вычисление площади криволинейной трапеции Если - непрерывная функция, на [a, b], то](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1149953/slide-5.jpg)
![Вычисление площади криволинейной трапеции Если непрерывная на [a; c], непрерывная на [c; b] где , то](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1149953/slide-6.jpg)

![Вычисление площадей плоских фигур Если - непрерывные функции на [a; b], на [a; b], то](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1149953/slide-8.jpg)



 Сложение чисел с разными знаками
Сложение чисел с разными знаками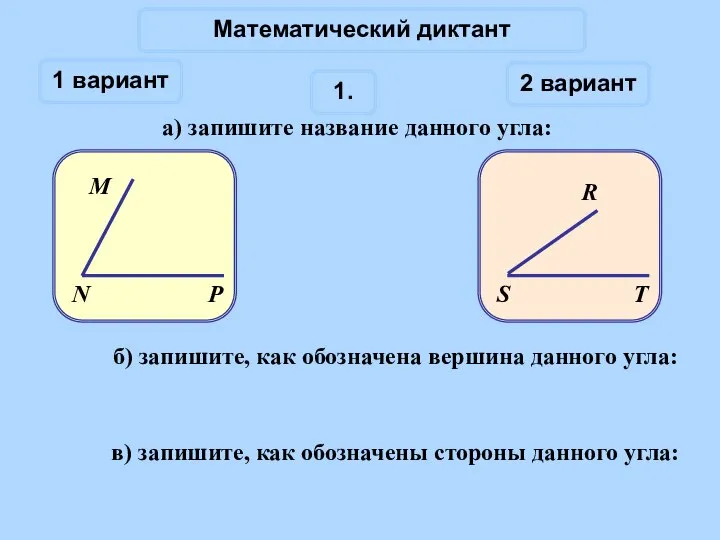 Углы. Математический диктант
Углы. Математический диктант Интеграл. Что называют криволинейной
Интеграл. Что называют криволинейной Применение игровых технологий на уроках математики в условиях внедрения ФГОС
Применение игровых технологий на уроках математики в условиях внедрения ФГОС Применение параллелограмма
Применение параллелограмма Прямоугольник. Геометрия, 8класс
Прямоугольник. Геометрия, 8класс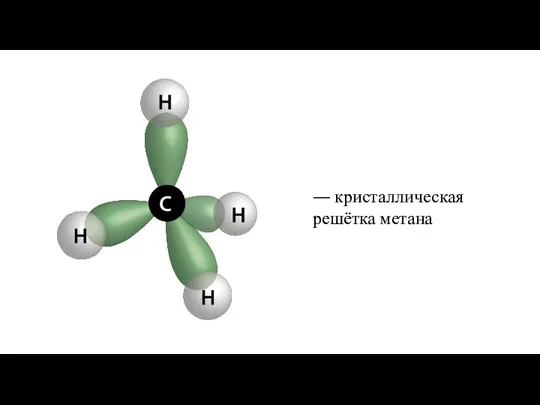 12. Тэтраэдр
12. Тэтраэдр Решение систем уравнений второй степени различными способами
Решение систем уравнений второй степени различными способами Решение примеров и задач с числами, полученными при измерении стоимости
Решение примеров и задач с числами, полученными при измерении стоимости Презентация на тему Симметрия и движение (9 класс)
Презентация на тему Симметрия и движение (9 класс)  Типы алгоритмов
Типы алгоритмов Современная финансовая математика
Современная финансовая математика Объем пирамиды
Объем пирамиды Применение осевой симметрии в жизни
Применение осевой симметрии в жизни Проценты. ОГЭ и ЕГЭ
Проценты. ОГЭ и ЕГЭ Непрерывность функций
Непрерывность функций Пересечение линии и поверхности. Позиционные задачи. (Лекция 8.2)
Пересечение линии и поверхности. Позиционные задачи. (Лекция 8.2) Решаем задачу
Решаем задачу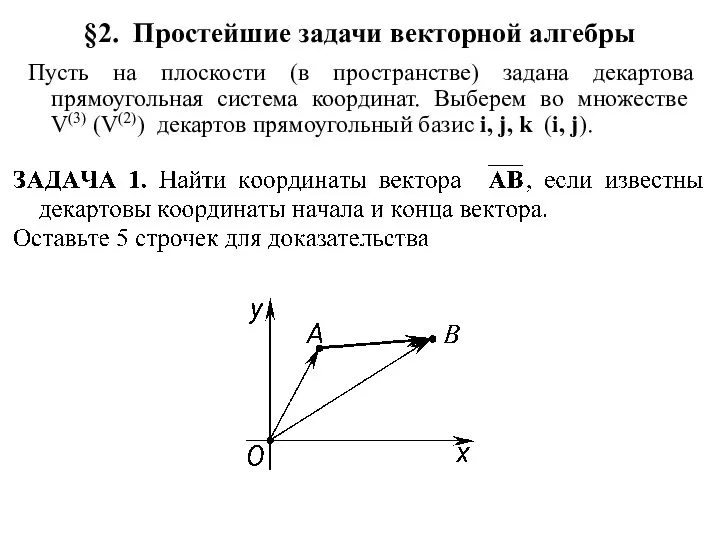 Простейшие задачи векторной алгебры
Простейшие задачи векторной алгебры Элементы теории фредгольмовых отображений
Элементы теории фредгольмовых отображений Статистическая проверка статистических гипотез
Статистическая проверка статистических гипотез Числовая окружность
Числовая окружность Соотношения между сторонами и углами треугольника. Подготовка к контрольной работе
Соотношения между сторонами и углами треугольника. Подготовка к контрольной работе Задачи на расстояния в пространстве
Задачи на расстояния в пространстве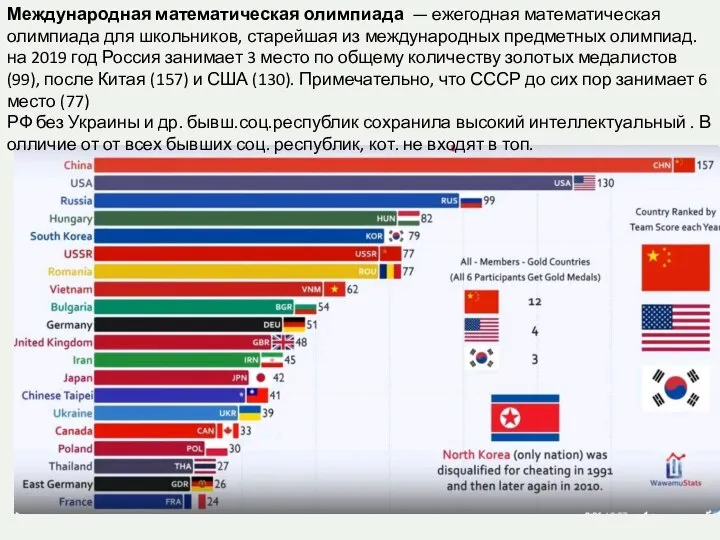 Международная математическая олимпиада
Международная математическая олимпиада Планиметрия. От углов до многоугольников. Повторение материала
Планиметрия. От углов до многоугольников. Повторение материала Увеличение и уменьшение на несколько %
Увеличение и уменьшение на несколько % Степенные функции
Степенные функции