Содержание
- 2. Тематика лекционных занятий: Основы гидравлики Общие сведения об объемных гидроприводах Объемные гидромашины Гидроаппараты Кондиционеры рабочей жидкости,
- 3. 1.6 Уравнение Бернулли Основным уравнением гидродинамики является уравнение Бернулли, которое устанавливает связь между скоростью движения и
- 4. Уравнение Бернулли
- 5. Уравнение Бернулли для потока реальной жидкости Поправки: Средняя скорость потока, а не постоянная скорость струйки. Уравнение
- 6. 1.7 Режимы течения жидкости При ламинарном режиме течения частицы жидкости перемещаются по траекториям, направленным вдоль потока
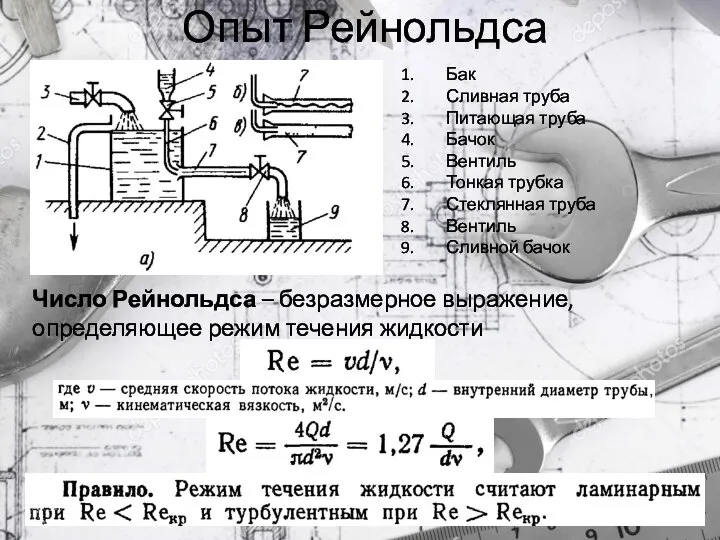
- 7. Опыт Рейнольдса Бак Сливная труба Питающая труба Бачок Вентиль Тонкая трубка Стеклянная труба Вентиль Сливной бачок
- 8. Практическое определение числа Рейнольдса Если расход Q задан в л/мин, d – в мм, ν –
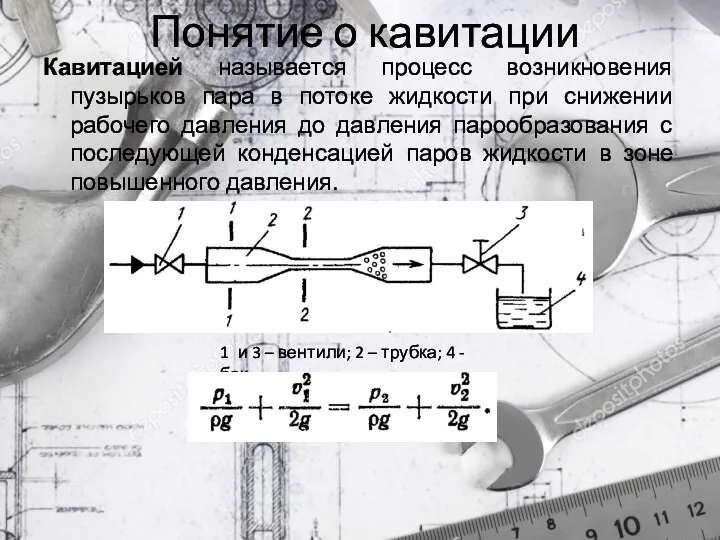
- 9. Понятие о кавитации Кавитацией называется процесс возникновения пузырьков пара в потоке жидкости при снижении рабочего давления
- 10. 1.8 Расчет простых трубопроводов. Потери давления в трубопроводах Простым называют трубопровод, не имеющий боковых ответвлений. Цель
- 11. Пример Определить условный проход напорного трубопровода, если расход Q = 45 л/мин и номинальное давление pном
- 12. Потери давления в трубопроводах по длине Различают два вида потерь: потери по длине hl и местные
- 13. Коэффициент Дарси для ламинарного и турбулентного потока На практике применяют выражение:
- 14. Пример Гладкий круглый трубопровод с внутренним диаметром d = 10 мм имеет длину l = 2
- 15. Эмпирические формулы потерь давления по длине ламинарный режим: турбулентный режим:
- 16. Местные потери давления в трубопроводах Местные потери напора: ζ (дзета) – как правило определяют экспериментальным путём
- 17. Пример Рабочая жидкость - минеральное масло перемещается по трубопроводу диаметром 10 мм через местное сопротивление, коэффициент
- 18. Понятие об эквивалентной длине Длиной, эквивалентной длине данного местного сопротивления, считается такая длина прямой трубы, на
- 19. Расчет труб на прочность Тонкостенные трубы - или Толщина стенки трубы: Допускаемое напряжение:
- 21. Скачать презентацию
















 Метрология. Случайные погрешности: статистические методы оценивания
Метрология. Случайные погрешности: статистические методы оценивания Единицы работы электрического тока, применяемые на практике
Единицы работы электрического тока, применяемые на практике Оптические явления
Оптические явления МБОУ «Юхмачинская средняя общеобразовательная школа» Алькеевского муниципального района Республики Татарстан ФИЗИКА В ПРИРОДЕ
МБОУ «Юхмачинская средняя общеобразовательная школа» Алькеевского муниципального района Республики Татарстан ФИЗИКА В ПРИРОДЕ  Презентация на тему Электрическая цепь
Презентация на тему Электрическая цепь  Адиабатическое приближение
Адиабатическое приближение Лётные и эксплуатационные ограничения многодвигательного ВС DA-42. Тема 7
Лётные и эксплуатационные ограничения многодвигательного ВС DA-42. Тема 7 Физика. Физические явления
Физика. Физические явления Динер Никита Физика Инерция
Динер Никита Физика Инерция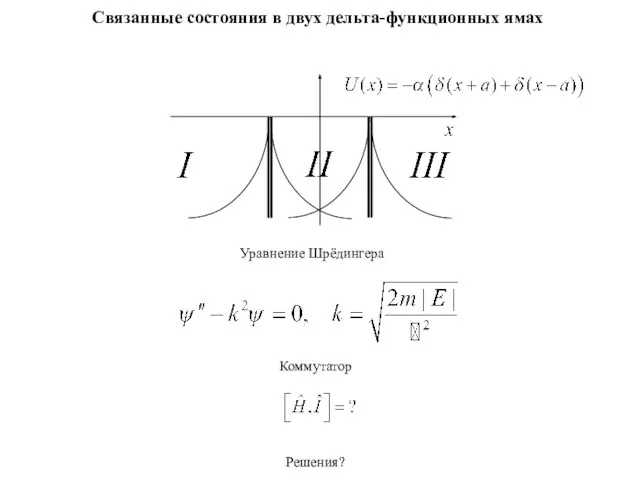 Связанные состояния в двух дельта - функционных ямах
Связанные состояния в двух дельта - функционных ямах Солнце, воздух и вода – наши лучшие друзья
Солнце, воздух и вода – наши лучшие друзья Револьверный станок
Револьверный станок Магнитное поле
Магнитное поле Внутренняя энергия. Работа в термодинамике. Количество теплоты
Внутренняя энергия. Работа в термодинамике. Количество теплоты Иллюзии и Физика. Вечная Борьба
Иллюзии и Физика. Вечная Борьба Теория пластин
Теория пластин Расчёт кругового поворота автомобиля
Расчёт кругового поворота автомобиля Сила трения
Сила трения Презентация на тему Кипение
Презентация на тему Кипение  Интерактивные лабораторные работы по физике
Интерактивные лабораторные работы по физике Нанотехнологии вокруг нас
Нанотехнологии вокруг нас Презентация на тему Сложение сил, направленных вдоль одной прямой. Равнодействующая сила
Презентация на тему Сложение сил, направленных вдоль одной прямой. Равнодействующая сила  Физика и В.О.В
Физика и В.О.В Способы увеличения подачи воздуха и топлива в цилиндры двигателя внутреннего сгорания (ДВС)
Способы увеличения подачи воздуха и топлива в цилиндры двигателя внутреннего сгорания (ДВС)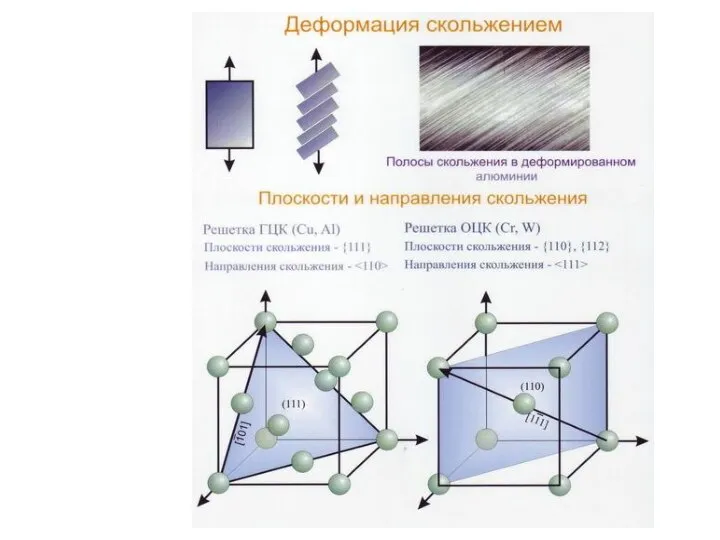 Пластическая деформация металлов
Пластическая деформация металлов ИК-спектроскопия
ИК-спектроскопия Техобслуживание
Техобслуживание Термодинамические системы и термодинамические параметры
Термодинамические системы и термодинамические параметры