Слайд 2Проекцией вектора на плоскость называется вектор, заключённый между проекциями начала и конца
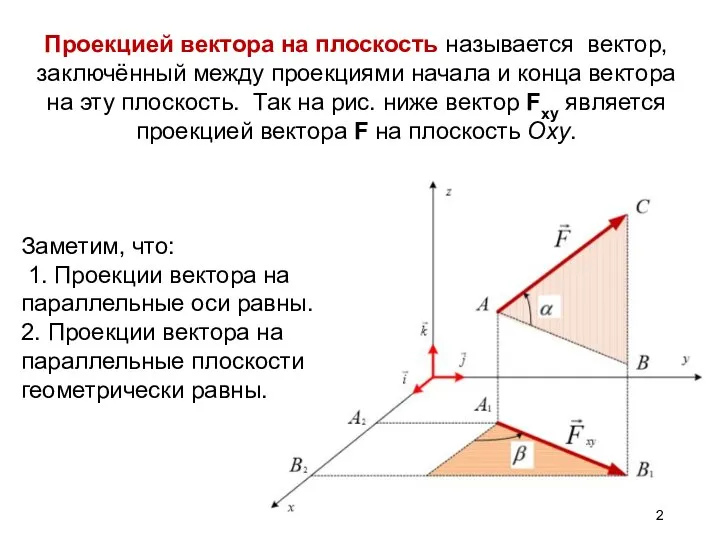
вектора на эту плоскость. Так на рис. ниже вектор Fxy является проекцией вектора F на плоскость Oxy.
Заметим, что:
1. Проекции вектора на
параллельные оси равны.
2. Проекции вектора на
параллельные плоскости
геометрически равны.
Слайд 3Вектор может быть представлен в виде суммы трёх векторов, каждый из которых
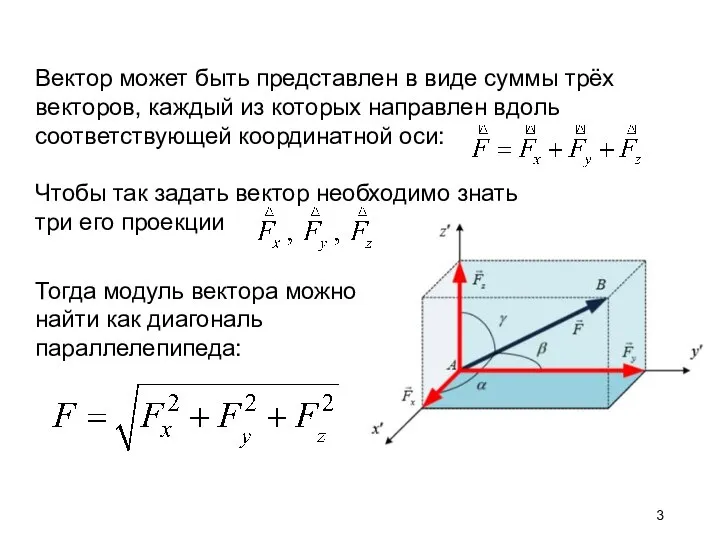
направлен вдоль соответствующей координатной оси:
Чтобы так задать вектор необходимо знать
три его проекции
Тогда модуль вектора можно
найти как диагональ
параллелепипеда:
Слайд 4Графический способ сложения сил заключается в построении параллелограмма сил.
Вектор, равный векторной

(геометрической) сумме всех сил, действующих в системе будем называть
главным вектором системы сил.
Главный вектор не зависит от порядка суммирования векторов.



 Напряжённость электрического поля
Напряжённость электрического поля Результаты экспериментальных исследований теплофизических характеристик автоклавного ячеистого бетона
Результаты экспериментальных исследований теплофизических характеристик автоклавного ячеистого бетона Свойства звуковых волн
Свойства звуковых волн Электрическая система. Процесс
Электрическая система. Процесс Графики в задачах по кинематике
Графики в задачах по кинематике Атомная и ядерная физика
Атомная и ядерная физика Вклад советских учёных-физиков в Великую Победу
Вклад советских учёных-физиков в Великую Победу Действие магнитного поля на проводник с током. Сила ампера. Сила лоренца
Действие магнитного поля на проводник с током. Сила ампера. Сила лоренца Измеряем площадь взвешиванием
Измеряем площадь взвешиванием Колебания. Малые гармонические колебания
Колебания. Малые гармонические колебания Коррекция систем
Коррекция систем Общее устройство автомобиля
Общее устройство автомобиля Резонансы в электрических цепях
Резонансы в электрических цепях Потенциальная энергия. (Лекция 4)
Потенциальная энергия. (Лекция 4) Влияние электромагнитного излучения на организм и здоровье человека
Влияние электромагнитного излучения на организм и здоровье человека Нейтронное излучение: опасности и перспективы
Нейтронное излучение: опасности и перспективы Лекция 3
Лекция 3 Extended Defects in c-Si
Extended Defects in c-Si Решение задач на закон Ома
Решение задач на закон Ома Электрические силы
Электрические силы Внутреннее устройство фотоаппарата
Внутреннее устройство фотоаппарата Общая физика
Общая физика Электронный нос или что может заменить нос собаки
Электронный нос или что может заменить нос собаки Клей. История клея
Клей. История клея Подвеска автомобиля
Подвеска автомобиля Материалы, применяемые в электронике, электротехнике и радиотехнике
Материалы, применяемые в электронике, электротехнике и радиотехнике Основные понятия, определения и аксиомы механики
Основные понятия, определения и аксиомы механики Виды излучений
Виды излучений