Содержание
- 2. Что значит «прямолинейное»? Какое движение называется равноускоренным?
- 3. Формулы проекции перемещения координаты тела
- 4. Что означает х0? (начальная координата тела) Что означает V0x? (проекция начальной скорости) Что означает ах? (проекция
- 5. x = 15 – 4t – 2t2 x = 7,5 – 8t +16t2 х0 = 15
- 6. x = -11 + 3t+9t2 х0 = -11 V0x = 3 x = -20 + 5t
- 7. x ax 2 Назовите независимую переменную t = x0 + V0x t + t (аргумент) )
- 8. Назовите независимую переменную (аргумент) у ( х ) = а х + b х + с
- 9. Что является графиком этой функции? Как влияет знак перед старшим коэффициентом на направление ветвей? Этапы построения
- 10. с x0 b V0x a ax/2 2 у(х) = ах2 + bx + c
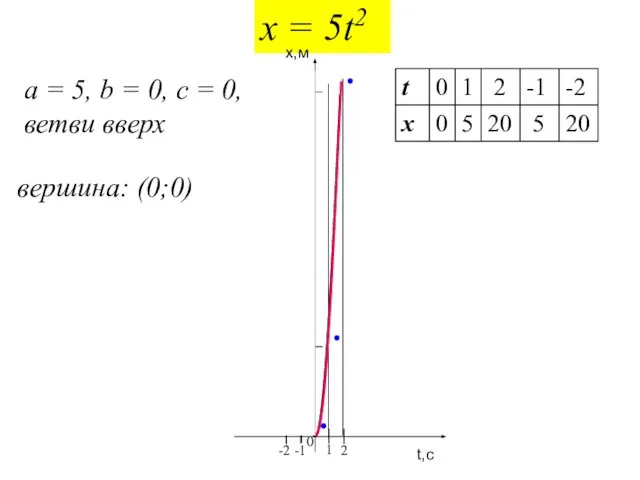
- 11. Задача №1. Построить график координаты от времени свободного падения тела от начального уровня. x0=0 V0x =
- 12. x = 5t2 a = 5, b = 0, c = 0, ветви вверх вершина: (0;0)
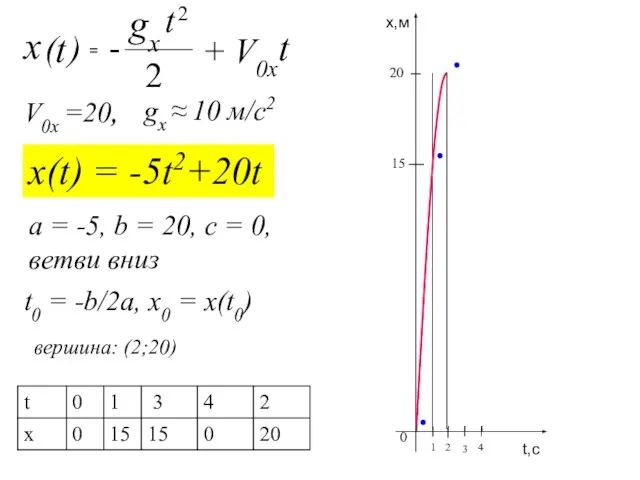
- 13. Задача №2. Построить график функции свободного падения шарика, брошенного вверх от нулевого уровня, со скоростью 20
- 14. x(t) = -5t2+20t V0x =20, gx ≈ 10 м/с2 вершина: (2;20) a = -5, b =
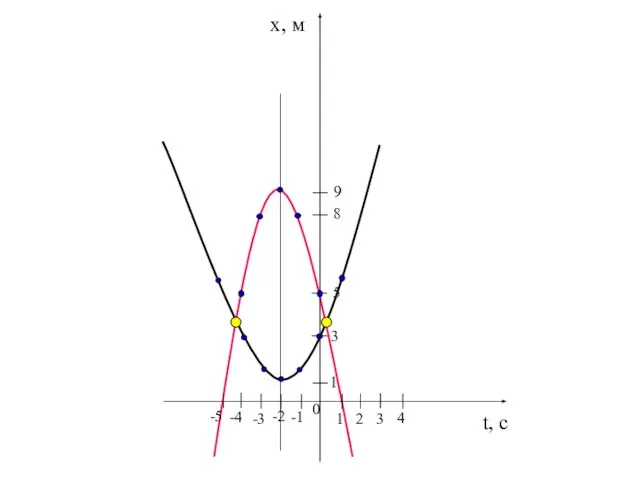
- 15. Задача №3. Движения 2-х тел заданы уравнениями х1 = 0,5t2 + 2t +3, x2 = -t2
- 16. х1 = 0,5t2 + 2t +3 вершина: t0 = -2/2⋅0,5 = -2 x0 = 0,5⋅4 -
- 17. t, c x, м 4 3 2 -4 -3 -2 -1 0 1 8 5 3
- 18. Точки пересечения: (0,3; 3,71) (-4,3; 3,71) Ответ: (0,3; 3,71).
- 19. Задача №4. Движения 2-х мотоциклистов заданы уравнениями: х1 = 9 + t2, х2 = 6t. 1.Охарактеризуйте
- 21. Скачать презентацию




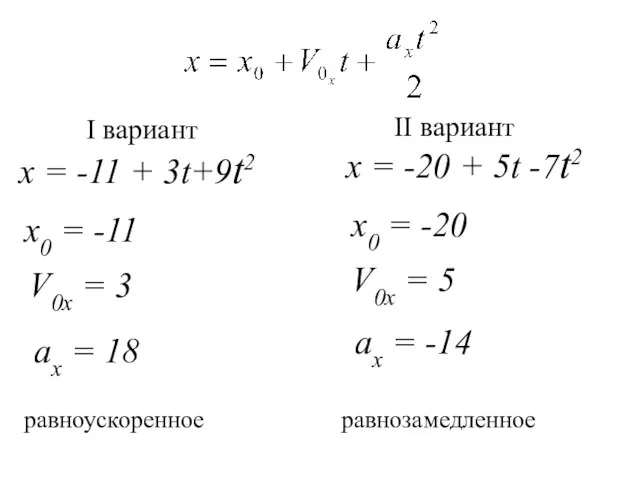



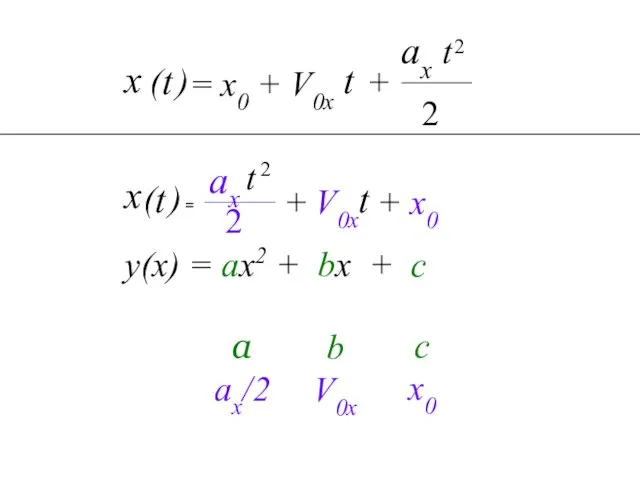






 Презентация на тему Корпускулярно-волновой дуализм
Презентация на тему Корпускулярно-волновой дуализм  Короткое замыкание. Предохранители
Короткое замыкание. Предохранители Развитие представлений о строении атома. Модель резерфорда
Развитие представлений о строении атома. Модель резерфорда СКОРОСТЬ СВЕТА
СКОРОСТЬ СВЕТА Математичне моделювання електричних кіл. Обчислення резистивних схем за матричним описання електротехнічної схеми
Математичне моделювання електричних кіл. Обчислення резистивних схем за матричним описання електротехнічної схеми Сверхпроводниковые материалы
Сверхпроводниковые материалы Биология. Физика. Химия. Радиация. Естествознание, 10 класс
Биология. Физика. Химия. Радиация. Естествознание, 10 класс Интерференция света
Интерференция света Звуковые волны
Звуковые волны Механические колебания. Тест
Механические колебания. Тест Классификация электротехнических материалов
Классификация электротехнических материалов Условия плавания тел
Условия плавания тел Презентация на тему Механическая работа и мощность (10 класс)
Презентация на тему Механическая работа и мощность (10 класс)  Равномерное движение (1)
Равномерное движение (1) Магнитное взаимодействие
Магнитное взаимодействие Линзы. Построения в линзах. 11 класс
Линзы. Построения в линзах. 11 класс Общие сведения о системах первичного электроснабжения РЭС
Общие сведения о системах первичного электроснабжения РЭС Градиент и его свойства
Градиент и его свойства Вес тела
Вес тела Влияние электромагнитного излучения на организм и здоровье человека
Влияние электромагнитного излучения на организм и здоровье человека Эффекты квантования чисел в цифровых цепях
Эффекты квантования чисел в цифровых цепях Физика в белом халате
Физика в белом халате Механика. Лекция 2
Механика. Лекция 2 Переходные процессы
Переходные процессы Електризація тіл. Види електризації
Електризація тіл. Види електризації Аппараты для исследования дальнего космоса. Тема № 3
Аппараты для исследования дальнего космоса. Тема № 3 Шпоночные соединёния
Шпоночные соединёния План структурной оптимизации технологического процесса изготовления кузова модели SX11
План структурной оптимизации технологического процесса изготовления кузова модели SX11