Идеальный газ

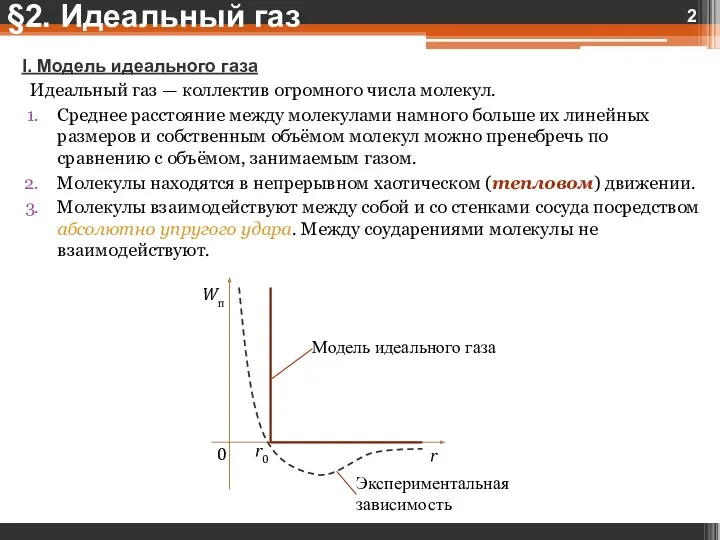
I. Модель идеального газа
Идеальный газ — коллектив огромного числа молекул.
Среднее расстояние между молекулами намного больше их линейных размеров и собственным объёмом молекул можно пренебречь по сравнению с объёмом, занимаемым газом.
Молекулы находятся в непрерывном хаотическом (тепловом) движении.
Молекулы взаимодействуют между собой и со стенками сосуда посредством абсолютно упругого удара. Между соударениями молекулы не взаимодействуют.
§2. Идеальный газ

§2. Идеальный газ
II. Уравнение состояния идеального газа. Газовые законы
Уравнение состояния идеального газа:
Частные случаи (газовые законы):
T = const: — закон Бойля-Мариотта
p = const: — закон Гей-Люссака
V = const: — закон Шарля
— уравнение Менделеева-Клапейрона
— универсальная газовая постоянная

§2. Идеальный газ
— постоянная Больцмана
Концентрация молекул — ФВ — характеристика макросистемы, равная числу частиц в единичном объёме:
Закон Дальтона: давление смеси газов равно сумме парциальных давлений компонент смеси:
Доказательство
Нормальные условия: p0 = 1,01·105 Па; T0 = 273 К

III. Основное уравнение МКТ
Рассмотрим равновесный идеальный газ, состоящий из одинаковых молекул массой m0. Все молекулы имеют разные по модулю и направлению скорости. Давление газа обусловлено ударами молекул о стенку сосуда.
1. Удар одной молекулы
Удар молекулы о стенку — абсолютно упругий.
II закон Ньютона:
— сила, с которой стенка действует на молекулу
τ — время удара
III закон Ньютона:
§2. Идеальный газ

2. Число ударов о стенку за время Δt >> τ
i-я скоростная группа молекул: v = (vi, vi ± Δv)
Число молекул внутри цилиндра, которые долетят до стенки за время Δt:
ni — концентрация молекул i-ой скоростной группы
Коэффициент 1/6 из всех молекул 1/3 движется вдоль оси x, из них ½ движется в направлении стенки.
3. Импульс, полученный стенкой от молекул i-ой скоростной группы за время Δt
Fi — модуль суммарной силы, с которой молекулы i-ой скоростной группы действуют на участок стенки площадью ΔS
Давление молекул i-ой скоростной группы
§2. Идеальный газ

4. Учёт давления всех скоростных групп молекул
Закон Дальтона:
— средняя квадратичная скорость молекулы идеального газа
— основное уравнение МКТ идеального газа
— основное уравнение МКТ идеального газа для энергии
— средняя кинетическая энергия поступательного движения молекулы идеального газа
§2. Идеальный газ