Содержание
- 2. ЛЕКЦИЯ 1 ФИЗИКА КОЛЕБАНИЙ *
- 3. *
- 4. * Механические колебания Колебательные процессы весьма часто встречаются в окружающей нас природе и технике. Значительная часть
- 5. *
- 6. Колебания (колебательные движения)- изменения состояния, обладающие той или иной степенью повторяемости во времени. КОЛЕБАНИЯ Колебания могут
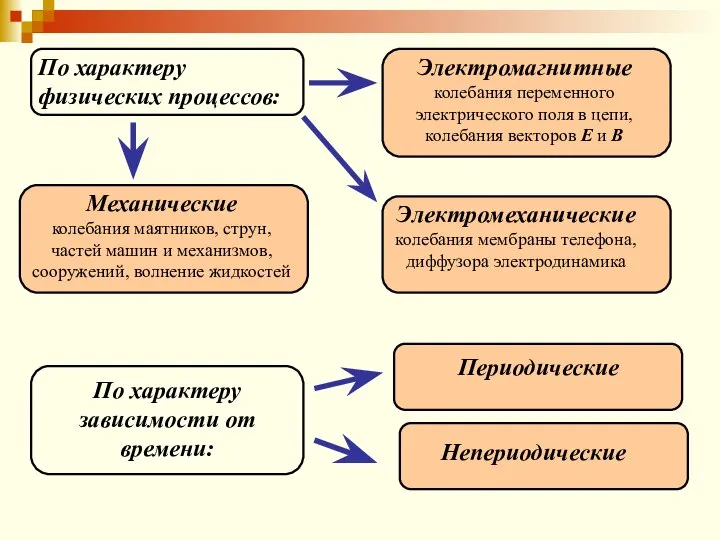
- 7. По характеру физических процессов: Электромагнитные колебания переменного электрического поля в цепи, колебания векторов Е и В
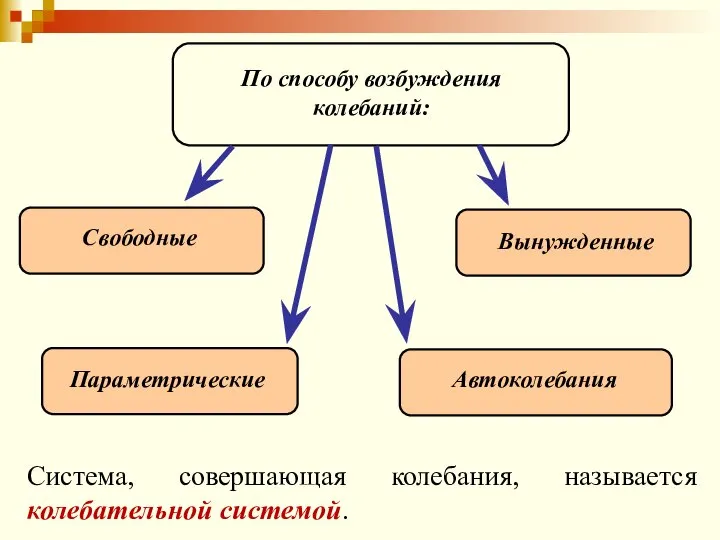
- 8. По способу возбуждения колебаний: Свободные Вынужденные Параметрические Автоколебания Система, совершающая колебания, называется колебательной системой.
- 9. Свободные (или собственные) — это колебания в системе не подверженных действию переменных внешних сил, под действием
- 10. Условия возникновения свободных колебаний 1. Колебательная система должна иметь положение устойчивого равновесия. 2. При выведении системы
- 11. * Параметрические — колебания, возникаю-щие при изменении какого-либо параметра колебательной системы в результате внешнего воздействия. Вынужденные
- 12. * Автоколебания — колебания, при которых система имеет запас потенциальной энергии, расходующейся на совершение колебаний (пример
- 13. * Колебания - периодические, если значения физических величин, изменяющихся в процессе колебаний, повторяются через равные промежутки
- 14. Периодические процессы можно представить как наложение гармонических колебаний. Фурье установил, что любое периодическое негармоническое колебание может
- 15. * Гармонические колебания – колебания, при которых колеблющаяся величина изменяется со временем по закону синуса или
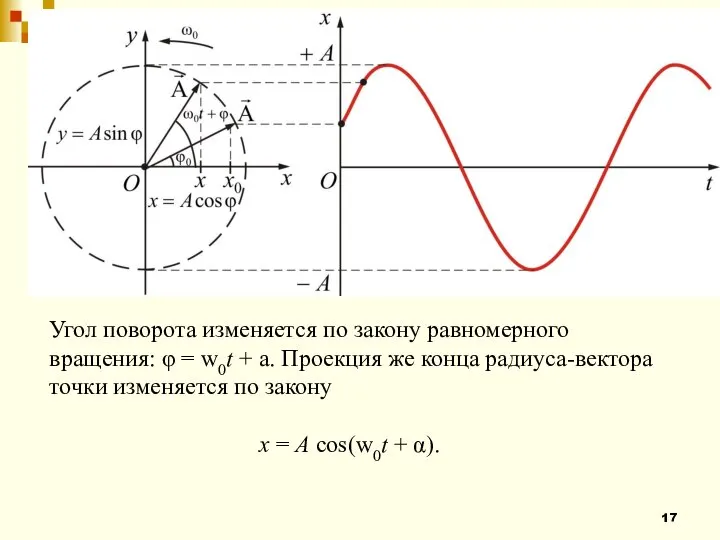
- 16. * Простейшей моделью гармонического колебания является колебание проекции x конца радиуса-вектора r точки, движущейся по окружности
- 17. Угол поворота изменяется по закону равномерного вращения: φ = w0t + a. Проекция же конца радиуса-вектора
- 18. Если некоторая материальная точка совершает гармоническое колебательное движение около положения равновесия вдоль некоторой оси x (гармонический
- 19. Характеристики колебательного движения 1. Амплитуда 2. Период 3. Частота *
- 20. Период колебаний - (Т) наименьший промежуток времени, через который повторяются значения всех физических величин, характеризующих колебательное
- 21. * Амплитуда - Наибольшее (по модулю) отклонение колеблющегося тела от положения равновесия Циклическая ( круговая частота)
- 22. Механические гармонические колебания Гармонические колебания – простейшие периодические колебания, при которых координата тела меняется по закону
- 23. Если в начальный момент времени тело проходит положение равновесия, то колебания являются синусоидальными. Рассмотрим прямолинейные гармоничес-кие
- 24. Кинематика колебаний Циклическая частота связана с линейной частотой и периодом следующими соотношениями *
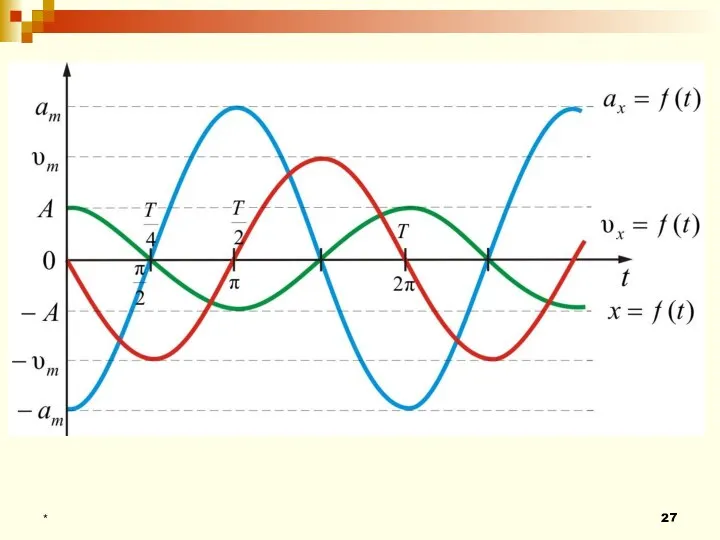
- 25. Скорость колеблющейся точки меняется по закону:
- 26. Ускорение:
- 27. *
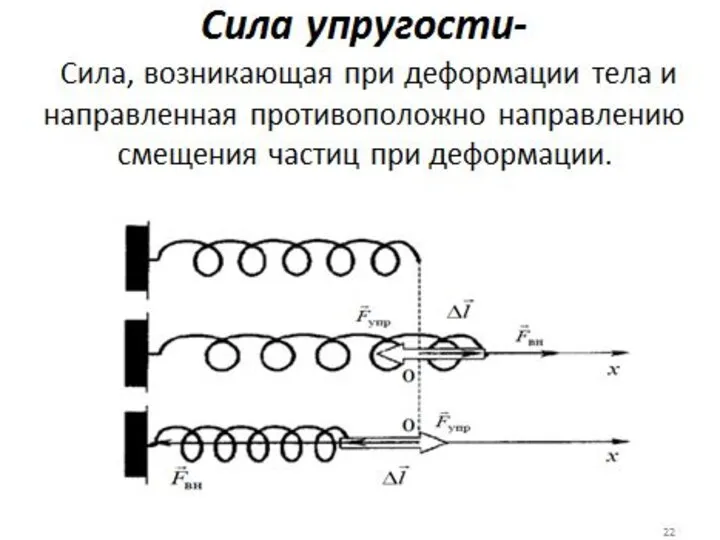
- 28. Сила, вызывающая колебания, обладает следующими свойствами 2. модуль силы пропорционален смещению материальной точки из положения равновесия;
- 29. Такие силы называют возвращающими. Зависимость характерна для упругой силы. F = -kx Следовательно, сила всегда направлена
- 30. *
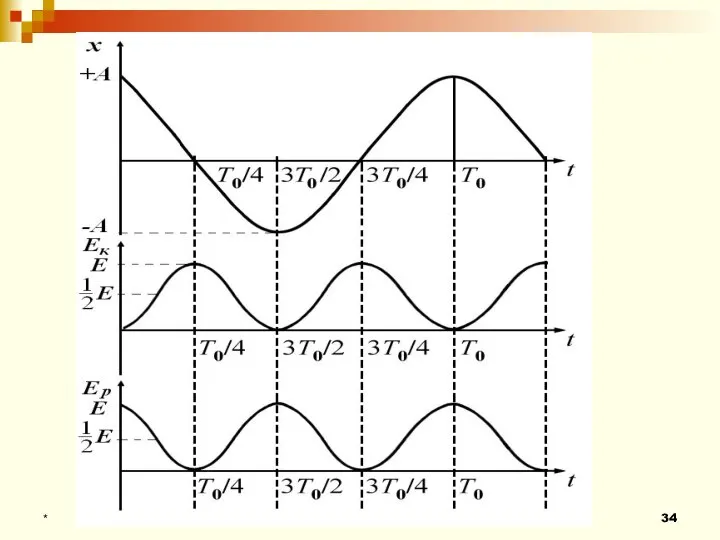
- 31. ЭНЕРГИЯ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ Кинетическая энергия материальной точки, совершающей гармонические колебания:
- 32. Потенциальная энергия материальной точки, совершающей гармонические колебания под действием упругой силы F:
- 33. Полная энергия: где
- 34. *
- 35. Гармонический осциллятор Осциллятор – система, совершающая свободные колебания. Классический осциллятор – механическая система, совершающая колебания около
- 36. Дифференциальное уравнение гармонического осциллятора Решение этого уравнения: Здесь x – колеблющаяся величина.
- 37. Маятники Маятник- тело, совершающее колебания относительно положения равновесия под действием приложенных к нему сил. Пружинный маятник
- 38. Пружинный маятник это закреплённый на пружине груз, способный совершать колебания в вертикальном или горизонтальном или направлении.
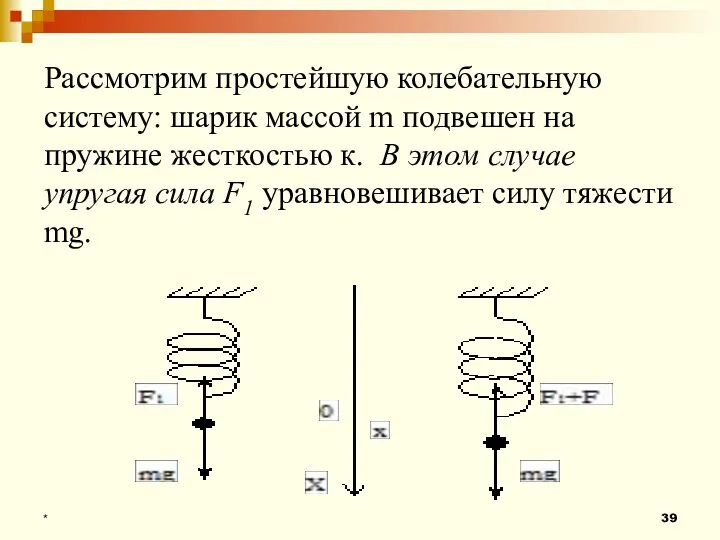
- 39. * Рассмотрим простейшую колебательную систему: шарик массой m подвешен на пружине жесткостью к. В этом случае
- 40. * Изменение упругой силы по закону Гука пропорционально изменению длины пружины или смещению шарика х: F=-kx,(1)
- 41. * Уравнение второго закона Ньютона для шарика имеет вид: Введем обозначения Тогда Решение уравнения имеет вид
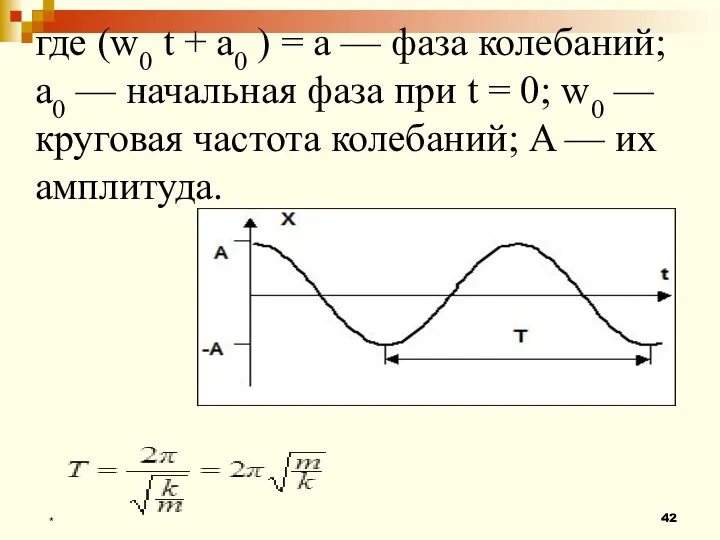
- 42. * где (w0 t + a0 ) = a — фаза колебаний; a0 — начальная фаза
- 43. Решив данное уравнение, получим, что пружинный маятник совершает гармонические колебания по закону x = A cos(ω0t
- 44. * В горизонтальном направлении на груз действует только сила упругости со стороны пружины. Второй закон Ньютона
- 45. Физический маятник Твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной горизонтальной оси, проходящей через
- 46. тела момент M возвращающей силы можно записать в виде (1) где J — момент инерции маятника
- 47. * решение которого : При малых колебаниях физический маятник совершает гармонические колебания с периодом где L=J/(ml)
- 48. J – момент инерции маятника относительно оси, проходящей через точку подвеса. Приведенная длина физического маятника –
- 49. * Применяя теорему Штейнера, получим т. е. ОО' всегда больше ОС. Точка подвеса О маятника и
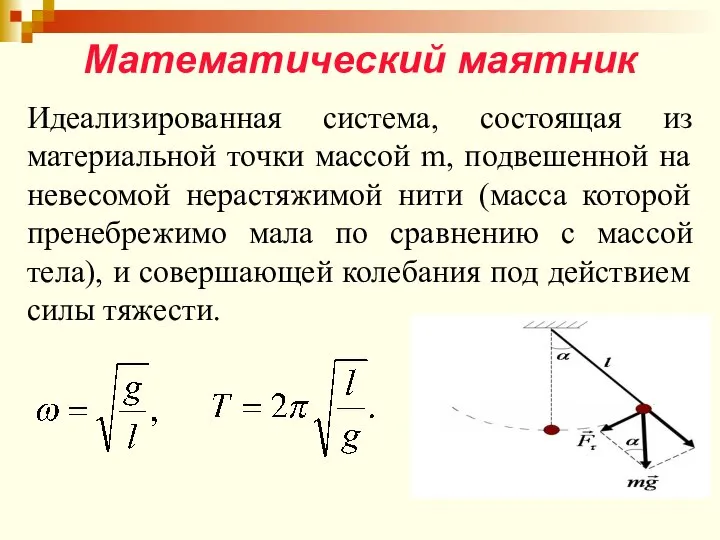
- 50. Математический маятник Идеализированная система, состоящая из материальной точки массой m, подвешенной на невесомой нерастяжимой нити (масса
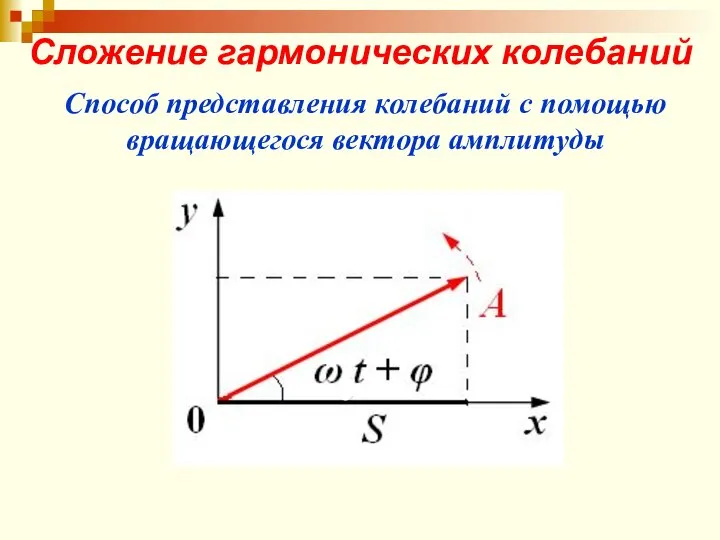
- 51. Сложение гармонических колебаний Способ представления колебаний с помощью вращающегося вектора амплитуды
- 52. Сложение двух одинаково направленных колебаний 1. Сложение гармонических колебаний одного направления и одинаковой частоты Разность фаз
- 53. Для нахождения результирующего колебания воспользуемся методом векторных диаграмм.
- 54. Если колебания синфазны: φ2 – φ1 = ±2mπ, следовательно, А = А1 + А2, происходит усиление
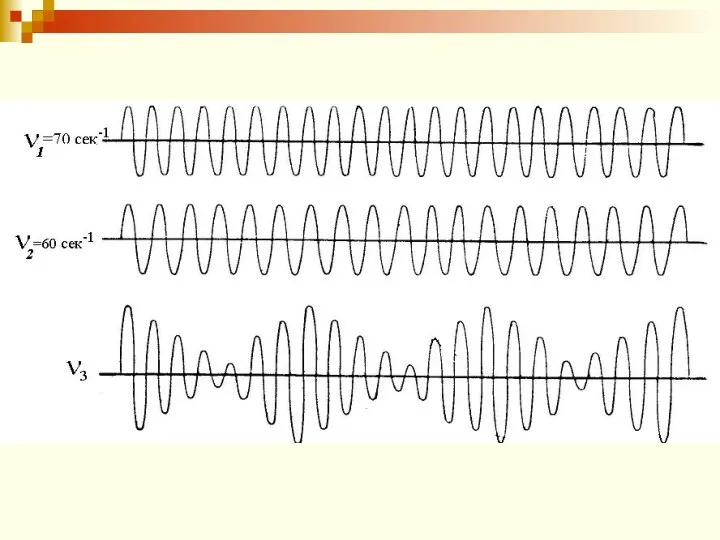
- 55. 2. Сложение гармонических колебаний одного направления с частотами неравными, но близкими - биения Если амплитуды двух
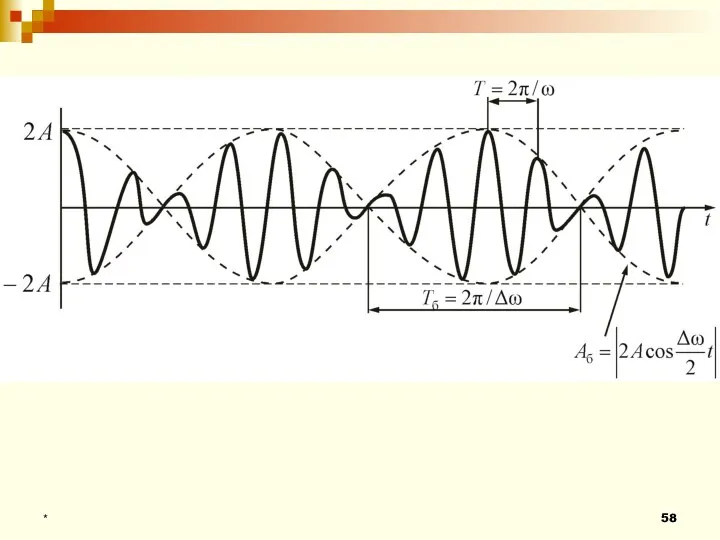
- 56. * Периодические изменения амплитуды от минимального значения до максимального называются биениями. Уравнение результирующего колебания
- 57. * Результирующее колебание можно рассматривать как гармоническое с частотой ω, амплитуда Аб которого изменяется по периодическому
- 58. *
- 60. Гармонические колебания совпадают по направлению и имеют кратные циклические частоты ω, 2ω, 3ω и т.д. В
- 61. * Такое представление периодической функции f(t) называется разложением функции в ряд Фурье или гармоническим анализом сложного
- 62. 3. Сложение взаимно перпендикулярных колебаний Сложение колебаний с одинаковыми частотами (ω1 :ω2=1:1 ) Пусть точка одновременно
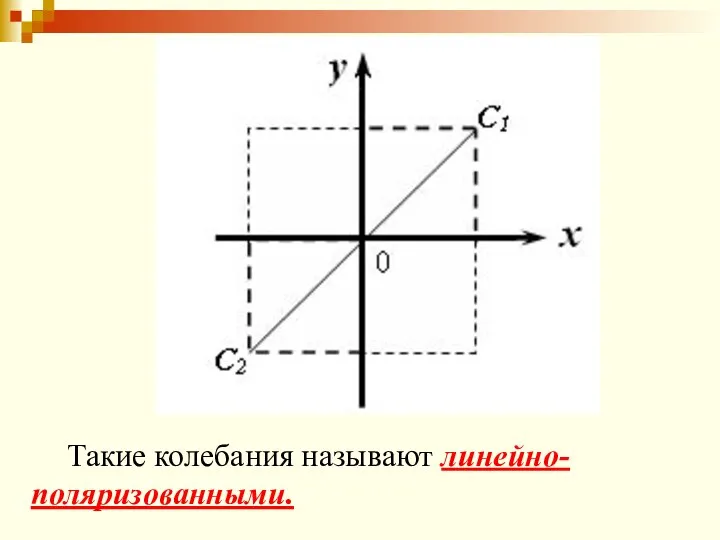
- 63. Рассмотрим несколько частных случаев: 1) Фазы колебаний равны. x = A1 sin ωt; y = A2
- 64. Такие колебания называют линейно-поляризованными.
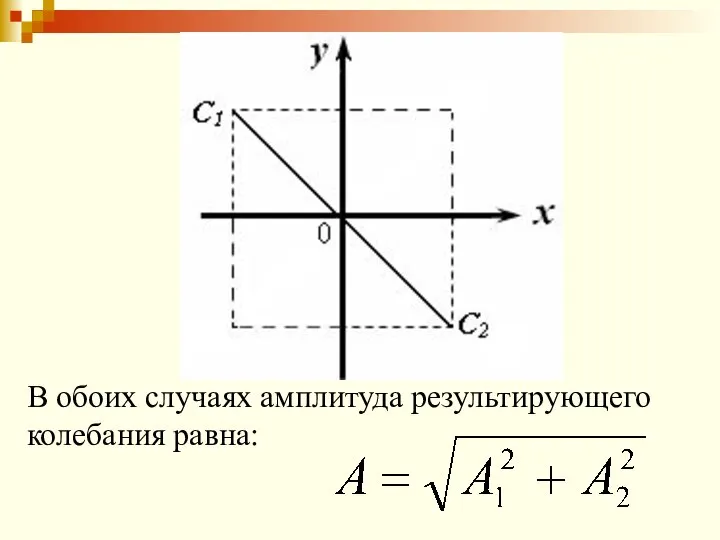
- 65. 2) Разность фаз равна π. x = A1 sin (ωt + π) = - A1 sin
- 66. В обоих случаях амплитуда результирующего колебания равна:
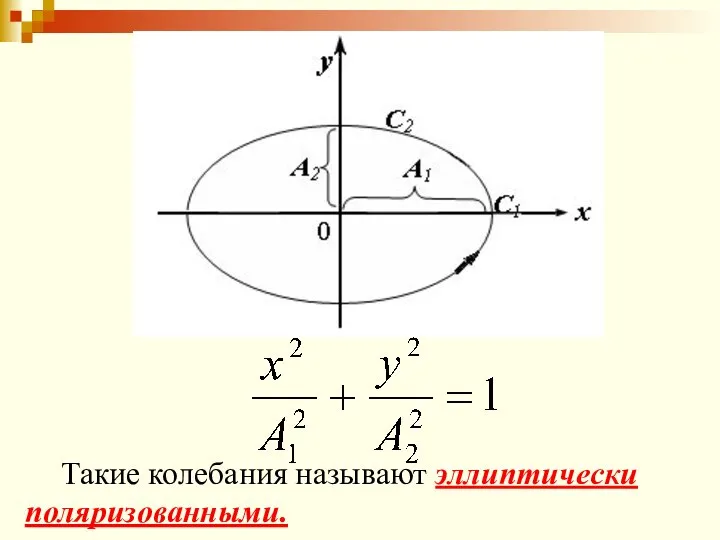
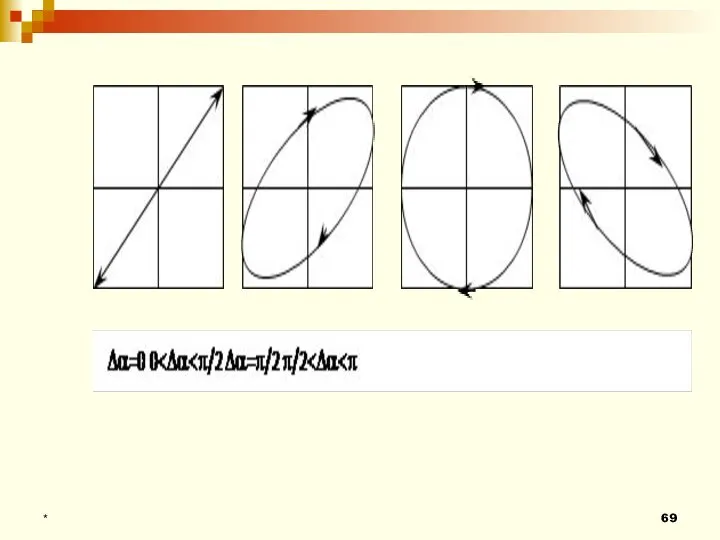
- 67. 3) Разность фаз равна π/2.
- 68. Такие колебания называют эллиптически поляризованными.
- 69. *
- 70. Если частоты складываемых колебаний относятся друг к другу как целые числа, то траектория результирующего движения оказывается
- 71. *
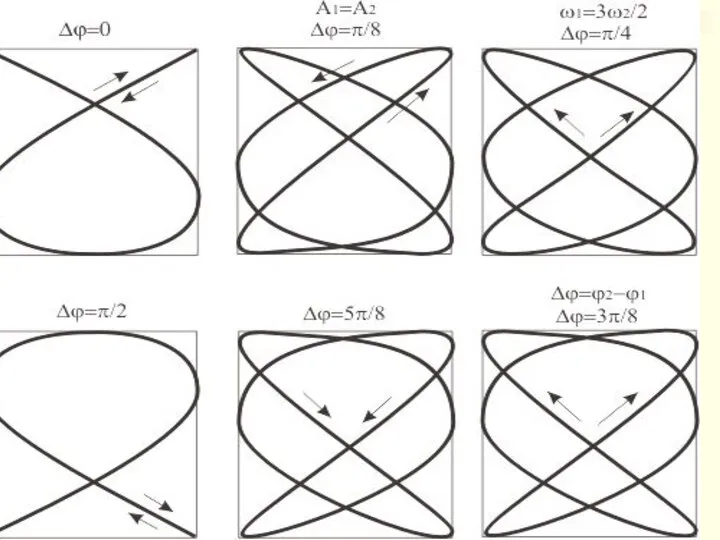
- 72. По виду фигур можно определить неизвестную частоту по известной, или определить отношение частот складываемых колебаний. Отношение
- 73. * Фигуры Лиссажу при
- 74. Затухающие колебания Затухающие колебания – колебания, амплитуда которых из-за потерь энергии реальной колебательной системой с течением
- 75. Закон затухания колебаний определяется свойствами колебательных систем. Обычно рассматриваются линейные системы – идеализированные реальные системы, в
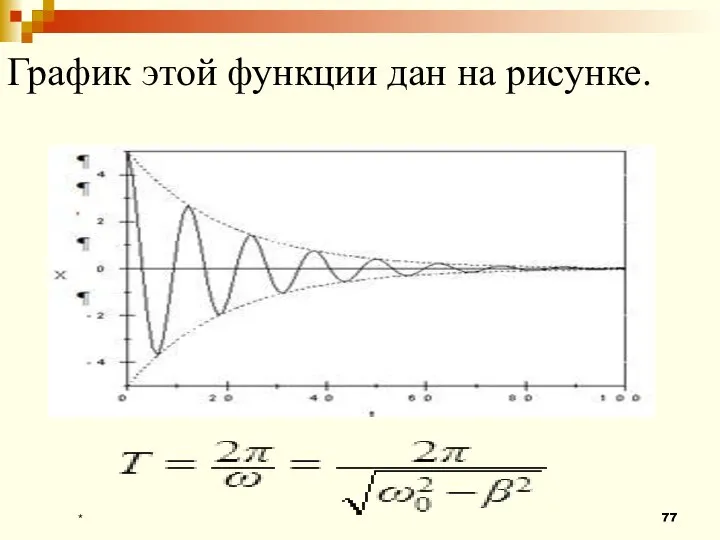
- 76. * Дифференциальное уравнение свободных затухающих колебаний линейной системы: х – колеблющаяся величина, β = const –
- 77. * График этой функции дан на рисунке.
- 78. Для пружинного маятника массой m, совершающего малые колебания под действием упругой силы, сила трения пропорциональна скорости:
- 79. Амплитуда затухающих колебаний: Это отношение называют декрементом затухания . В качестве меры затухания часто берут величину
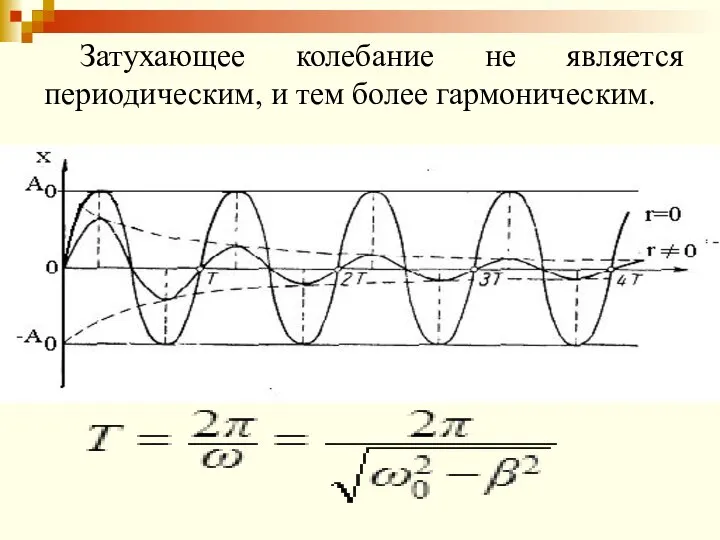
- 80. Затухающее колебание не является периодическим, и тем более гармоническим.
- 81. Вынужденные колебания Вынужденные колебания – незатухающие колебания, возникающие под действием периодической силы, изменяющейся по гармоническому закону:
- 82. Для простейшего пружинного маятника, на который действует внешняя сила Дифференциальное уравнение вынужденных колебаний маятника: :
- 83. В установившемся режиме вынужденные колебания являются гармоническими, происходят с частотой внешней гармонической силы.
- 84. В случае установившихся колебаний при некоторой частоте внешней силы – резонансной частоте ωрез – амплитуда смещения
- 86. Скачать презентацию


























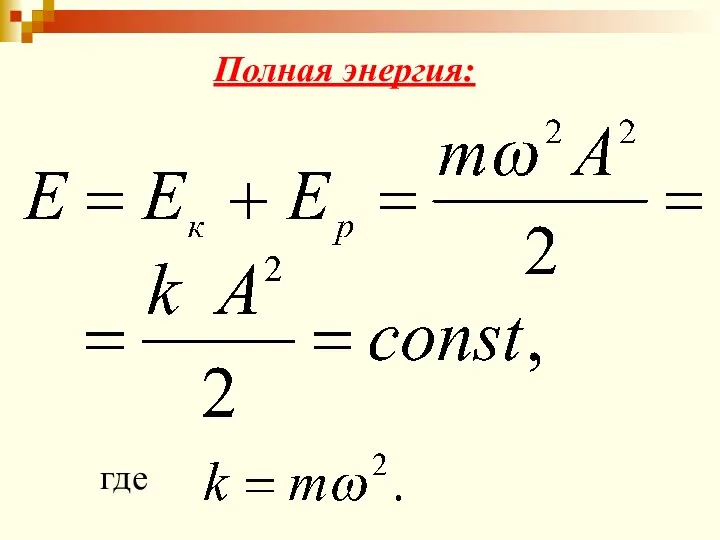





































 ДМА – динамически механический анализ
ДМА – динамически механический анализ Ядерные реакции
Ядерные реакции Законы сохранения
Законы сохранения Радиоактивность. Виды радиоактивного облучения
Радиоактивность. Виды радиоактивного облучения Ультрофеолетовые волны
Ультрофеолетовые волны Последовательное и параллельное соединения проводников
Последовательное и параллельное соединения проводников Электромагнитные волны
Электромагнитные волны Судостроение. Что общего у предметов?
Судостроение. Что общего у предметов?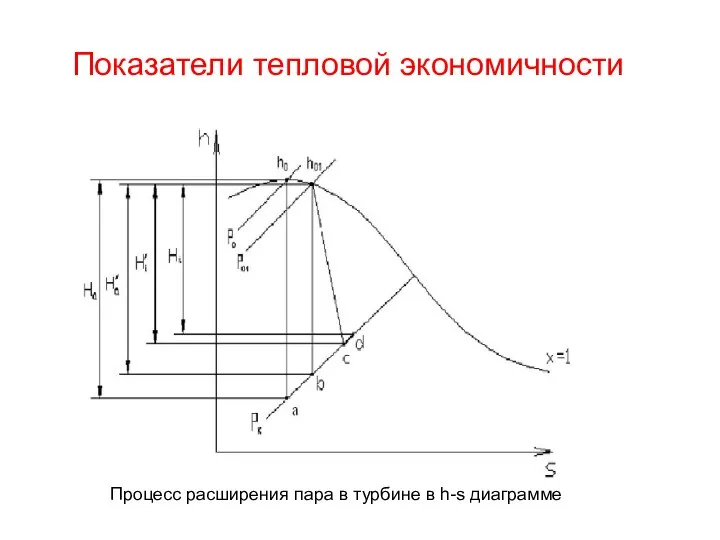 Показатели тепловой экономичности
Показатели тепловой экономичности Реактивное движение. Ракеты
Реактивное движение. Ракеты МотоСкороХоды
МотоСкороХоды Электроёмкость Конденсатор Энергия конденсатора
Электроёмкость Конденсатор Энергия конденсатора Tok energie
Tok energie Действительные циклы ДВС
Действительные циклы ДВС Работа и потенциал электростатического поля. 10 класс
Работа и потенциал электростатического поля. 10 класс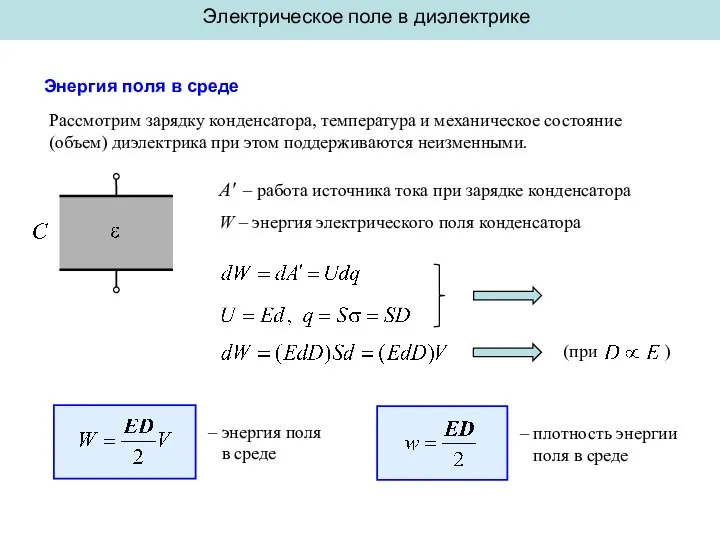 Энергия поля в среде
Энергия поля в среде Кинематика. Решение задач
Кинематика. Решение задач Электростатика. Диагностико-коррекционный тест. 8 класс
Электростатика. Диагностико-коррекционный тест. 8 класс Теплообмен при поперечном обтекании труб и пучков
Теплообмен при поперечном обтекании труб и пучков Инструкция по сборке прицепа серии Стандарт и профи
Инструкция по сборке прицепа серии Стандарт и профи УФ-спектроскопия. Часть 1
УФ-спектроскопия. Часть 1 Как научиться решать задачи по физике
Как научиться решать задачи по физике Микронометр
Микронометр Urok_Osnovy_MKT
Urok_Osnovy_MKT Электроёмкость. Конденсаторы
Электроёмкость. Конденсаторы Волновые свойства света
Волновые свойства света Уравнение газового состояния
Уравнение газового состояния Презентация на тему Атмосферное давление: практикум
Презентация на тему Атмосферное давление: практикум