Метод расчета переходных процессов в линейной электрической цепи

В классическом методе расчета отдельно рассчитывают принужденные и свободные составляющие токов и напряжений, а общее решение представляет собой сумму принужденной и свободной составляющих. Определение постоянных интегрирования, входящих в выражение для свободного тока (напряжения), производят путем совместного решения системы линейных алгебраических уравнений по известным значениям корней характеристического уравнения, а также по известным значениям свободной составляющей тока (напряжения) и их производных, взятых при t = 0+.

ОПРЕДЕЛЕНИЕ ПОСТОЯННЫХ ИНТЕГРИРОВАНИЯ В КЛАССИЧЕСКОМ МЕТОДЕ
Для любой схемы с помощью уравнений Кирхгофа и законов коммутации можно найти:
числовое значение искомого свободного тока при t = 0+, обозначим его iсв(0+);
числовое значение первой, а если понадобится, то и высших производных от свободного тока, взятых при t = 0+. Числовое значение первой производной от свободного тока при t = 0+ обозначим i′св (0+); второй – i′′св(0+); и т. д.
Рассмотрим способ определения постоянных интегрирования A1,A2,..., полагая известными iсв(0+), i′св(0+), i′′св(0+) и значения корней p1, p2, ....

Если характеристическое уравнение цепи представляет собой уравнение первой степени, то iсв = Aept. Постоянную интегрирования А определяют по значению свободного тока iсв(0+):
A = iсв(0+). (18)
Если дано характеристическое уравнение второй степени и его корни действительны и не равны, то
(19)
Продифференцируем это уравнение по времени:
(20)

Запишем уравнения (19) и (20) для момента коммутации t = 0+ с учетом, того, что при t = 0+
В результате получим
(21)
(22)
В этой системе уравнений известными являются его iсв(0+), i′св(0+), p1 и p2, неизвестными – А1 и А2
Совместное решение (21) и (22) дает
(23)

Для цепи, имеющей характеристическое уравнение третьей степени, свободный ток
(24)
Найдем первую и вторую производные от обеих частей уравнения (20):
(25)
(26)
Запишем (24) – (26) при t = 0+:
(27)

Система уравнений (27) представляет собой систему трех линейных алгебраических уравнений с тремя неизвестными: А1, А2 и А3. Все остальные входящие в нее величины [p1, p2, p3, iсв(0+), i′св(0+), i′′св(0+)] известны.
При двух корнях характеристического уравнения для определения постоянных интегрирования достаточно, чтобы были известны величины свободных токов и напряжений и их производных. Величины свободных составляющих определяются как разность начальных условий и принужденных составляющих при t = 0+. Согласно (8)
i(0+) = iПР(0+) + iCB(0+),
откуда
iCB(0+) = i(0+) – iПР(0+) = А1 + А2

Производные токов и напряжений найдем из выражений напряжения на индуктивности и тока через емкость.
откуда
Определение третьих производных токов и напряжений и выше достаточно сложно, поэтому классический метод расчета переходных процессов в электрических цепях применения не нашел.

ПЕРЕХОДНЫЙ ПРОЦЕСС В RL–ЦЕПИ
ПРИ ВКЛЮЧЕНИИ ЭДС
Рассмотрим электрическую цепь, изображенную на рис. 12.
Так как ток через индуктивность не может измениться скачком, то в момент времени t(0+) тока в цепи нет. Поэтому в схеме для определения начальных условий индуктивность можно заменить разрывом. Начальными условиями являются: i(0+) = 0; uL(0+) = e(0–).

Характеристическое уравнение имеет вид
r + pL = 0,
и соответственно корень характеристического уравнения Переходный ток в цепи равен сумме принужденной и свободной составляющей, которые определяются через e(t), r и L.
где .
Рассмотрим случаи, когда ЭДС постоянная и равна Е и когда она синусоидальная e(t) = Emsin(ωt + Ψ).
При включении цепи к постоянной ЭДС принужденная
составляющая тока равна ,
поскольку сопротивление индуктивности постоянному току равно нулю.

Постоянная интегрирования А находится из начальных условий при t = 0(+).
откуда .
Таким образом, переходный ток в цепи равен
Переходное напряжение на индуктивности выразится как

При постоянной ЭДС в цепи принужденная составляющая напряжения равна нулю, поэтому
откуда А = Е.
Таким образом, переходное напряжение на индуктивности выражается как
Графики принужденной составляющей тока, свободных и полных составляющих тока и напряжения приведены на рис. 13.

При включении синусоидальной ЭДС e = Emsin(ωt + Ψ) характеристическое уравнение остается тем же, так как определяется только параметрами цепи и не зависит от величин и фаз источников электрической энергии. Не изменяется также схема цепи для определения начальных условий (рис. 12, б).
Определим начальные условия.
i(0+) = i(0–) =0; uL(0+) = .
Принужденные составляющие определятся символическим методом через комплексные величины
где

Комплексному значению принужденного тока соответствует мгновенное:
Постоянная интегрирования определяется из уравнения
При нулевом значении i(0+)
Переходной ток

Свободная составляющая напряжения на индуктивности будет изменяться по экспоненциальному закону как
Графики принужденной составляющей тока, свободных и полных составляющих тока и напряжения приведены на рис. 14.

Анализ уравнения для свободного тока показывает, что его начальное значение зависит от соотношения активного и реактивного сопротивлений и от начальной фазы ЭДС. Начальное значение свободного тока тем меньше, чем меньше разность Ψ - ϕ. Если эта разность равна нулю или p, будет равна нулю и свободная составляющая тока, т.е., переходного тока при подключении синусоидальной ЭДС не будет. А так как напряжение на индуктивности равно произведению индуктивности на производную тока, не будет и переходного напряжения, т.е., переходного процесса в цепи не будет.
В цепях синусоидального тока при коммутациях могут быть случаи, когда переходного процесса не будет.

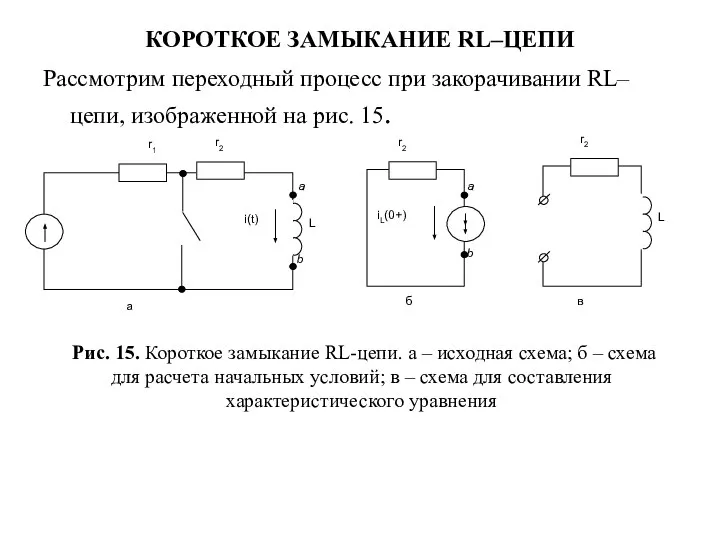
КОРОТКОЕ ЗАМЫКАНИЕ RL–ЦЕПИ
Рассмотрим переходный процесс при закорачивании RL–цепи, изображенной на рис. 15.
Рис. 15. Короткое замыкание RL-цепи. а – исходная схема; б – схема для расчета начальных условий; в – схема для составления характеристического уравнения
в

В отличие от предыдущей задачи в этой независимые начальные условия ненулевые. Через индуктивность протекает ток, определяемый суммой активных сопротивлений, если в цепи включена ЭДС постоянного тока, и комплексным сопротивлением, если ЭДС синусоидальная. Рассмотрим оба случая.
При постоянной ЭДС ток через индуктивность до коммутации
,
при синусоидальной комплексное значение докоммутационного тока
где

Мгновенное значение тока при t = 0+ получается как
Коммутацией ключа цепь делится на две, между собой не связанные: левая состоит из ЭДС и сопротивления r1; правая из сопротивления r2 и индуктивности L. Переходный процесс имеет место только в правой части, где имеется индуктивность. Так как в этой части цепи отсутствуют источники электрической энергии, то принужденные составляющие токов и напряжений равны нулю. Следовательно, переходные ток и напряжение равны соответственно свободному току и свободному напряжению.

Характеристическое уравнение получаем через операторное сопротивление, разомкнутой послекоммутационной схемы (рис.15, в):
Z(p) = r2 + pL,
откуда .
Переходный ток при постоянной ЭДС
,
при синусоидальной

Напряжение на индуктивности равно напряжению на сопротивлении r Оно выражается соответственно при постоянной и синусоидальной ЭДС как

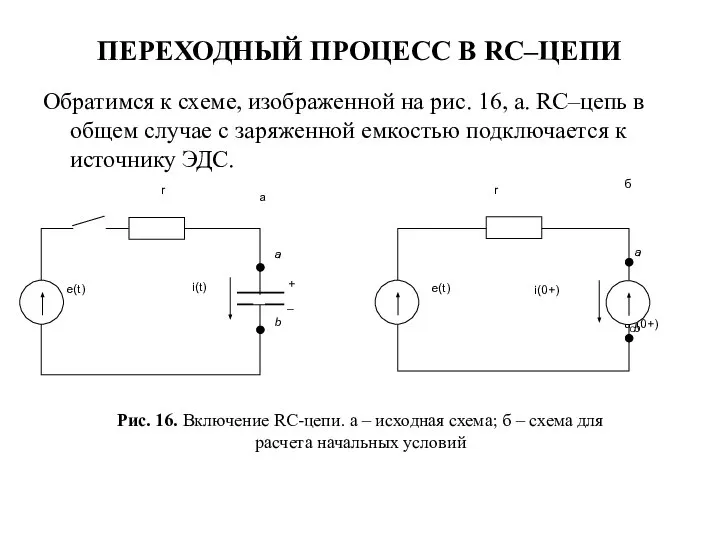
ПЕРЕХОДНЫЙ ПРОЦЕСС В RC–ЦЕПИ
Обратимся к схеме, изображенной на рис. 16, а. RC–цепь в общем случае с заряженной емкостью подключается к источнику ЭДС.

Согласно второму закону коммутации напряжение на емкости до коммутации, равное при заданном заряде , остается тем же после коммутации. Если емкость не заряжена (подавляющее большинство цепей) напряжение на ней равно нулю. Этот параметр является независимым начальным условием. Зависимым начальным условием является ток в цепи:
Характеристическое уравнение имеет вид:
откуда . Постоянная времени t = rC.

Принужденное напряжение на незаряженной емкости при постоянной ЭДС
Если включена синусоидальная ЭДС, принужденные составляющие тока и напряжения на емкости вычислим сначала в комплексной форме записи, из которых получим мгновенные значения:

Постоянная интегрирования А равна разности начального условия и принужденной составляющей в момент времени t(0+). При постоянной ЭДС в цепи с незаряженной емкостью постоянная интегрирования напряжения на емкости
А = – Е,
при синусоидальной ЭДС
Соответственно постоянные интегрирования токов:

Переходные напряжение и ток при включении постоянной ЭДС:
Если включается синусоидальная ЭДС, получаем:

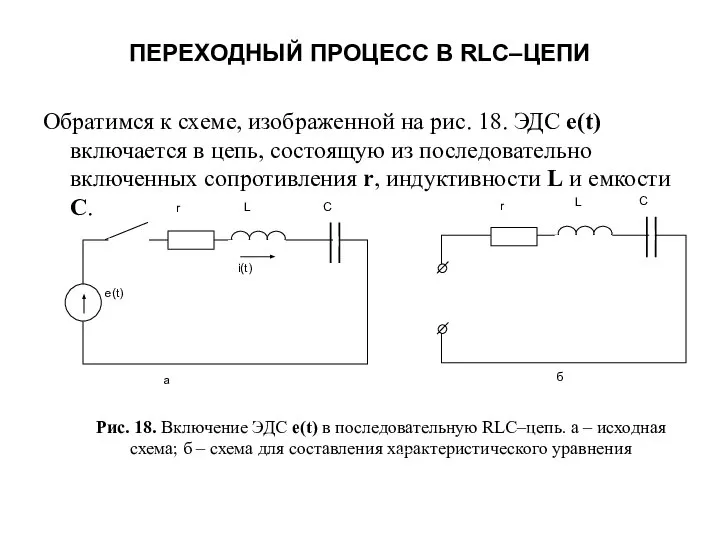
ПЕРЕХОДНЫЙ ПРОЦЕСС В RLC–ЦЕПИ
Обратимся к схеме, изображенной на рис. 18. ЭДС е(t) включается в цепь, состоящую из последовательно включенных сопротивления r, индуктивности L и емкости С.

Характеристическое уравнение
имеет корни:
где – резонансная частота.
Поскольку имеем два корня характеристического уравнения, свободный ток
а ток в цепи

Принужденный ток определяется через заданную ЭДС и параметры пассивных элементов.
В зависимости от соотношения δ и ω0 свободные токи и напряжения буду затухать либо апериодически, либо колебательно. Если δ > ω0, корни характеристического уравнения будут отрицательными действительными, если δ < ω0 – комплексно сопряженными с отрицательной действительной частью, В первом случае процесс затухания свободных токов и напряжений апериодический, во втором – колебательный. Примеры затухания свободных составляющих приведены на рис. 19.

Если RLC – цепь подключается к источнику синусоидальной ЭДС, то принужденный ток
iПР(t) = Imsin(ωt + Ψ – ϕ),
а полный
Характер переходного процесса зависит только от параметров пассивных элементов, но не от вида и величины ЭДС. Переходные токи и напряжения могут стремиться к принужденным либо апериодически, либо колебательно. При этом свободная частота может быть больше принужденной, или меньше. На рис 20 показаны случаи апериодического и колебательного переходного процесса.

РАСЧЕТ ПЕРЕХОДНОГО ПРОЦЕССА В
РАЗВВЕТВЛЕННОЙ ЦЕПИ
В классическом методе расчета переходных процессов отдельно рассчитываются принужденные составляющие токов и напряжений, отдельно – свободные.
Принужденные составляющие определяются через величины источников тока и ЭДС и параметры пассивных элементов цепи. Если источники электрической энергии синусоидальны, расчет производится символическим методом с последующим переводом комплексных величин в мгновенные синусоидальные.
Постоянные интегрирования свободных составляющих токов и напряжений определяются через разности начальных значений в момент времени t = 0+ и принужденных составляющих в этот же момент времени.