Качественные методы исследования нелинейных систем. Устойчивость положения равновесия динамических систем

Содержание
1. Устойчивость положения равновесия динамических систем
2. Замкнутые фазовые траектории
3.Диссипативные системы
4.Бифуркация динамических систем

1.Устойчивость положения равновесия динамических систем

2. Замкнутые фазовые траектории
Наряду с положениями равновесия замкнутые фазовые траектории играют исключительно важную роль в теории колебаний, поскольку они отображают периодические движения реальных систем.
Замкнутые фазовые траектории бывают изолированными и неизолированными.
Определение 2. 1. Замкнутая фазовая траектория называется изолированной, если существует такая достаточно малая (кольцеобразная) ее окрестность, внутри которой нет других замкнутых фазовых траекторий. (На рис. граница этой окрестности обозначена штриховыми линиями.)

Определение 2. 2. Замкнутая фазовая траектория называется неизолированной, если в сколь угодно малой (кольцеобразной) ее окрестности находятся другие замкнутые фазовые траектории.
Определение 2.3. Замкнутая изолированная фазовая траектория называется предельным циклом.

3.Диссипативные системы

4.Бифуркация динамических систем
Теория бифуркаций динамических систем — это теория, которая изучает изменения качественной картины разбиения фазового пространства в зависимости от изменения параметра (или нескольких параметров).
Бифуркация — это приобретение нового качества в движениях динамической системы при малом изменении её параметров.
Центральным понятием теории бифуркации является понятие (не)грубой системы. Берётся какая-либо динамическая система и рассматривается такое (много)параметрическое семейство динамических систем, что исходная система получается в качестве частного случая — при каком-либо одном значении параметра. Если при значении параметров, достаточно близких к данному, сохраняется качественная картина разбиения фазового пространства на траектории, то такая система называется грубой. В противном случае, если такой окрестности не существует, то система называется негрубой.

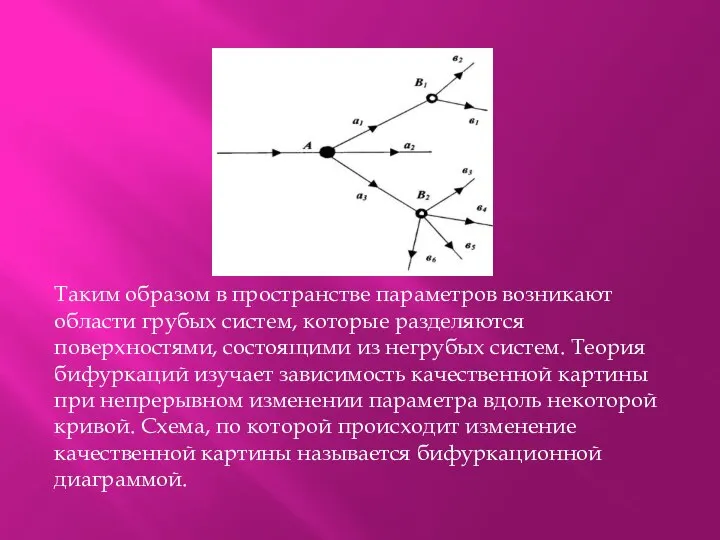
Таким образом в пространстве параметров возникают области грубых систем, которые разделяются поверхностями, состоящими из негрубых систем. Теория бифуркаций изучает зависимость качественной картины при непрерывном изменении параметра вдоль некоторой кривой. Схема, по которой происходит изменение качественной картины называется бифуркационной диаграммой.