Содержание
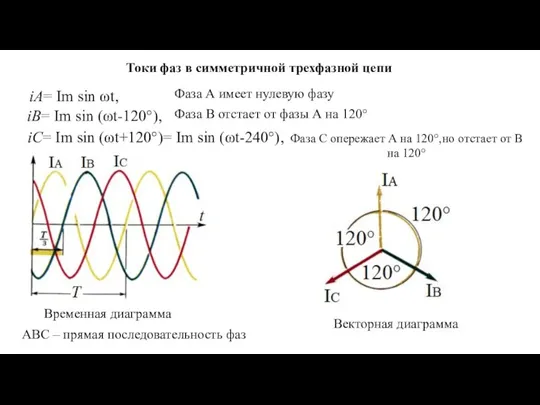
- 2. iА= Im sin ωt, Токи фаз в симметричной трехфазной цепи iВ= Im sin (ωt-120°), iС= Im
- 3. Перейдем к комплексной форме записи: Просуммируем фазные токи: Основное свойство 3-х фазной цепи
- 4. Ток фазы А в любой момент времени возвращается по фазам В и С. Роль обратного провода
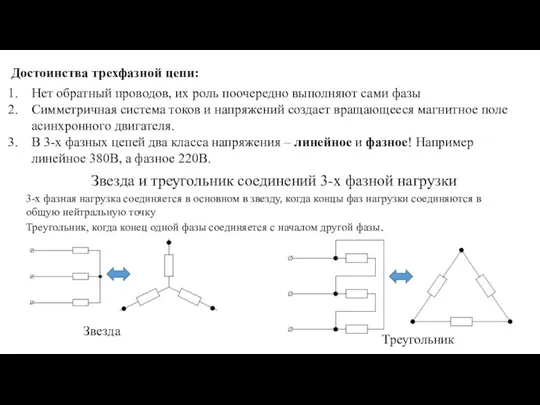
- 5. Достоинства трехфазной цепи: Нет обратный проводов, их роль поочередно выполняют сами фазы Симметричная система токов и
- 6. Подключение источника и приемника звездой N,n – нейтраль или нейтральна точка источника и приемника, соответственно IA,
- 7. Подключение источника и приемника треугольником Определим линейные токи через фазные, записав первый закон Кирхгофа для узлов
- 8. Расчет 3-х фазной несимметричной цепи соединенной звездой Не симметрия 3-х фазной цепи нежелательное, но неизбежное событие,
- 9. Линейные токи найдём по закону Ома В частном случае, когда сопротивление фаз одинаковы (ZA=ZB=Zc=Z): Напряжение смещения
- 10. Пусть 3-х фазная система симметрична, а сопротивление фаз одинаковые Построим векторную диаграмму для этого случая. Пусть
- 11. Расчет 3-х фазной несимметричной цепи соединенной треугольником Расчет данной цепи довольно сложный, поскольку она 3-х контурная
- 12. После замены Δ нагрузки на Y нагрузки получаем схему, которую рассматривали ранее со звездой. Её рассчитываем
- 14. Скачать презентацию









 Влажность воздуха
Влажность воздуха Физика твердой Земли. Геотермия
Физика твердой Земли. Геотермия Снежные причуды. Всё о снеге и снежинках
Снежные причуды. Всё о снеге и снежинках Источники света. Распространение света
Источники света. Распространение света Электрическое сопротивление
Электрическое сопротивление Международная система единиц СИ
Международная система единиц СИ Свободное падение тел
Свободное падение тел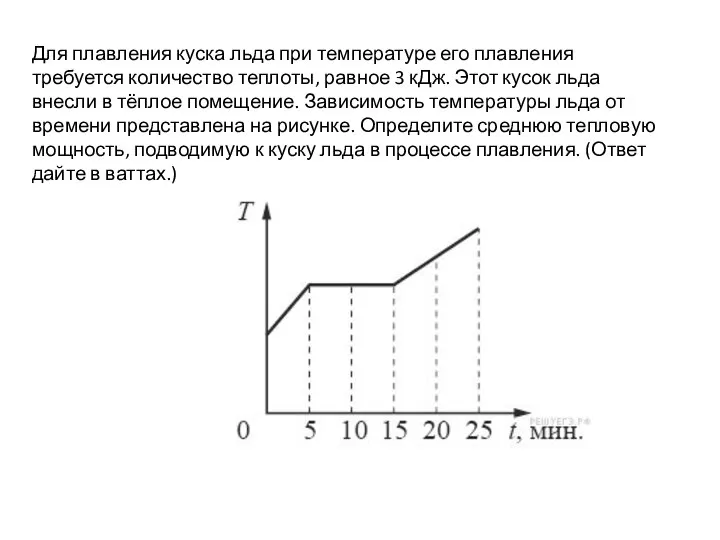 Определение тепловой мощности. ВПР, 9 класс
Определение тепловой мощности. ВПР, 9 класс Применение последовательного анализа и правила Вальда в задачах контроля
Применение последовательного анализа и правила Вальда в задачах контроля 13. СВЕТОТЕХНИКА 2020
13. СВЕТОТЕХНИКА 2020 Кинематика плоскопараллельного движения абсолютно твердого тела и сложного движения точки
Кинематика плоскопараллельного движения абсолютно твердого тела и сложного движения точки Качество обработанной поверхности
Качество обработанной поверхности Тепловое расширение тел
Тепловое расширение тел Что изучает физика?
Что изучает физика? Методика измерения массовой концентрации общего фосфора и фосфора фосфатов в пробах питьевых, природных и сточных вод
Методика измерения массовой концентрации общего фосфора и фосфора фосфатов в пробах питьевых, природных и сточных вод Радиоактивность и радиационно-опасные объекты
Радиоактивность и радиационно-опасные объекты Основы постановки научного эксперимента. ЯМР-спектроскопия. (Лекция 8)
Основы постановки научного эксперимента. ЯМР-спектроскопия. (Лекция 8) Введение в теплотехнику
Введение в теплотехнику Опыт Милликена. АФ1.4
Опыт Милликена. АФ1.4 Звуковые волны
Звуковые волны Кинематика точки
Кинематика точки Тезаурус
Тезаурус Волновые свойства света
Волновые свойства света Виды зубчатых передач
Виды зубчатых передач Мехатроника и мобильная робототехника
Мехатроника и мобильная робототехника Статистическая радиотехника. Узкополосный случайный процесс
Статистическая радиотехника. Узкополосный случайный процесс Методические указания к выполнению отчета по лабораторным работам
Методические указания к выполнению отчета по лабораторным работам ВКР: Разработка технологии ремонта форсунок дизельных двигателей автомобилей
ВКР: Разработка технологии ремонта форсунок дизельных двигателей автомобилей