Термодинамика однокомпонентных систем

Реальные газы. Летучесть
Уравнения для термодинамических потенциалов реальных газов можно получить на основании уравнений состояния. Однако в действительности не имеем уравнения состояния реального газа, которое описывало бы связь между параметрами состояния при любых условиях.
Единственным теоретически обоснованным уравнением для реальных газов является уравнение со вторым вириальным коэффициентом
pV = RT(1 + В/V), (9)
где
В = Во + α/Тn – β/Тm. (10)
Это уравнение выведено методами статистической механики и имеет большое теоретическое значение, но не представляет существенного практического интереса вследствие сложности определения B и правильности уравнения только при малых отклонениях от законов идеального газа.

Широко известно уравнение Ван-дер-Ваальса:
(р + а/V2)(V –b) = RT, (11)
которое характеризует не только изменения состояния газа, но и жидкости.
Постоянные a и b для каждого газа вычисляются из его критических параметров. Однако количественно это уравнение не всегда отвечает экспериментальным данным, а опытные значения a и b в обычных условиях примерно в два раза меньше рассчитанных. Уравнение также непригодно для высоких давлений.
Наиболее удовлетворительные результаты дает уравнение Битти – Бриджмена:
pV2 = RT [V + Во(1 – b/V)] /(1 – с/VT3) – Ао(1 – а/V), (12)
где a, b, c, A , B – эмпирические константы, характерные для каждого газа.

Гилберт Льюис предложил метод расчета термодинамических характеристик реальных газов, основанный на том, что для них формально сохраняются те же соотношения, что и для идеальных газов, но вместо давления вводится новая функция f – термодинамическая летучесть (или фугитивность), более кратко – летучесть.
Для изобарного потенциала постулируется для моля газа
G ≡ G(Т) + RTlnf. (13)
Дополнительно вводится условие, согласно которому по мере уменьшения давления величина летучести приближается к величине давления:
lim f/р → 1 при р → 0. (14)
Из (13) следует, что для изотермического процесса
ΔG = G2 – G1 = RTln(f2/f1). (15)
Значения f нужно найти для каждого реального газа при различных давлениях и температурах. Основой для вычисления летучести являются уравнения (13) и (14).

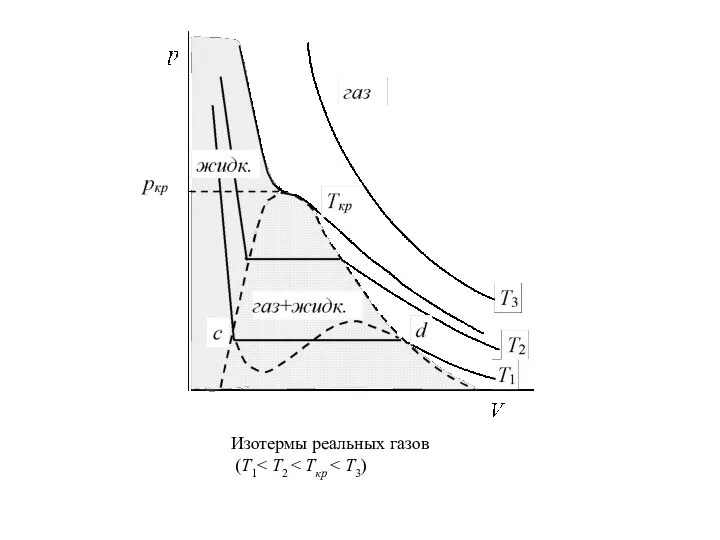
Изотермы реальных газов
(Т1< Т2 < Ткр < Т3)

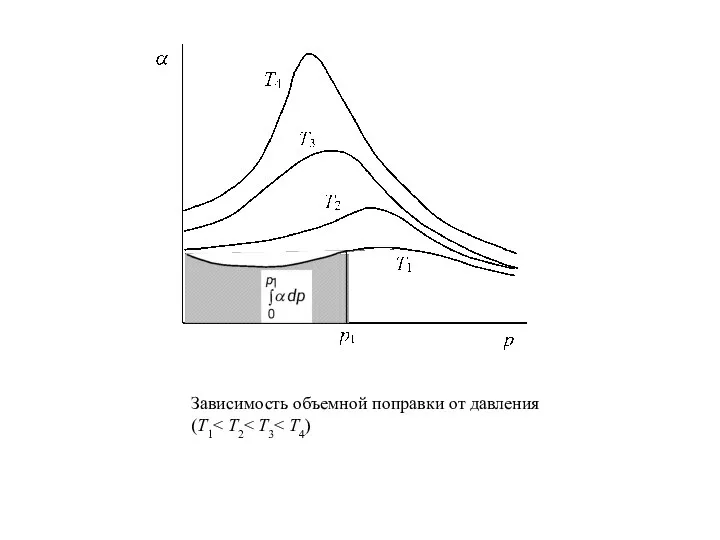
Зависимость объемной поправки от давления (Т1< Т2< Т3< Т4)

Стандартное состояние
Изобарный потенциал реального газа выражается уравнением (13), в котором G(T) – постоянная интегрирования, абсолютную величину которой определить невозможно.
Необходимо ввести некоторое стандартное состояние как начало отсчета G. Поскольку при р → 0 летучесть реального газа f → р, то за стандартное состояние можно было бы взять этот нижний уровень. Но такой выбор практически неудобен, так как при р → 0 изменение потенциала, по уравнению (15), ΔG → ∞.
Поэтому за стандартное состояние индивидуального газа при заданной температуре принимается гипотетическое состояние идеального газа, летучесть которого равняется единице, а энтальпия равняется энтальпии реального газа при этой же температуре и нулевом давлении. За единицу давления принимается 1 бар = 1,000.105 Па.

Переход газа из любого состояния в стандартное схематически изображен на рис.
Если реальный газ находится при данной температуре под давлением р (точка а), проведем изотермическое расширение до бесконечно малого давления (р → 0), а потом сжатие по изотерме идеального газа к р = 1 (точка о). Это и будет стандартное состояние, в котором f о = р = 1.
Для идеального газа всегда f = р и f o = 1 при любой температуре. Для реального газа при р = 1 его состояние мало отличается от стандартного, то есть можно считать, что практически эти состояния совпадают. Уравнение (13), с учетом стандартного состояния, можно записать:
G – Go(Т) = RTlnf/f o = RTlna. (26)
Отношения летучести в данном состоянии к f o называется активностью a = f/f o. Поскольку для газов f o =1, то для них f = а.

Переход в стандартное состояние
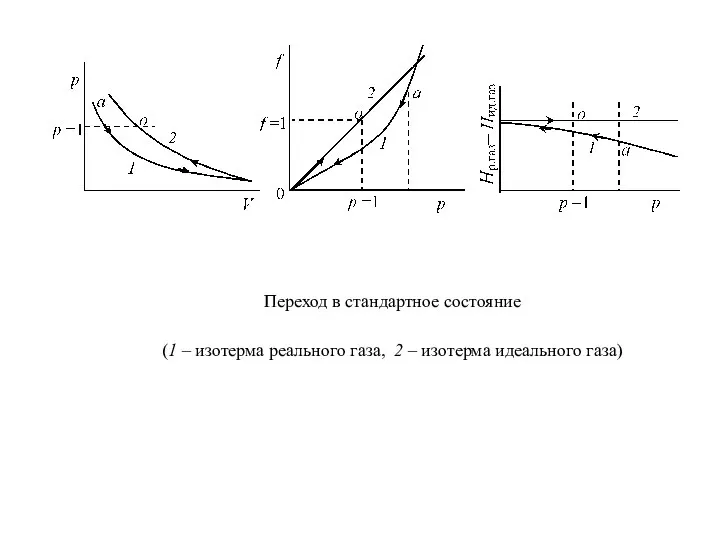
(1 – изотерма реального газа, 2 – изотерма идеального газа)

Фазовые превращения. Уравнение Клаузиуса – Клапейрона.
Индивидуальное вещество может находиться в газообразном, жидком или твердом (в различных кристаллических модификациях) состояниях. В равновесной системе, состоящей из нескольких фаз чистого вещества, возможны переходы из одной фазы в другую – плавление, испарение, сублимация, переход из одной кристаллической модификации в другую.
Эти процессы характеризуются определенным тепловым эффектом, скачкообразным изменением объема и энтропии при непрерывности изобарного потенциала. Их называют фазовыми переходами первого рода, или агрегатными превращениями.
Рассмотрим равновесный переход одного моля вещества из одной фазы 1 в другую 2 при постоянных давлении и температуре. В таком процессе производится только работа расширения и изменение внутренней энергии будет равно
U2 – U1 = Т(S2 – S1) – р(V2 – V1), (33)
или
U2 – TS2 + pV2 = U1 – TS1 + pV1. (34)

Более точным является правило Гильдебранда, согласно которому энтропии испарения жидкостей равны между собой при температурах, для которых мольные объемы насыщенного пара одинаковы. При этом изменение энтропии ΔS составляет 80 – 90 Дж моль–1.К при V = 49,5 л/моль.
Кроме рассмотренных, существуют также фазовые переходы второго рода, для которых характерно не только равенство изобарных потенциалов, но и равенство объемов и энтропий сосуществующих фаз:
ΔG = 0; ΔV = 0; ΔS = 0. (47)
Такие превращения не сопровождаются тепловым эффектом, но характеризуются изменением теплоемкости, коэффициента теплового расширения, сжимаемости.
К ним относятся переходы ферромагнитных тел в парамагнитные при температуре, называемой точкой Кюри, переходы металлов в сверхпроводящее состояние, превращение гелия I в гелий II и т.п.

Диаграммы состояния
Индивидуальное вещество может существовать в нескольких агрегатных состояниях, т. е. образовывать несколько фаз.
Например, вода, кроме жидкой и газообразной фаз, образует еще шесть модификаций льда, твердая сера имеет ромбическую и моноклиническую модификации и т.п.
Однако, максимальное число равновесно сосуществующих фаз обычно меньше общего числа возможных фаз. Это максимальное число можно определить по правилу фаз Гиббса :
f = k + 2 – s. (48)
Так как f максимально при s = 0, а k = 1, то максимальная величина f = 3, т.е. одновременно в однокомпонентной гетерогенной системе может находиться в равновесии не более трех фаз.

В общем случае нам не известны уравнения состояния отдельных фаз, поэтому зависимость между переменными, определяющими состояние системы, устанавливается при экспериментальном измерении температуры, давления и концентраций или объемов равновесных систем.
Эти данные используют для построения диаграмм состояния, которые являются графическим выражением этих зависимостей.
В случае однокомпонентной системы в уравнение состояния входит три переменных: температура T, давление p и концентрация c; или T, p и мольный объем V.
Для графического изображения связи между T, p и V необходимо использовать систему координат из трех взаимно перпендикулярных осей, каждая из которых соответствует одной из переменных. Любое состояние системы отображается в такой системе координат одной точкой, которая называется фигуративной точкой.

Совокупность этих точек дает диаграмму (рис.), состоящую из нескольких поверхностей, определенным образом расположенных в пространстве. Точки вне этих поверхностей не имеют физического смысла, так как любая фаза при заданных давлении и температуре имеет строго определенный объем, т.е. каждому сочетанию T и p соответствует единственно возможное значение V для данной фазы.
Исключением являются точки на поверхностях, соединяющих границы двух фазовых поверхностей. В этом случае фигуративная точка описывает средний мольный объем вещества во всей системе.
Подобные объемные диаграммы, позволяющие проследить за изменением всех переменных в уравнении состояния, называют полными диаграммами состояния.
Построение полных диаграмм трудоемко, а работать с ними неудобно, поэтому на практике обычно используют проекции полной диаграммы на одну из плоскостей, проходящих через оси координат.
Наиболее употребительными параметрами, определяющими условия существования системы, являются T и p, они хорошо поддаются измерению и регулированию. Поэтому чаще всего пользуются проекциями на плоскость T – p.

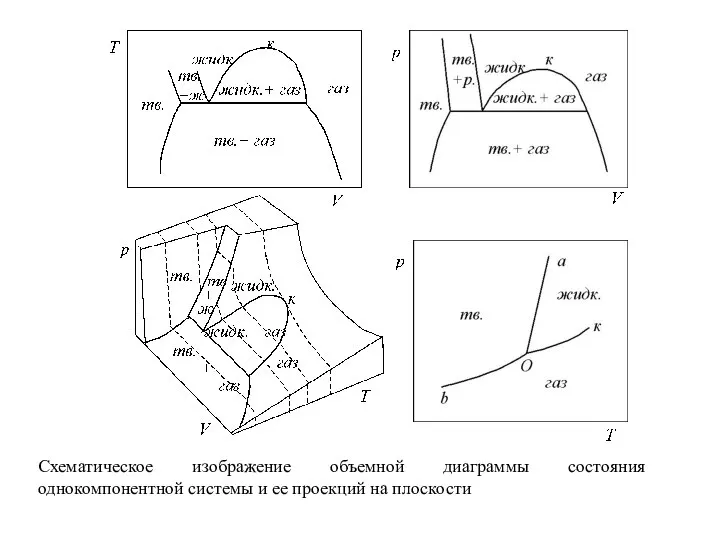
Схематическое изображение объемной диаграммы состояния
однокомпонентной системы и ее проекций на плоскости