Содержание
- 2. Тема 5.1.2 «Кинематика гармонических колебаний» ФГБОУ ВО СИБИРСКАЯ ПОЖАРНО-СПАСАТЕЛЬНАЯ АКАДЕМИЯ ГПС МЧС РОССИИ КОЛЕБАНИЯ в ПОЖАРНОМ
- 3. Учебные вопросы: Гармонические колебания и их характеристики. 2. Примеры гармонических колебаний. 3. Сложение гармонических колебаний. Тема
- 4. 1. Гармонические колебания и их характеристики Колебаниями называют движения или процессы, обладающие повторяемостью во времени. Колебания
- 5. Тема 5.1 «Кинематика гармонических колебаний» Колебания, возникающие за счет внешней, периодически меняющейся силы, называют вынужденными. Колебания,
- 6. Тема 5.1. «Кинематика гармонических колебаний» А – амплитуда колебания; ω - циклическая частота; (ωt + ϕ)
- 7. Тема 5.1. «Кинематика гармонических колебаний» Время одного полного колебания называется периодом: число полных колебаний в единицу
- 8. Тема 5.1 «Кинематика гармонических колебаний» Скорость и ускорение при гармонических колебаниях:
- 9. Тема 5.1 «Кинематика гармонических колебаний» Сила, действующая на колеблющуюся материальную точку массой m: Эта сила, независимо
- 10. Тема 5.1 «Кинематика гармонических колебаний» Уравнение движения для гармонических колебаний: Система, совершающая колебания, описываемые таким уравнением,
- 11. Тема 5.1 «Кинематика гармонических колебаний» Гармонические колебания изображают графически методом векторных диаграмм.
- 12. Тема 5.1 «Кинематика гармонических колебаний» Кинетическая энергия гармонических колебаний: Максимальное значение кинетической энергии:
- 13. Тема 5.1 «Кинематика гармонических колебаний» Потенциальная энергия гармонических колебаний равна работе упругой силы:
- 14. Тема 5.1. «Кинематика гармонических колебаний» Полная энергия колебаний равна: Полная энергия при гармонических колебаниях остается постоянной
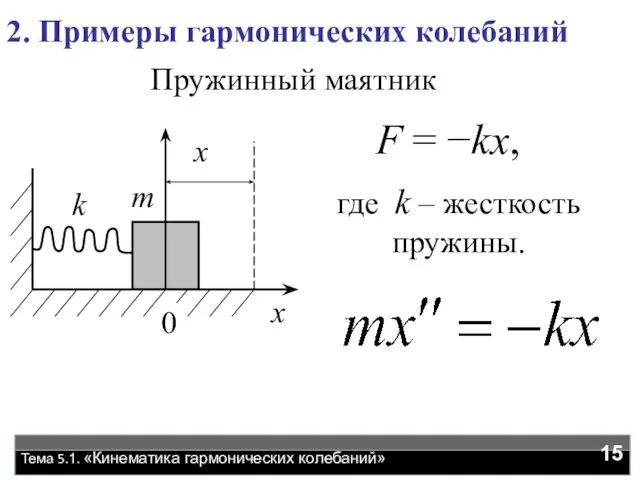
- 15. где k – жесткость пружины. F = −kx, Тема 5.1. «Кинематика гармонических колебаний» 2. Примеры гармонических
- 16. Тема 5.1 «Кинематика гармонических колебаний» Сопоставляя с уравнением (1), находим циклическую частоту и период колебаний пружинного
- 17. Тема 5.1 «Кинематика гармонических колебаний» Потенциальная энергия пружинного маятника:
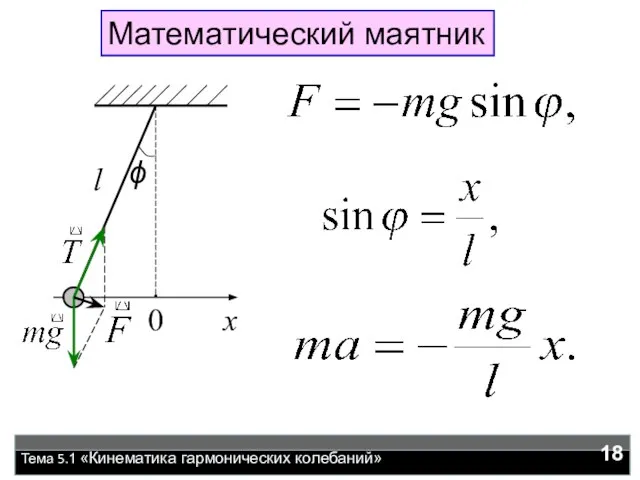
- 18. Тема 5.1 «Кинематика гармонических колебаний» Математический маятник
- 19. Тема 5.1 «Кинематика гармонических колебаний» Сопоставляя с уравнением (1), находим:
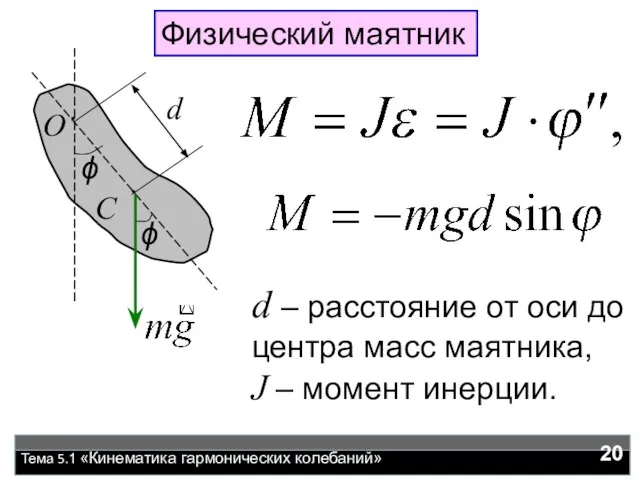
- 20. Тема 5.1 «Кинематика гармонических колебаний» Физический маятник d – расстояние от оси до центра масс маятника,
- 21. Тема 5.1 «Кинематика гармонических колебаний» При малых углах sinϕ ≈ ϕ
- 22. Тема 5.1 «Кинематика гармонических колебаний» Сравнивая с уравнением (1), находим:
- 23. Тема 5.1 «Кинематика гармонических колебаний» 3. Сложение гармонических колебаний Сложение колебаний одного направления и частоты
- 24. Тема 5.1 «Кинематика гармонических колебаний» уравнение результирующего колебания:
- 25. Тема 5.1 «Кинематика гармонических колебаний» Точка, участвуя в двух гармонических колебаниях одного направления и одинаковой частоты,
- 26. Тема 5.1 «Кинематика гармонических колебаний» Сложение взаимно перпендикулярных колебаний
- 27. Тема 5.1 «Кинематика гармонических колебаний» траектория результирующего колебания имеет форму эллипса.
- 28. Тогда sinα = 0 и cosα = 1, и эллипс вырождается в отрезок прямой: Тема 5.1.
- 29. Тема 5.1. «Кинематика гармонических колебаний» Амплитуда результирующего колебания: Прямая составляет с осью х угол:
- 30. Тема 5.1. «Кинематика гармонических колебаний» б) ( m = 0, ±1, ±2, …). В этом случае
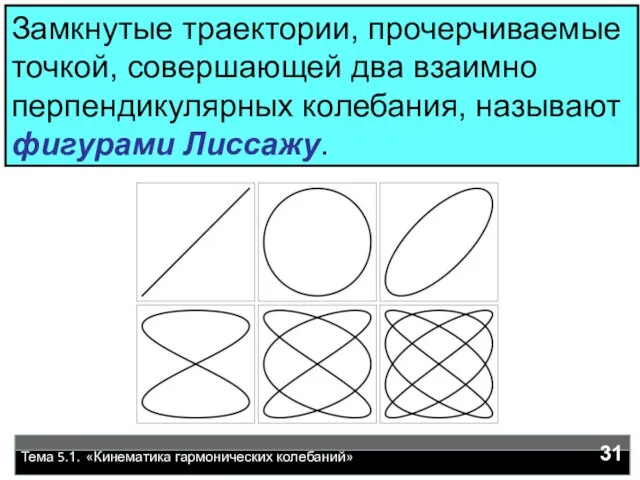
- 31. Тема 5.1. «Кинематика гармонических колебаний» Замкнутые траектории, прочерчиваемые точкой, совершающей два взаимно перпендикулярных колебания, называют фигурами
- 32. Итак, мы изучили следующие учебные вопросы: 1. Гармонические колебания и их характеристики. 2. Примеры гармонических колебаний.
- 34. Скачать презентацию



























 Презентация на тему Работа и мощность тока
Презентация на тему Работа и мощность тока  Техническая механика. Термины и определения
Техническая механика. Термины и определения Прямолинейное равномерное движение
Прямолинейное равномерное движение Магнитные цепи
Магнитные цепи Структура и оптические свойства наночастиц, полученных импульсной лазерной абляцией меди в газовой среде
Структура и оптические свойства наночастиц, полученных импульсной лазерной абляцией меди в газовой среде Важный раздел механики: Колебания и волны
Важный раздел механики: Колебания и волны Элементы машиноведения. Составные части машин
Элементы машиноведения. Составные части машин Электрические конденсаторы
Электрические конденсаторы Устройство микросамолёта R-20 Птенец-2
Устройство микросамолёта R-20 Птенец-2 Control of nonlinear dynamics of electromechanical systems
Control of nonlinear dynamics of electromechanical systems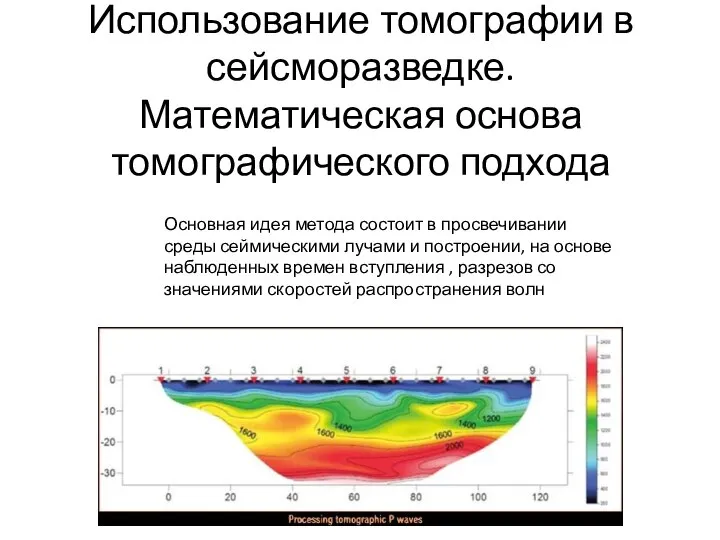 Использование томографии в сейсморазведке. Математическая основа томографического подхода
Использование томографии в сейсморазведке. Математическая основа томографического подхода Новая жизнь полной интегрируемости 2
Новая жизнь полной интегрируемости 2 Альтернативная энергетика
Альтернативная энергетика Определение параметров колебательного движения
Определение параметров колебательного движения ԱՎԱՐՏԱԿԱՆ ԱՇԽԱՏԱՆՔ ՄԱՍՆԱԳԻՏՈՒԹՅՈՒՆ` ՀԱՄԱԿԱՐԳՉԱՅԻՆ ԳԵՂԱՐՎԵՍՏԱԿԱՆ ՆԱԽԱԳԾՈՒՄ
ԱՎԱՐՏԱԿԱՆ ԱՇԽԱՏԱՆՔ ՄԱՍՆԱԳԻՏՈՒԹՅՈՒՆ` ՀԱՄԱԿԱՐԳՉԱՅԻՆ ԳԵՂԱՐՎԵՍՏԱԿԱՆ ՆԱԽԱԳԾՈՒՄ Колебания
Колебания Физические величины, используемые в химии
Физические величины, используемые в химии Графическое представление результатов измерений
Графическое представление результатов измерений Презентация на тему Постоянные магниты Магнитное поле Земли
Презентация на тему Постоянные магниты Магнитное поле Земли  Взаимодействие тел. Масса
Взаимодействие тел. Масса Презентация на тему Элементы квантовой физики для учителя
Презентация на тему Элементы квантовой физики для учителя  Презентация на тему Постоянный электрический ток
Презентация на тему Постоянный электрический ток  Ядерная бомба
Ядерная бомба Последовательное и параллельное соединение проводников
Последовательное и параллельное соединение проводников Изучение магнитооптической дифракции в пленках ферритов-гранатов
Изучение магнитооптической дифракции в пленках ферритов-гранатов Уравнения состояния идеального газа
Уравнения состояния идеального газа Звездный час
Звездный час Диагностика дизельных двигателей
Диагностика дизельных двигателей