Содержание
- 2. Теорема минимальной реализации схемы усилителя Минимальная реализация программируемого усилителя с управляемым сопротивлением Лекция 10 ПЛАН
- 3. Лекция 10 Программируемые операционные усилители (ОУ) применяются в электронных схемах, к которым предъявляются жесткие ограничения по
- 4. Лекция 10 Теорема минимальной реализации схемы усилителя Для минимальной реализации набора из N произвольных коэффициентов усиления
- 5. Лекция 10 Так как коэффициент усиления является безразмерной величиной, то как минимум два пассивных элемента одинаковой
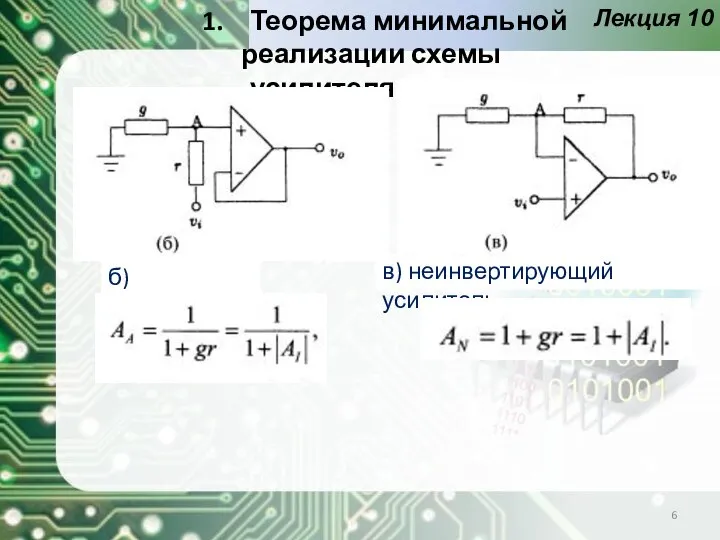
- 6. Лекция 10 Теорема минимальной реализации схемы усилителя б) аттенюатор в) неинвертирующий усилитель
- 7. Лекция 10 Из уравнений видно, что коэффициенты Ак ≤ 0, 0 ≤ Ак ≤ 1 или
- 8. Лекция 10 Пусть есть один ОУ и N ключей, работающих либо в режиме одиночного, либо группового
- 9. Лекция 10 Оба параметра g или r меняются одновременно. Если варьировать оба параметра независимо друг от
- 10. Лекция 10 Таким образом, коэффициентом усиления можно управлять изменением комбинации параметров g - r в схемах
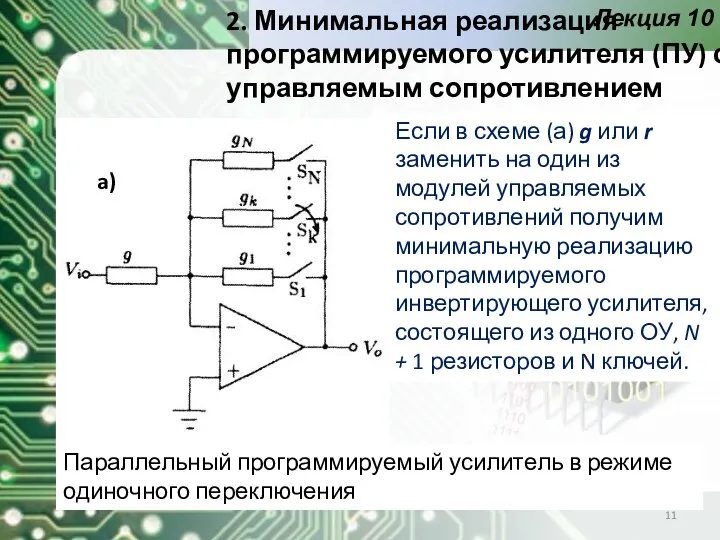
- 11. Лекция 10 2. Минимальная реализация программируемого усилителя (ПУ) с управляемым сопротивлением Параллельный программируемый усилитель в режиме
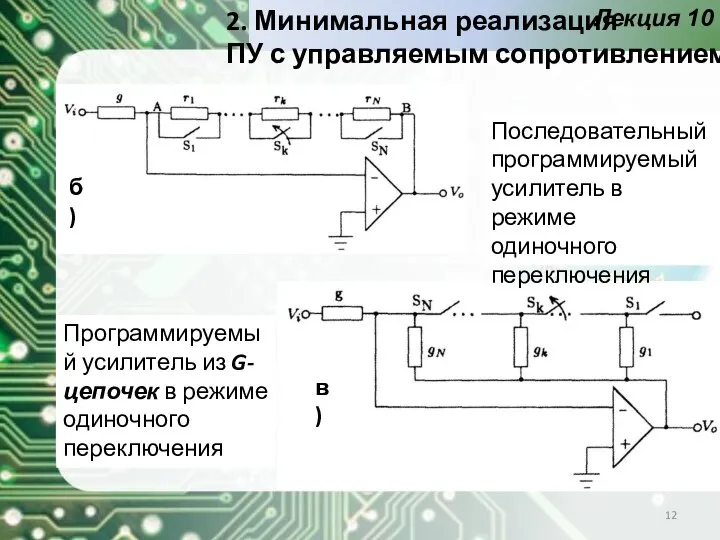
- 12. Лекция 10 2. Минимальная реализация ПУ с управляемым сопротивлением Последовательный программируемый усилитель в режиме одиночного переключения
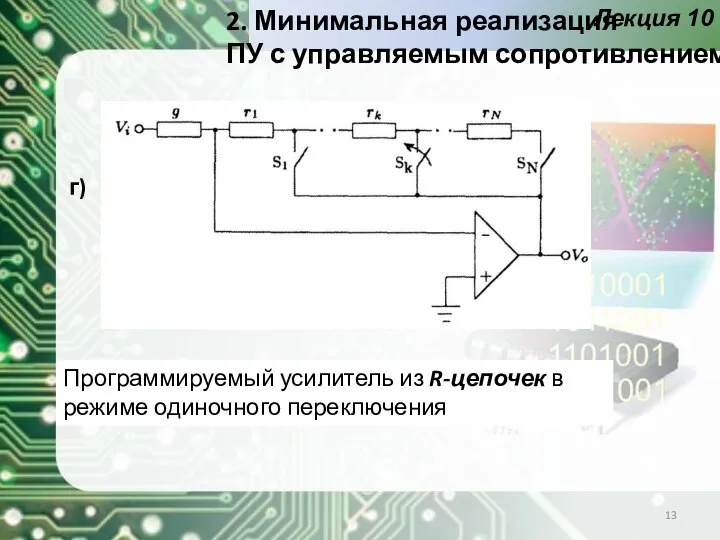
- 13. Лекция 10 Программируемый усилитель из R-цепочек в режиме одиночного переключения г) 2. Минимальная реализация ПУ с
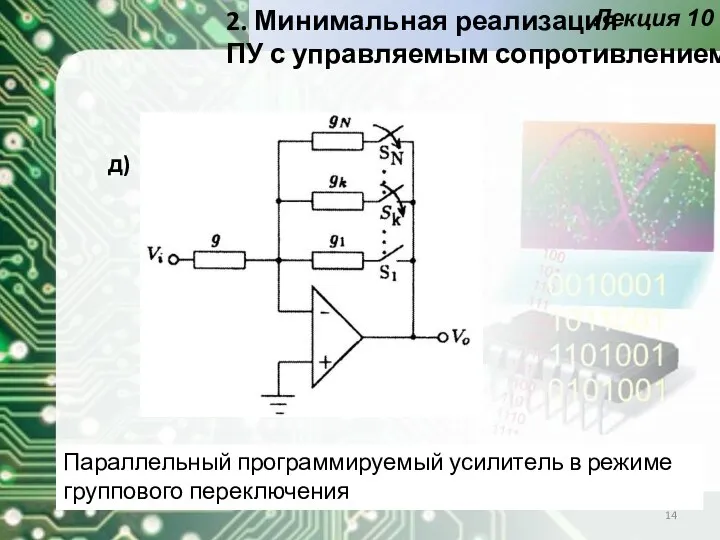
- 14. Лекция 10 Параллельный программируемый усилитель в режиме группового переключения 2. Минимальная реализация ПУ с управляемым сопротивлением
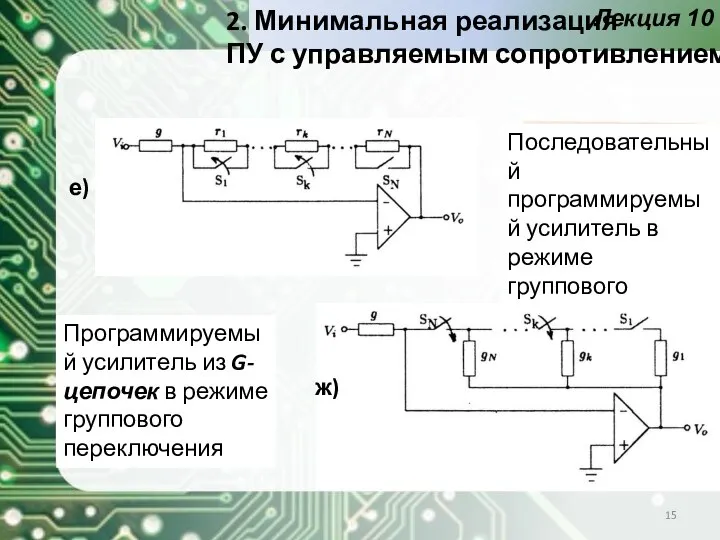
- 15. Лекция 10 2. Минимальная реализация ПУ с управляемым сопротивлением Последовательный программируемый усилитель в режиме группового переключения
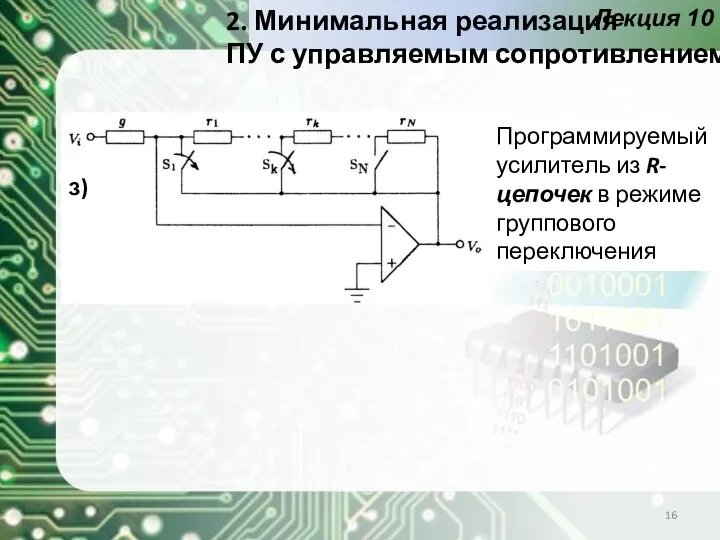
- 16. Лекция 10 Программируемый усилитель из R-цепочек в режиме группового переключения з) 2. Минимальная реализация ПУ с
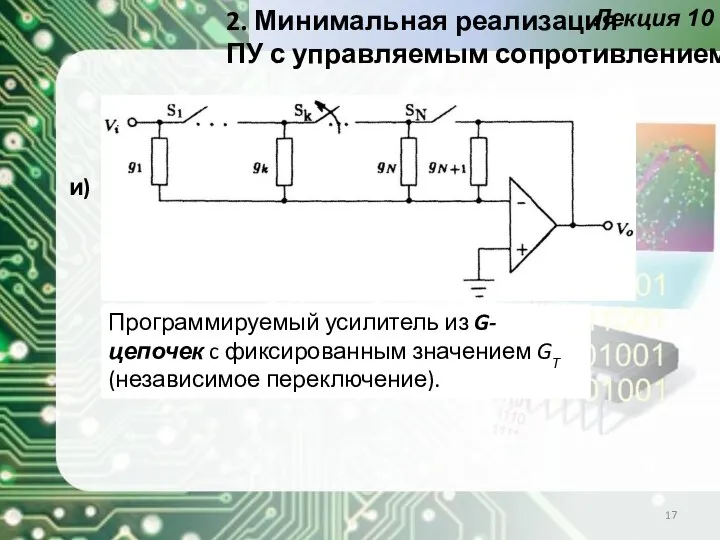
- 17. Лекция 10 и) 2. Минимальная реализация ПУ с управляемым сопротивлением Программируемый усилитель из G-цепочек c фиксированным
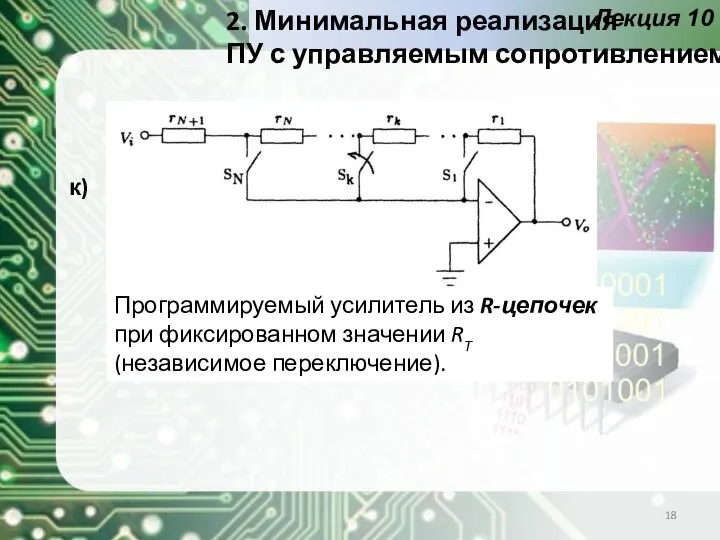
- 18. Лекция 10 Программируемый усилитель из R-цепочек при фиксированном значении RT (независимое переключение). к) 2. Минимальная реализация
- 19. Лекция 10 На рис. (а)-(з) показаны только варианты схем с фиксированным параметром g. Предполагается, что реализуется
- 20. Лекция 10 Задание для самостоятельной работы Разработайте схемы для получения наборов сопротивлений: а) 0, 1, 2,
- 21. Лекция 10 Проверь себя! Вопрос 1: … Ответы: а) действующее значение напряжения б) мгновенное в) среднее
- 22. Лекция 10 Проверь себя! Вопрос 2: … Ответы: а) действующее значение напряжения б) мгновенное в) среднее
- 23. Лекция 10 Проверь себя! Вопрос 3 : … Ответы: а)
- 24. Лекция 10 Проверь себя! Вопрос 4 : … Ответы: а)
- 25. Лекция 10 Проверь себя! Вопрос 5 : … Ответы: а) б) в) г) д)
- 27. Скачать презентацию












 printsip_raboty_DVS_Demin
printsip_raboty_DVS_Demin Условия плавания тел
Условия плавания тел Российский истребитель СУ-47 (С-37) Беркут
Российский истребитель СУ-47 (С-37) Беркут Оптическое излучение
Оптическое излучение Проектирование компрессорных установок горных предприятий. Занятие 7
Проектирование компрессорных установок горных предприятий. Занятие 7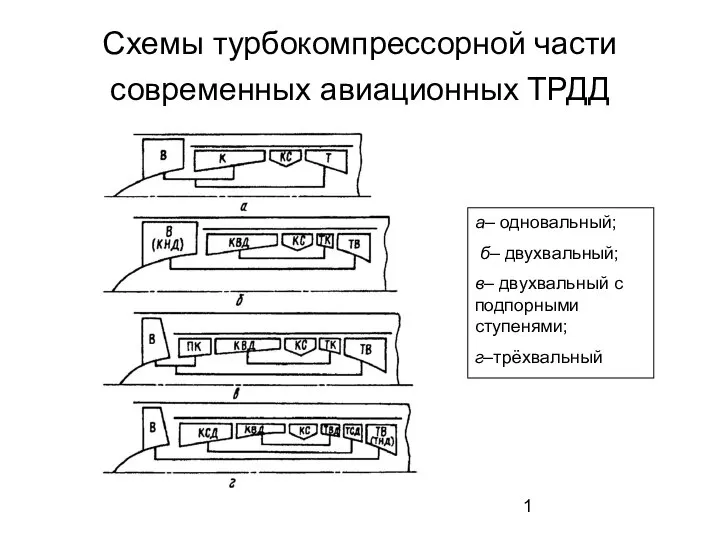 Конвертированные двигатели. Схемы турбокомпрессорной части современных авиационных ТРДД
Конвертированные двигатели. Схемы турбокомпрессорной части современных авиационных ТРДД Отчёт по практикуму по экспериментальной физике. Лабораторная работа Coulomb Blockade Thermometer
Отчёт по практикуму по экспериментальной физике. Лабораторная работа Coulomb Blockade Thermometer Механическое движение
Механическое движение Тренажер формул по физике Постоянный электрический ток
Тренажер формул по физике Постоянный электрический ток Рентгеновская астрономия
Рентгеновская астрономия Элементы ядерной физики. Лекция16
Элементы ядерной физики. Лекция16 Электростатическое поле в диэлектриках. Лекция № 2
Электростатическое поле в диэлектриках. Лекция № 2 Философский образ науки и техники
Философский образ науки и техники PITSTOP_05 Project Summary
PITSTOP_05 Project Summary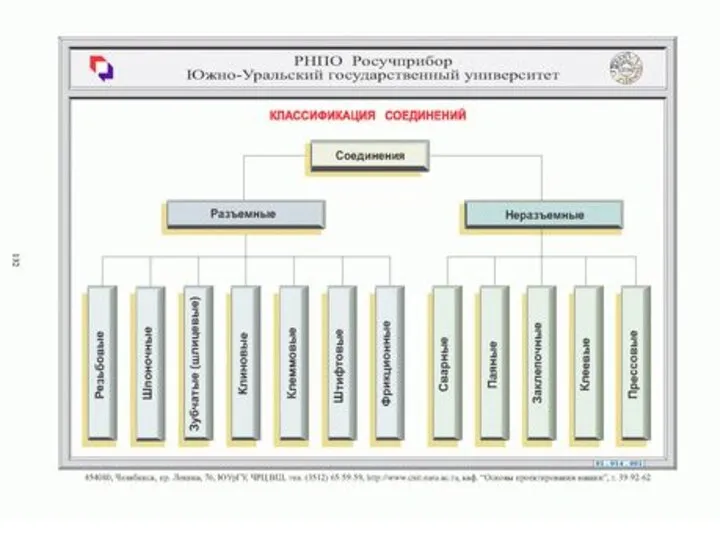 Классаификация соединений
Классаификация соединений Система. Объекты
Система. Объекты Уравнения и диапазоны. Лекция 2
Уравнения и диапазоны. Лекция 2 Сила тока. Измерение силы тока
Сила тока. Измерение силы тока Электрический ток в растворах и расплавах электролитов
Электрический ток в растворах и расплавах электролитов Зубчатые передачи
Зубчатые передачи Новые вспенинные и волокнистые композиционные материалы
Новые вспенинные и волокнистые композиционные материалы Особенности распространения и восприятия света
Особенности распространения и восприятия света Презентация по физике "Числовой луч" -
Презентация по физике "Числовой луч" -  Матрицы и действия над ними
Матрицы и действия над ними Они были первыми
Они были первыми Механические колебания. Физика. 9 класс
Механические колебания. Физика. 9 класс Перемещение при прямолинейном равноускоренном движении. Урок 1
Перемещение при прямолинейном равноускоренном движении. Урок 1 Полезные свойства кавитации
Полезные свойства кавитации