Гидростатическое давление в точке. Тема 1

В результате действия поверхностных и массовых сил внутри жидкости возникает напряжение сжатия, называемое гидростатическим давлением.

Единицы измерения и виды гидростатического давления
Виды гидростатического давления:
Полное (абсолютное) Pабс – величина давления, отсчитываемая от «0» (с учетом атмосферного);
Атмосферное давление Pa – давление, создаваемое окружающей воздушной средой (Pa = 105 Па);
Избыточное давление Pизб – превышение давления над атмосферным (отсчитывается от атмосферного): Pизб = Pабс – Pa = ρgh;
Вакуумметрическое (отрицательное избыточное) Pвак – недостаток давления до атмосферного: Pвак = Pa – P.

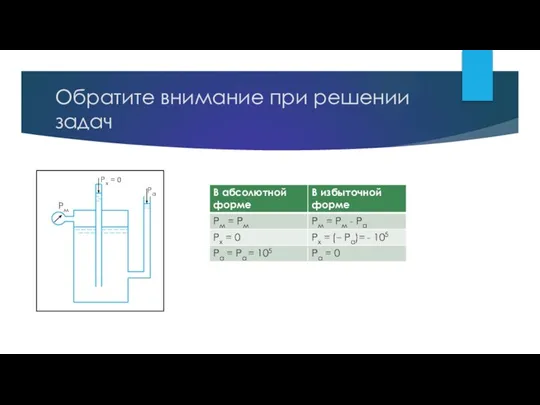
Обратите внимание при решении задач

P = Pх + ρgh
P – давление в точке;
Pх – давление на поверхности жидкости;
ρgh – избыточное давление, создаваемое слоем вышележащей жидкости.
– это поверхность, во всех точках которой давление одинаково.
Условия равного давления:
точки должны располагаться в одной горизонтальной плоскости;
точки должны располагаться в жидкости одного и того же вида.

Задача
В закрытом резервуаре имеется вода (h1 = 30 см) и масло (h2 = 50 см), плотность масла ρм = 800 кг/м3. Найти давление Рх на поверхности масла, если показания ртутного прибора h3 = 40 см.
1. Обозначаем 2 точки на поверхности равного давления.
2. Записываем основное уравнение гидростатики для каждой точки:
Р1 = Pa
P2 = Px + g(ρмh2 + ρвh1 + ρртh3)
Pa = Px + g(ρмh2 + ρвh1 + ρртh3)
3. Выражаем Px:
Px = Pa - g(ρмh2 + ρвh1 + ρртh3) = 105 – 9,81(800 ∙ 0,5 + 1000 ∙ 0,3 + 13600 ∙ 0,4) = 39828 Па = 39,83 кПа

Тема 2.
Сила гидростатического давления на плоские поверхности
МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное учреждение высшего образования
Санкт-Петербургский государственный архитектурно-строительный университет

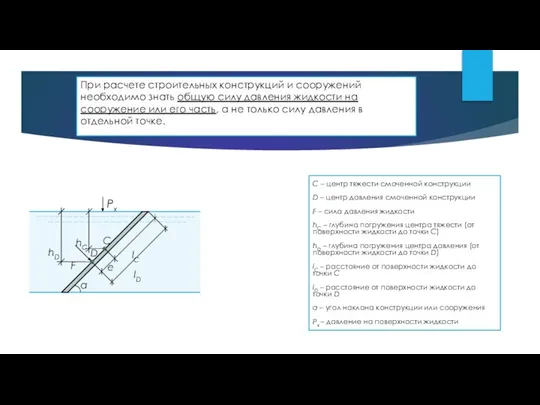
При расчете строительных конструкций и сооружений необходимо знать общую силу давления жидкости на сооружение или его часть, а не только силу давления в отдельной точке.
C – центр тяжести смоченной конструкции
D – центр давления смоченной конструкции
F – сила давления жидкости
hC – глубина погружения центра тяжести (от поверхности жидкости до точки С)
hD – глубина погружения центра давления (от поверхности жидкости до точки D)
lC – расстояние от поверхности жидкости до точки C
lD – расстояние от поверхности жидкости до точки D
α – угол наклона конструкции или сооружения
Pх – давление на поверхности жидкости

Определение величины силы гидростатического давления
Силой давления (F) называется равнодействующая элементарных сил гидростатического давления (PC) на некоторую поверхность (S).
* Обычно для таких расчетов учитывается только величина избыточного давления (Pизб), так как атмосферное давление действует равномерно со всех сторон конструкции и само себя уравнивает.
F = PC ∙ S [Н]
При Px = Pизб:
F = (Pизб + ρghC ) ∙ S
При Px = Pа:
F = ρghC ∙ S
PC – величина давления в точке С, [Па]
S – площадь конструкции, на которую действует жидкость [м2]
Px – давление на поверхности жидкости, [Па]
ρghC – избыточное давление, создаваемое слоем вышележащей жидкости, [Па]
hC – глубина погружения центра тяжести, [м] (см. табл. или считать)

Определение координат точки приложения силы давления (координат точки D)
Сила F прикладывается в точке D, называемой центром давления, перпендикулярно к поверхности.
Центр давления D всегда ниже центра тяжести C на величину, равную эксцентриситету e.
Для вертикальных стенок
hC = lC ; hD = lD
e
Для наклонных стенок
e
e

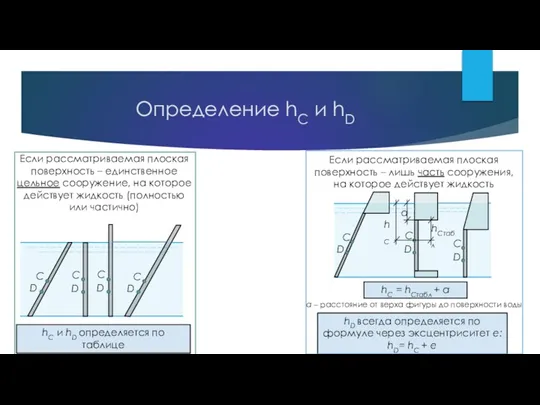
Определение hC и hD
Если рассматриваемая плоская поверхность – лишь часть сооружения, на которое действует жидкость
hC = hCтабл + a
а
hC
hCтабл
a – расстояние от верха фигуры до поверхности воды
hD всегда определяется по формуле через эксцентриситет e:
hD= hC + е

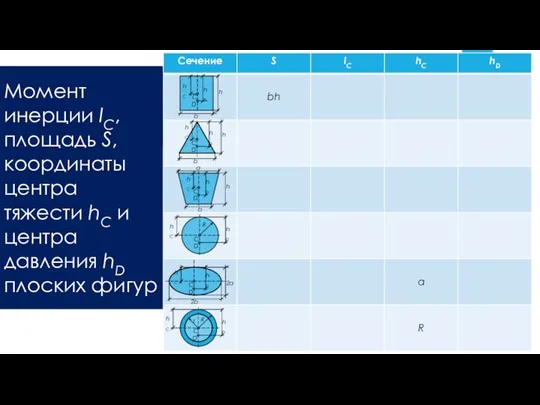
Момент инерции IC, площадь S, координаты центра тяжести hC и центра давления hD плоских фигур
b
h
hC
hD
C
D
b
C
D
hC
h
hD
a
h
C
D
C
D
hC
hD
R
C
D
2a
C
D
R
hC
hD
r

Для решения задач на данную тему используются:

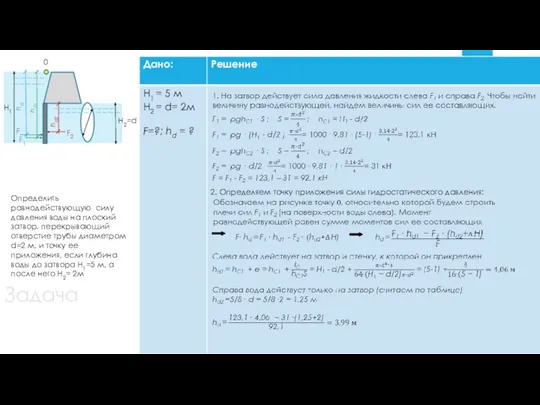
Задача
Определить равнодействующую силу давления воды на плоский затвор, перекрывающий отверстие трубы диаметром d=2 м, и точку ее приложения, если глубина воды до затвора H1=5 м, а после него H2= 2м
2. Определяем точку приложения силы гидростатического давления:
F1
F2
hd1
hd2
F
hd
0

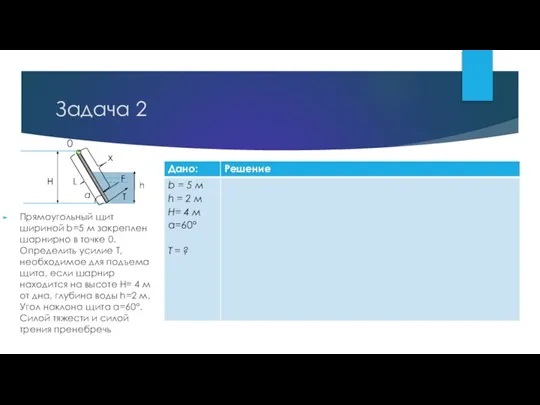
Задача 2
Прямоугольный щит шириной b=5 м закреплен шарнирно в точке 0. Определить усилие Т, необходимое для подъема щита, если шарнир находится на высоте H= 4 м от дна, глубина воды h=2 м. Угол наклона щита α=60°. Силой тяжести и силой трения пренебречь
x
L
h
F
T
H
0
α

Тема 3.
Сила гидростатического давления на криволинейные поверхности
МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное учреждение высшего образования
Санкт-Петербургский государственный архитектурно-строительный университет

При определении силы давления F на криволинейные поверхности неизвестна не только точка приложения силы, но и ее направление (в отличие от плоских поверхностей), так как в каждой точке направление силы нормально поверхности.
F
Общие положения

Необходимо определить составляющие силы F:
** Если образующая цилиндрической поверхности описывает окружность, то сила F пройдет через центр окружности (точка 0 на рисунке)
Сила давления на цилиндрические поверхности

Горизонтальная составляющая силы (Fx)
Горизонтальная составляющая силы давления на цилиндрическую поверхность равна силе давления на ее вертикальную проекцию

Вертикальная составляющая силы (Fz)
Вертикальная составляющая силы давления на цилиндрическую поверхность равна весу жидкости (γ = ρg) в объеме тела давления V.
Sт.д. – площадь тела давления (Sт.д. = ABC или A’B’C’)
b – ширина тела давления (b = AA’, или BB’, или СС’)
Fz

Определение объема тела давления
Объем тела давления представляет собой объем, ограниченный цилиндрической поверхностью, ее проекцией на поверхность жидкости или ее продолжение, а также вертикальными поверхностями, соединяющими границы цилиндрической поверхности с соответствующими точками ее проекции.
Тело давления положительное, если объем заполнен жидкостью
Fz
Fz = Fтяж
и совпадает по направлению
Тело давления отрицательное (мнимое), если объем не заполнен жидкостью
Fz = Fтяж ,
но противоположна по направлению

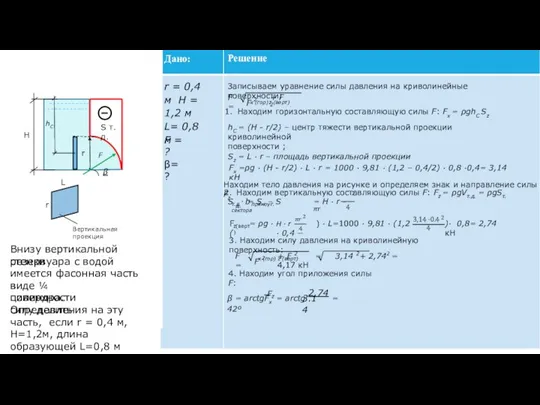
Дано:
Решение
r = 0,4 м H = 1,2 м L= 0,8 м
F = ?
β= ?
Записываем уравнение силы давления на криволинейные поверхности:
F =
F 2
+ F 2
x (гор) z (верт).
Н
r
S т.д.
Вертикальная проекция
r
L
hC
Находим горизонтальную составляющую силы F: Fx = ρghC Sz
hC = (H - r/2) – центр тяжести вертикальной проекции криволинейной
поверхности ;
Sz = L ∙ r – площадь вертикальной проекции
Fx =ρg ∙ (H - r/2) ∙ L ∙ r = 1000 ∙ 9,81 ∙ (1,2 – 0,4/2) ∙ 0,8 ∙0,4= 3,14 кН
Находим вертикальную составляющую силы F: Fz = ρgVт.д. = ρgSт.д.∙ b
Находим тело давления на рисунке и определяем знак и направление силы Fz
S = S – S
т.д. прямоуг. сектора
2
= H ∙ r - ??
4
z(верт)
F = ρg ·(
??
2
4
H ∙ r - ) · L=1000 · 9,81 · (1,2 ∙ 0,4 −
3,14 ·0.4
2
4
)· 0,8= 2,74 кН
3. Находим силу давления на криволинейную поверхность:
F =
F 2
x (гор) z (верт)
+ F 2 = 3,14 2+ 2,742 = 4,17 кН
4. Находим угол приложения силы F:
Fx
3.14
β = arctg Fz = arctg 2,74 = 42º
β
Внизу вертикальной стенки
резервуара с водой
имеется фасонная часть в
виде ¼ поверхности
цилиндра. Определить
силу давления на эту часть, если r = 0,4 м, H=1,2м, длина образующей L=0,8 м
F

Тема 5.
Уравнение Бернулли для вязкой (реальной) жидкости
МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное учреждение высшего образования
Санкт-Петербургский государственный архитектурно-строительный университет

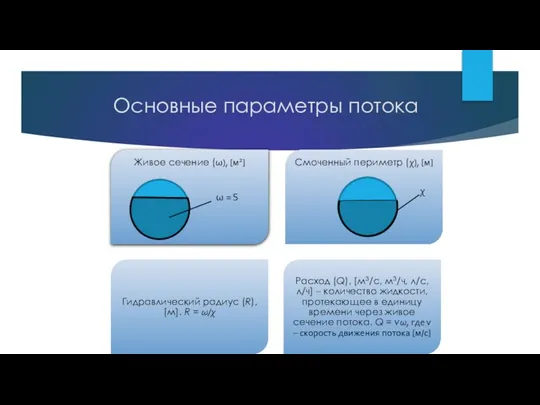
Основные параметры потока
ω = S
χ

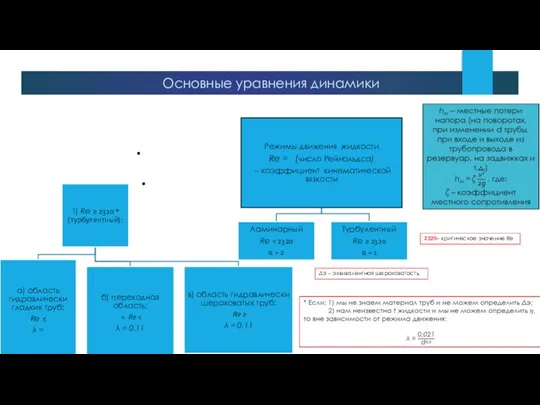
Основные уравнения динамики

Δэ – эквивалентная шероховатость.
Основные уравнения динамики
2320– критическое значение Re

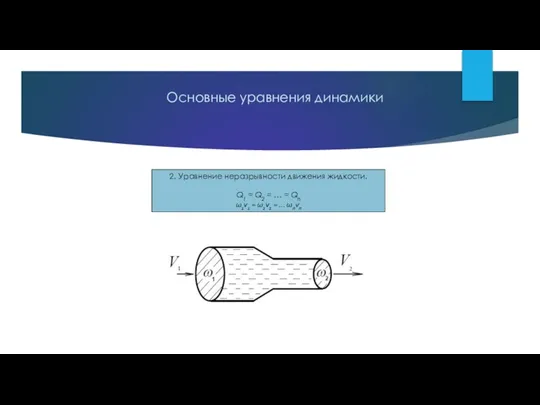
2. Уравнение неразрывности движения жидкости.
Q1 = Q2 = … = Qn
ω1v1 = ω2v2 = … ωnvn
Основные уравнения динамики

Задача
1. Отмечаем на рисунке сечения I-I (на поверхности жидкости в баке) и II-II (на конце трубопровода).
Определить напор в резервуаре Н и расход воды Q (t = 15ºC), протекающий по трубопроводу из чугуна, имеющего переменное сечение: d1 = 100 мм, d2 = 120 мм, Общая длина трубопровода l2 = 100 м. Длина участка меньшего диаметра l1 = 70 м, причем на расстоянии l0 = 30 м от начала участка трубопровода имеется задвижка, наполовину закрытая. Скорость потока на выходе из трубы v2 = 1 м/с.
l0
l1
l2
d1
d2
H
2. Отмечаем на рисунке горизонтальную ось сравнения (по оси трубопровода).
3. Записываем уравнение Бернулли для выбранных сечений:
zI = H;
zII = 0;
PII = 0;
∑h = hвх + hl0 + hзад + h(l1-l0) +hрасш + h(l2-l1)
4. Переписываем уравнение Бернулли с найденными значениями:
5. Далее определяем число Рейнольдса для каждого участка трубопровода: Re1 и Re2:
Из условия неразрывности жидкости: Q = ω1v1 = ω2v2
Теперь находим Re1 и Re2:
6. Определяем области труб, чтобы посчитать коэффициент Дарси (λ):
7. Исходя из найденной области труб, определяем коэффициент Дарси:

Задача
Определить расход воды Q (t = 15ºC), протекающий по трубопроводу из чугуна, имеющего переменное сечение: d1 = 100 мм, d2 = 120 мм. Общая длина трубопровода l2 = 100 м. Длина участка меньшего диаметра l1 = 70 м, причем на расстоянии l0 = 30 м от начала участка трубопровода имеется задвижка, наполовину закрытая. Скорость потока на выходе из трубы v2 = 1 м/с. Построить напорную и пьезометрическую линии и определить напор в резервуаре H.
l0
l1
l2
d1
d2
H
9. Определяем потери напора:
10. Считаем значения напора H:
8. Считаем значения скоростного напора:

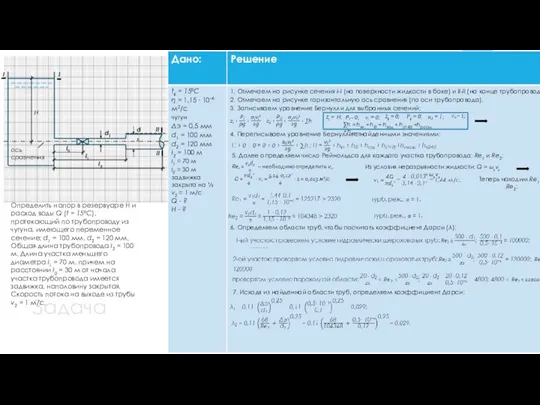
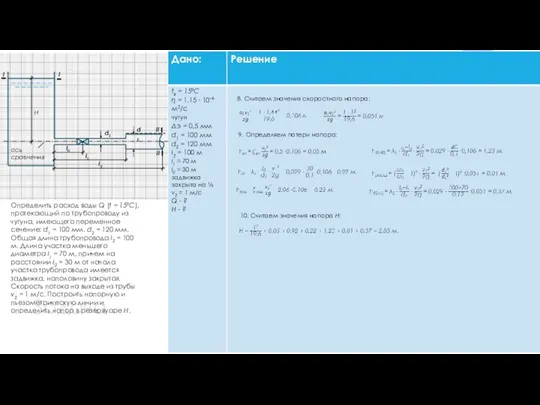
Задача 2
d2
d1
H
h
Po
А
В
l1
l2
Резервуары А и В соединены горизонтальной новой чугунной трубой переменного сечения: l1=10 м, d1=50 мм, l2= 6 м, d2=100 мм. Напор воды в резервуаре А при t0в =15 ℃ Н=8 м. Определить расход воды в трубопроводе, если манометрическое давление Р0=0,2 МПа и h=2 м.
чугун
Δэ = 0,5 мм
l1 = 10 м
d1 = 50 мм
l2 = 6 м
d2 = 100 мм
tв = 15ºC
η = 1,15 ∙ 10-6 м2/с
H = 8 м
h = 2 м
Р0 = 0,2 МПа
Q - ?

d2
d1
H
h
Po
Резервуары А и В соединены горизонтальной новой чугунной трубой переменного сечения: l1=10 м, d1=50 мм, l2= 6 м, d2=100 мм. Напор воды в резервуаре А при t0в =15 ℃ Н=8 м. Определить расход воды в трубопроводе, если манометрическое давление Р0=0,2 Мпа и h=2 м.
А
В
l1
l2

d2
d1
H
h
Po
Резервуары А и В соединены горизонтальной новой чугунной трубой переменного сечения: l1=10 м, d1=50 мм, l2= 6 м, d2=100 мм. Напор воды в резервуаре А при t0в =15 ℃ Н=8 м. Определить расход воды в трубопроводе, если манометрическое давление Р0=0,2 Мпа и h=2 м.
А
В
l1
l2

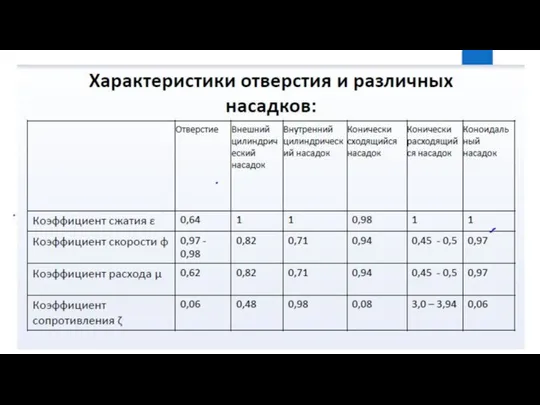
Тема 6.
Истечение жидкости через отверстия и насадки
МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное учреждение высшего образования
Санкт-Петербургский государственный архитектурно-строительный университет

Основные понятия
В разделе рассматриваются случаи малых отверстий и тонкой стенки

Насадки

1. Скорость истечения
* Если истечение происходит не в газ, а в другую жидкость, то:
H = H1 – H2

2. Расход жидкости через отверстие или насадок.
3. Скорость опорожнения

Типы задач

Задача
Исходя из того, что движение установившееся, следует: Q = Q1 + Q2 и Q0 = Q2.
Q0 = Q2: распишем, чему равняется Q0 = Q2.
Резервуар разделен тонкой стенкой, в которой имеется круглое отверстие диаметром d0 = 30 мм. Диаметр конически сходящегося насадка, через который вытекает вода из первого отсека d1 = 15 мм; диаметр внешнего цилиндрического насадка, через который вытекает вода из второго отсека d2 = 20 мм. Определить расход воды из бака Q и глубину H2 во втором отсеке, если глубина воды в первом отсеке H1 =1,25 м, а расстояние от дна до центра цилиндрического насадка h = 0,2м. Движение воды в резервуаре установившееся.
h
Q1
Q2
Q0
Считаем, чему равняется Q: Q = Q1 + Q2 = 0,82 +1 = 1,82 л/с.

H
d
D
В вертикальный цилиндрический сосуд диаметром D=1 м поступает вода из крана с расходом Q, которая затем вытекает через малое отверстие в дне сосуда при глубине воды в нем Н=1,5 м. Определить расход Q и диаметр отверстия, если после закрытия крана сосуд опорожняется за 19 минут
Дано:
Решение
D= 1 м H = 1,5 м
tоп = 19 мин
Q = ?
d=?
Время опорожнения сосуда при переменном напоре в 2 раза больше времени наполнения того же сосуда при постоянном напоре, т.е.
оп
?
? = 2? , где W – начальный объем воды в сосуде. Сосуд имеет
форму цилиндра W=
?D2
4
⋅ ?
? = =
2? ∙ ?2 ∙ ? 3,14 ∙ 12 ∙ 1,5
4 ∙ ?оп 2 ∙ 19 ∙ 60
= 0,039 м3/с = 39 л/с
Диаметр отверстия найдем из уравнения расхода жидкости,
вытекающей из отверстия:
? = ? ? 2 ?? = ? ∙
?d2
4
2 ??
? =
4?
?? 2 ??
=
4∙0,039
0,62∙3,14 19,6∙1,5
= 0,015 м = 15 мм

Тема 7.
Напорное движение в трубопроводах
МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное учреждение высшего образования
Санкт-Петербургский государственный архитектурно-строительный университет

Классификация трубопроводов
Классификация трубопроводов

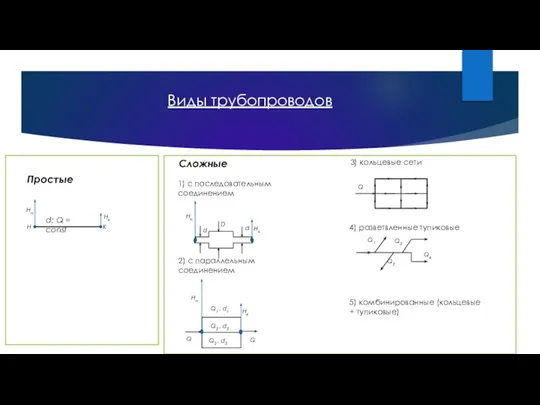
Длинные трубопроводы
Виды трубопроводов
Простые
Сложные
1) с последовательным соединением
2) с параллельным соединением
3) кольцевые сети
4) разветвленные тупиковые
5) комбинированные (кольцевые + тупиковые)

Длинные трубопроводы: расход
Для сетей главными являются две характеристики:
расход Q и напор Н.
а) узловой (сосредоточенный) – Qn – это расход, отделяющийся или присоединяющийся в конкретной точке сети.
Виды расходов
б) путевой (распределительный) – Qпут – это расход, отбираемый из трубопровода непрерывно: Qпут = q0 ∙ l, где: q0 – удельный путевой расход.
в) транзитный – это часть расхода трубопровода, предназначенная для снабжения жидкостью последующих участков сети.
Q3 – узловой расход для участка 2-3 и транзитный для участка 1-2.
г) расчетный – тот, по которому ведется гидравлический расчет:
если путевой расход находится на рассматриваемом участке, а после него есть еще расходы, расчетный расход будет находиться как сумма расходов после рассматриваемого участка + путевой расход на этом участке, определяемый по формуле 0,55 ∙ q0 ∙ l.
если путевой расход находится на рассматриваемом участке, а после него нет расходов, то расчетным расходом будет путевой расход на этом участке, определяемый по формуле 0,58 ∙ q0 ∙ l.
Qрасч1-2 = Q2 + Q3 + q02-3 ∙l2-3 + 0,55 ∙ q01-2 ∙ l1-2.
Qрасч1-2 = 0,58 ∙ q01-2 ∙ l1-2.

Длинные трубопроводы: напор
Определение потерь напора по длине hl:
! При параллельном соединении потери на пора на линиях равны