Слайд 2Эпиграф
Постоянные колебания приличны
только маятнику
Козьма Прутков

Слайд 3Малые гармонические колебания

Слайд 4Малые гармонические колебания

Слайд 5Малые гармонические колебания

Слайд 6Малые гармонические колебания

Слайд 7Малые гармонические колебания

Слайд 8Малые гармонические колебания

Слайд 9Малые гармонические колебания

Слайд 11Пример1 – Две пружины
Рассмотрим колебания груза массой m подвешенного к двум пружинам,

соединенным: а) последовательно, б) параллельно. Нашей задачей будет определение частоты колебаний груза, если коэффициенты жесткости пружин равны k1 и k2.
Слайд 18Пример 2 – Математический маятник
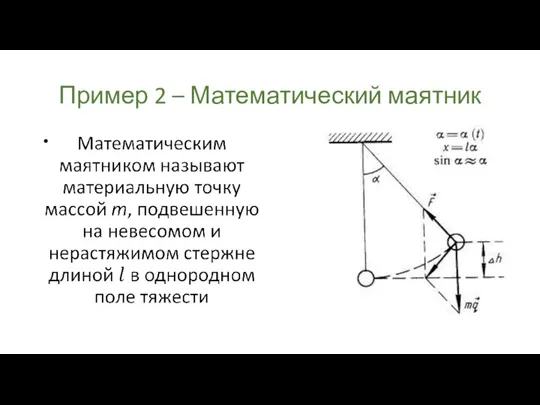
Слайд 19Пример 2 – Математический маятник

Слайд 20Пример 2 – Математический маятник

Слайд 21Пример 2 – Математический маятник

Слайд 22Пример 3 –Задача двух тел
Рассмотрим колебания, которые возникают в системе двух тел

разной массы m и M, связанных пружиной жесткости k после столкновения с частицей массы m, двигающейся со скоростью v. Удар будем считать лобовым и абсолютно упругим.
Слайд 28Пример 4 – Колебания ареометра
Ареометр массой m с цилиндрической трубкой диаметром d

плавает в жидкости плотностью ρ и приводится толчком в вертикальном направлении в движение Найдем частоту малых колебаний ареометра. Движение жидкости и ее сопротивление движению ареометра учитывать не будем.
Слайд 42Задача
Период затухающих колебаний Т = 1 с, логарифмический декремент затухания θ =

0,3, начальная фаза равна нулю. Смещение точки при t = 2T составляет 5 см. Запишите уравнение движения этого колебания
Слайд 44Вынужденные колебания - Резонанс

Слайд 45Вынужденные колебания - Резонанс

Слайд 46Вынужденные колебания - Резонанс

Слайд 47Вынужденные колебания - Резонанс
Зависимость амплитуды установившихся колебаний x от частоты вынужденной силы
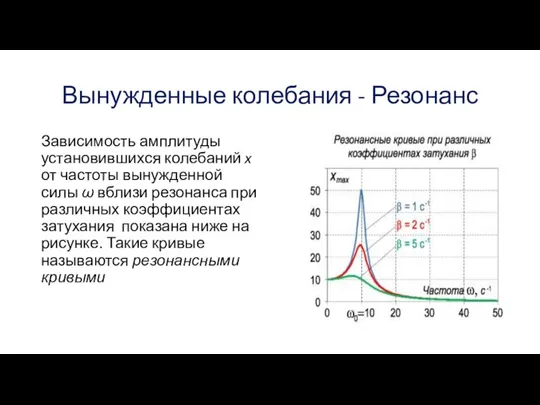
ω вблизи резонанса при различных коэффициентах затухания показана ниже на рисунке. Такие кривые называются резонансными кривыми
Слайд 48Вынужденные колебания - Резонанс

Слайд 50Колебания
Основные результаты этой лекции будут нам необходимы при изучении электрических колебаний и

волновых явлений
Слайд 51Задача 1
Груз массой m упал вертикально со скоростью V на чашку пружинных

весов. Масса чашки равна M, жесткость пружины – k. При ударе груз прилипает к чашке. Найти зависимость координаты чашки от времени после падения пластилина.
Слайд 53Задача 2
Вообразим, что между Москвой и Ленинградом прорыт тоннель, в котором проложены

рельсы.






















































 Эксперимент по физике высоких энергий
Эксперимент по физике высоких энергий Презентация на тему Генерирование переменного электрического тока
Презентация на тему Генерирование переменного электрического тока  Основы термодинамики. Лекция 2.3
Основы термодинамики. Лекция 2.3 Динамика точки в неинерциальной системе отсчета
Динамика точки в неинерциальной системе отсчета Муниципальное автономное общеобразовательное учреждение Муниципальное автономное общеобразовательное учреждение «Средняя об
Муниципальное автономное общеобразовательное учреждение Муниципальное автономное общеобразовательное учреждение «Средняя об Силы, действующие в магнитном поле: сила Ампера, сила Лоренца
Силы, действующие в магнитном поле: сила Ампера, сила Лоренца Сила трения
Сила трения Влажность. Решение задач. 8 класс
Влажность. Решение задач. 8 класс Токи в различных средах
Токи в различных средах Виды спектров
Виды спектров Электрические явления
Электрические явления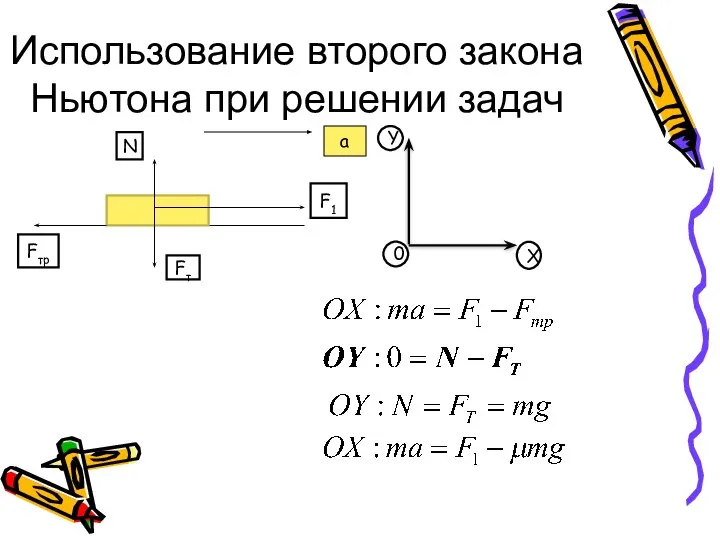 Использование второго закона Ньютона при решении задач
Использование второго закона Ньютона при решении задач Устройство термометра
Устройство термометра Преобразование энергии в тепловых процессах
Преобразование энергии в тепловых процессах Состав ядра атома. Энергия связи атомных ядер. Дефект масс
Состав ядра атома. Энергия связи атомных ядер. Дефект масс Путешествие в страну физики. Урок-викторина, 7 класс
Путешествие в страну физики. Урок-викторина, 7 класс Реализация проекта строительства атомной электростанции в Республике Беларусь
Реализация проекта строительства атомной электростанции в Республике Беларусь Колебательный контур. Получение электромагнитных колебаний
Колебательный контур. Получение электромагнитных колебаний Альтернативные источники энергии
Альтернативные источники энергии Демонстрационный вариант контрольных измерительных материалов для проведения в 2016 году государственного экзамена по физике
Демонстрационный вариант контрольных измерительных материалов для проведения в 2016 году государственного экзамена по физике Презентация-ФТП (Тема3-деф и разруш)-17
Презентация-ФТП (Тема3-деф и разруш)-17 Миграция Кирхгофа
Миграция Кирхгофа Основы медицинской и биологической физики. Лекция 4. Часть 2
Основы медицинской и биологической физики. Лекция 4. Часть 2 Возможности расчетов на сейсмические воздействия в программном комплексе ЛИРА 10.8
Возможности расчетов на сейсмические воздействия в программном комплексе ЛИРА 10.8 Ядерные реакции. Энергия связи атомного ядра
Ядерные реакции. Энергия связи атомного ядра Механическая лаборатория
Механическая лаборатория Физика в загадках
Физика в загадках Давление. Обозначение и единицы измерения давления
Давление. Обозначение и единицы измерения давления