Содержание
- 2. МЕХАНИКА (греч. μηχανική – искусство построения машин) – основной раздел физики; наука о механическом движении материальных
- 3. Разделы теоретической механики: 1. Статика 2. Кинематика 3. Динамика
- 4. СТАТИКА (от греч. States – стоящий) раздел механики, в котором излагается общее учение о силах и
- 5. В статике твердого тела рассматриваются две основные проблемы: Сложение сил и приведение систем сил, действующих на
- 6. СИЛА – количественная мера механического взаимодействия материальных тел. Сила является величиной векторной. Ее действие на тело
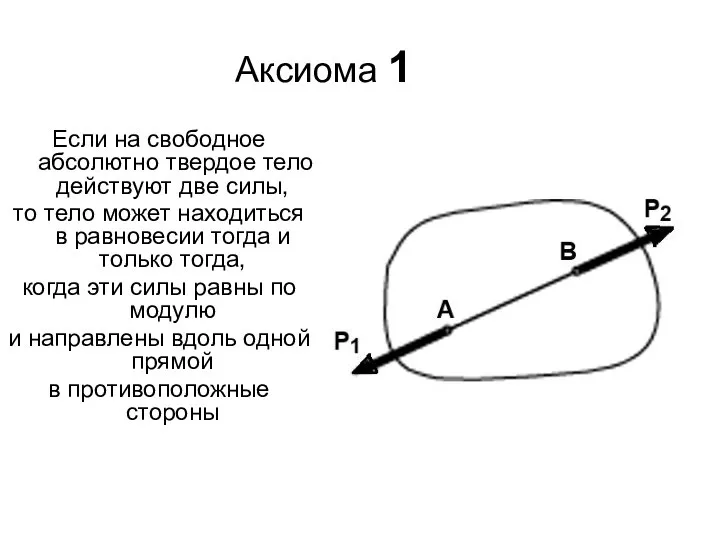
- 7. Аксиома 1 Если на свободное абсолютно твердое тело действуют две силы, то тело может находиться в
- 8. Аксиома 2 Действие данной системы сил на абсолютно твердое тело не изменится, если к ней прибавить
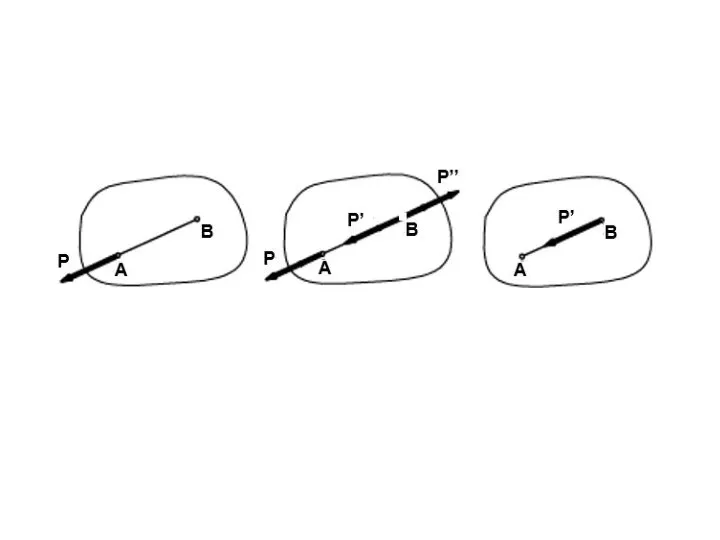
- 9. Следствие из 1-й и 2-й аксиом Действие силы на абсолютно твердое тело не изменится, если перенести
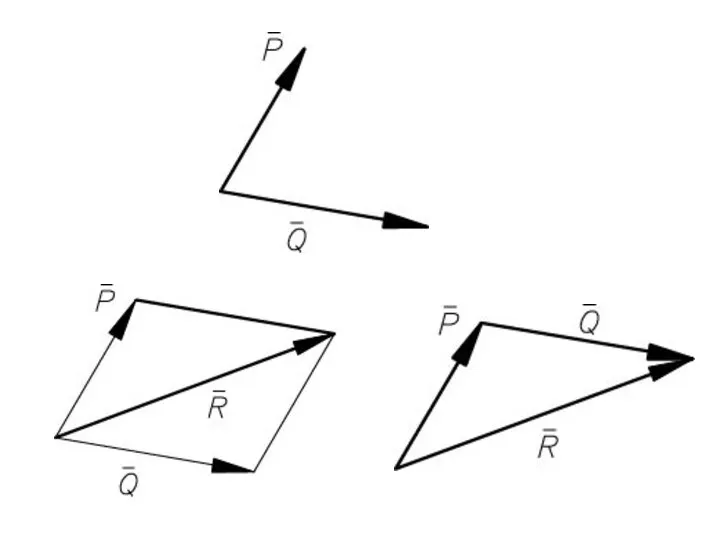
- 11. Аксиома 3 (аксиома параллелограмма сил). Две силы, приложенные к телу в одной точке, имеют равнодействующую, приложенную
- 13. Аксиома 4 При всяком действии одного материального тела на другое имеет место такое же по величине,
- 14. Аксиома 5 (принцип отвердевания) Равновесие изменяемого (деформируемого) тела, находящегося под действием данной системы сил, не нарушится,
- 15. КИНЕМАТИЧЕСКОЕ СОСТОЯНИЕ - состояние материальной точки или системы материальных точек, полностью и однозначно определяемое временем, пространственными
- 16. ЭКВИВАЛЕНТНЫЕ СИСТЕМЫ СИЛ Если одну систему сил , действующую на свободное твердое тело, можно заменить другой
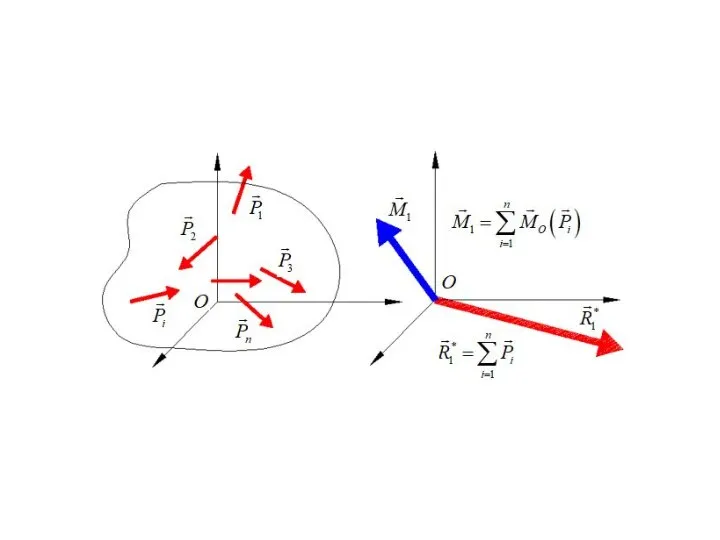
- 17. РАВНОДЕЙСТВУЮЩАЯ СИСТЕМЫ СИЛ – сила , эквивалентная данной системе сил :
- 18. СХОДЯЩИЕСЯ СИЛЫ - система сил, линии действия которых пересекаются в одной точке
- 19. РАВНОДЕЙСТВУЮЩАЯ СИСТЕМЫ СХОДЯЩИХСЯ СИЛ равна их геометрической сумме, а линия действия проходит через точку пересечения сил
- 21. Теорема трех сил: «Если три силы, лежащие в одной плоскости, уравновешены, то линии их действия пересекаются
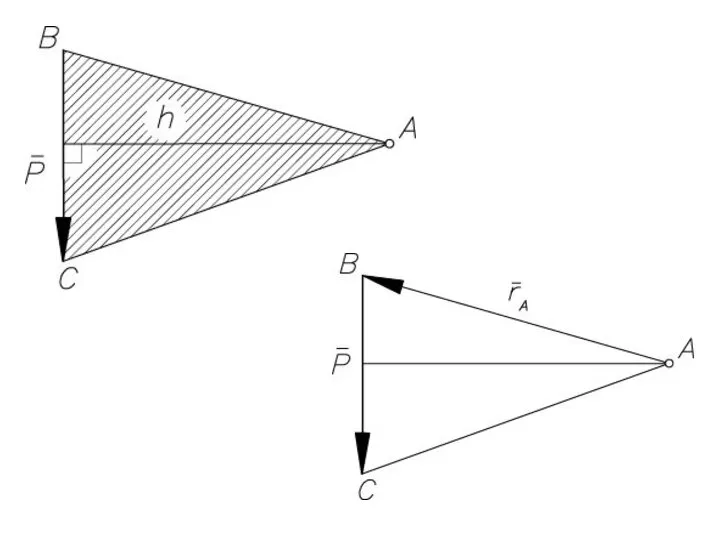
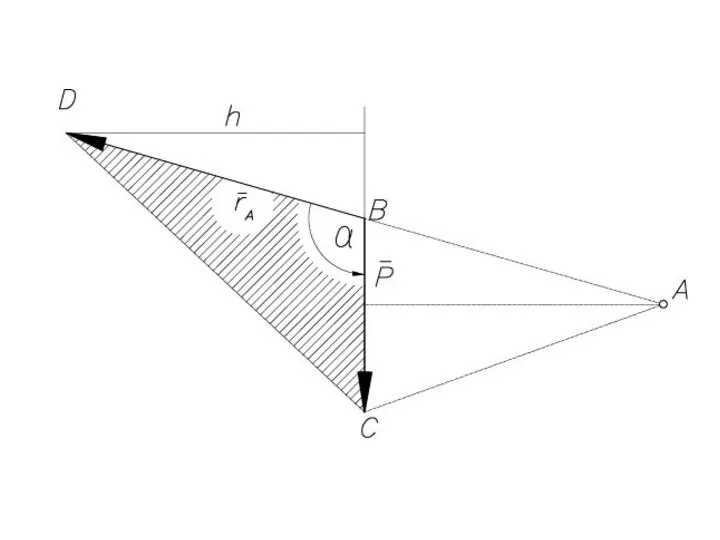
- 22. МОМЕНТ СИЛЫ относительно центра О называется вектор , равный векторному произведению радиуса вектора , соединяющего центр
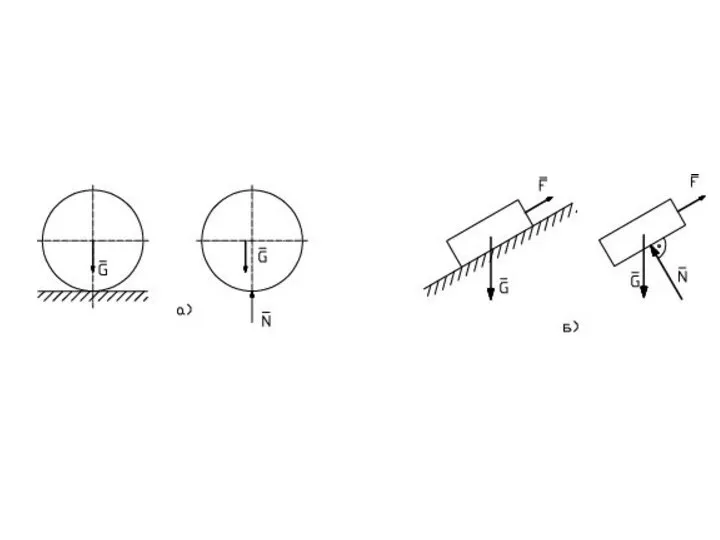
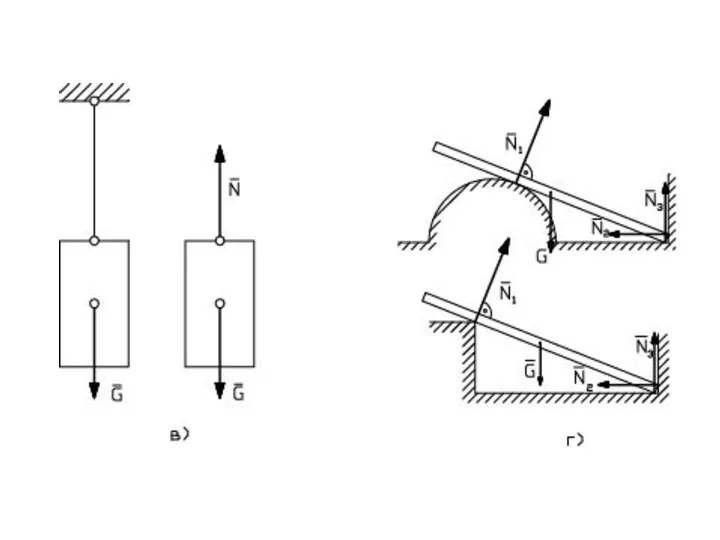
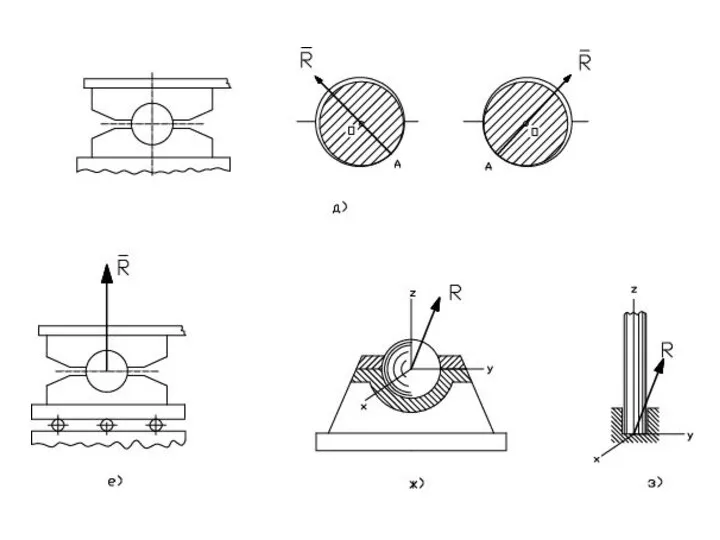
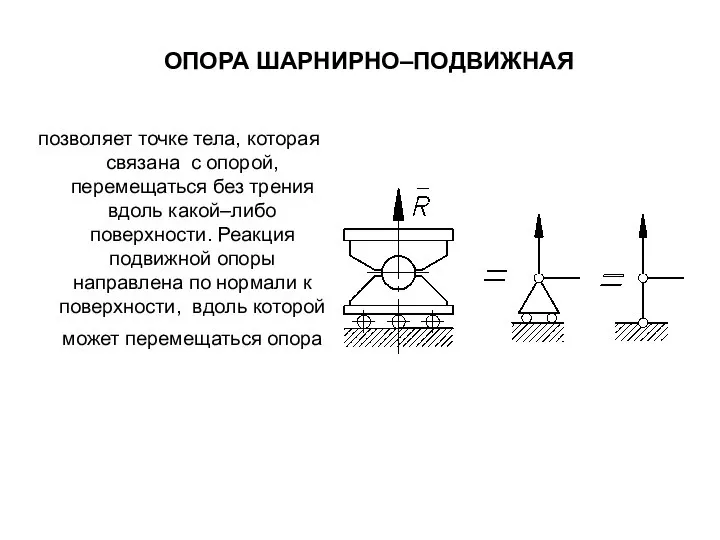
- 29. ОПОРА ШАРНИРНО–ПОДВИЖНАЯ позволяет точке тела, которая связана с опорой, перемещаться без трения вдоль какой–либо поверхности. Реакция
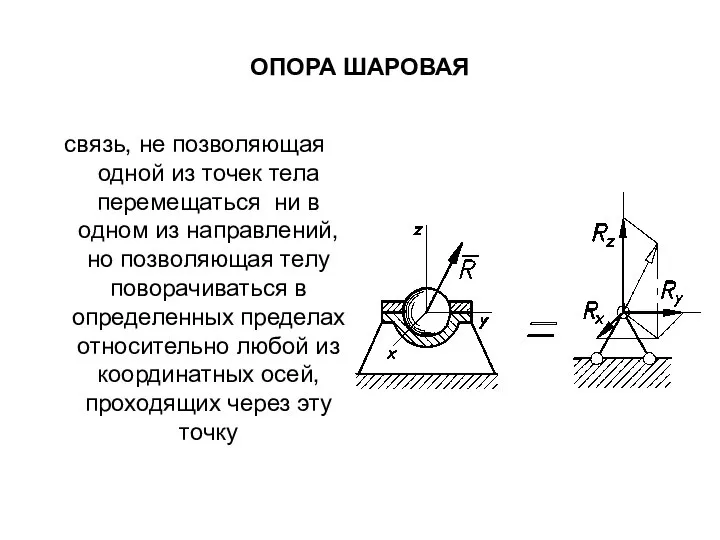
- 30. ОПОРА ШАРОВАЯ связь, не позволяющая одной из точек тела перемещаться ни в одном из направлений, но
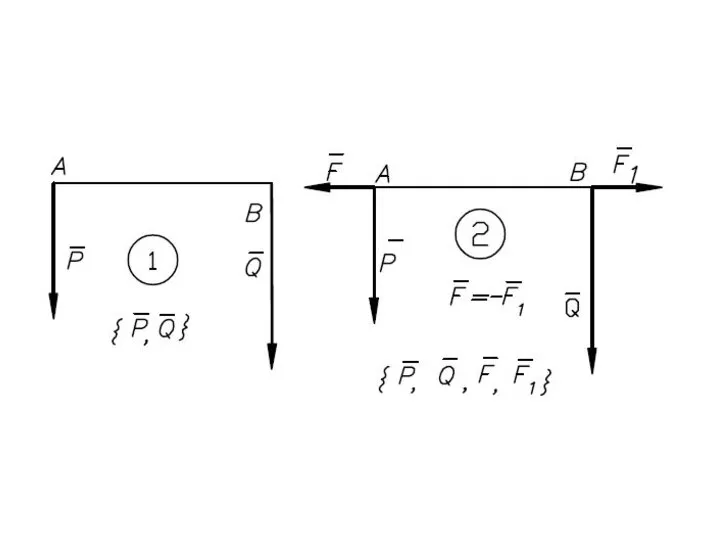
- 31. Равнодействующая параллельных сил, направленных в одну сторону
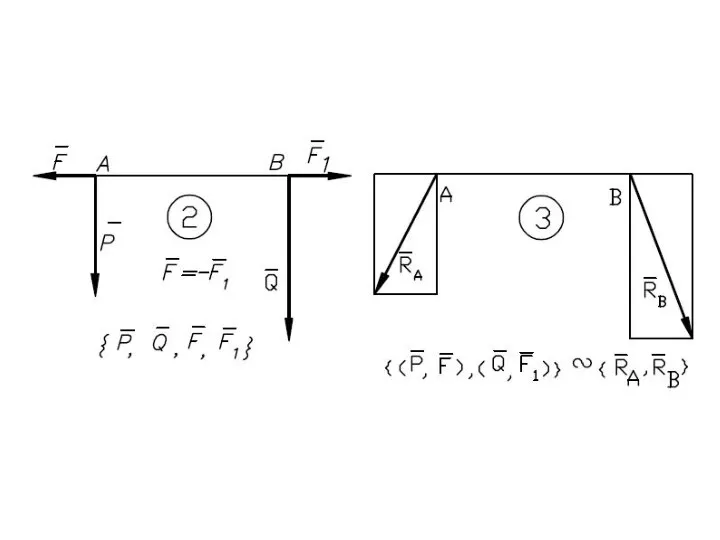
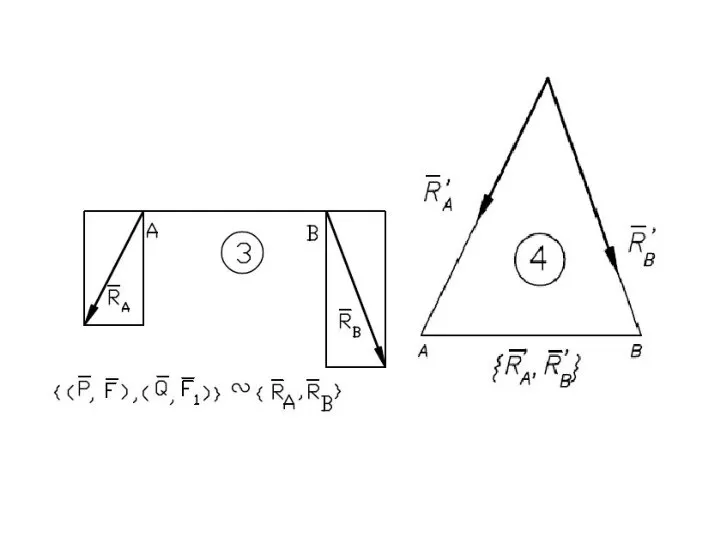
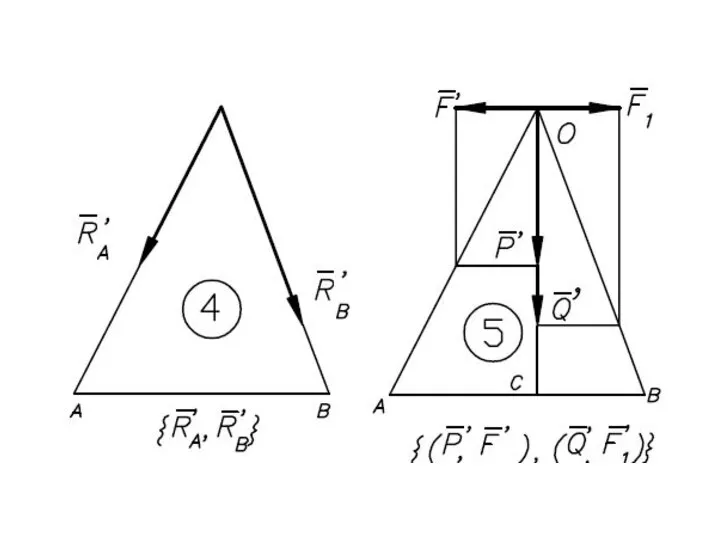
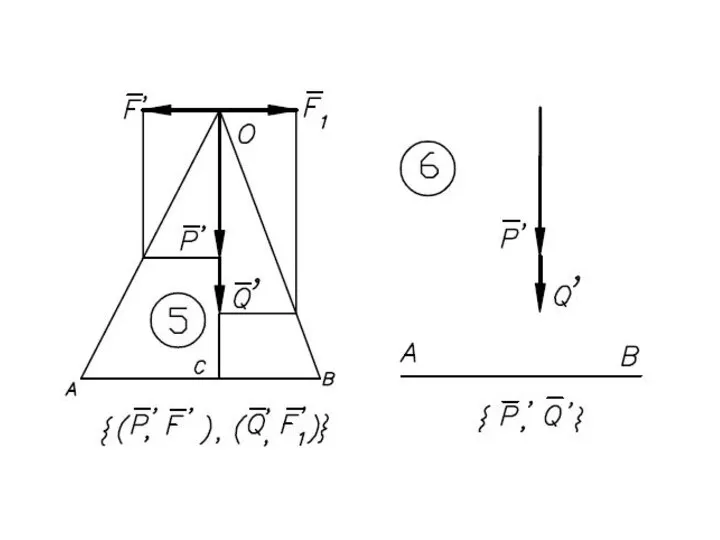
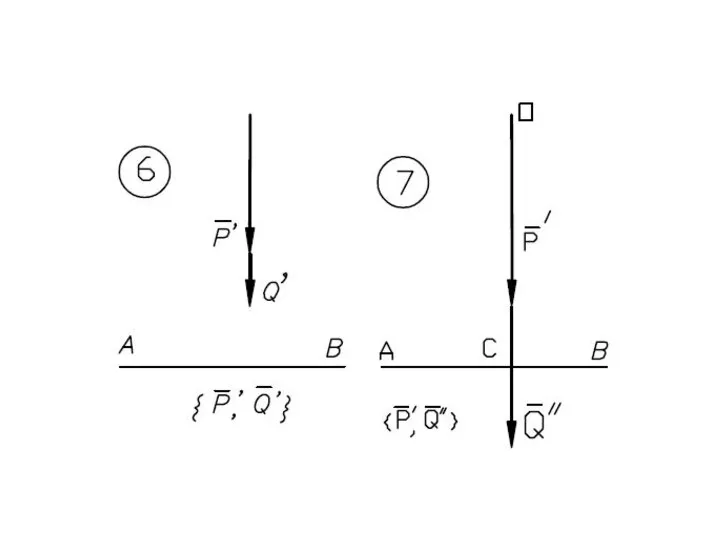
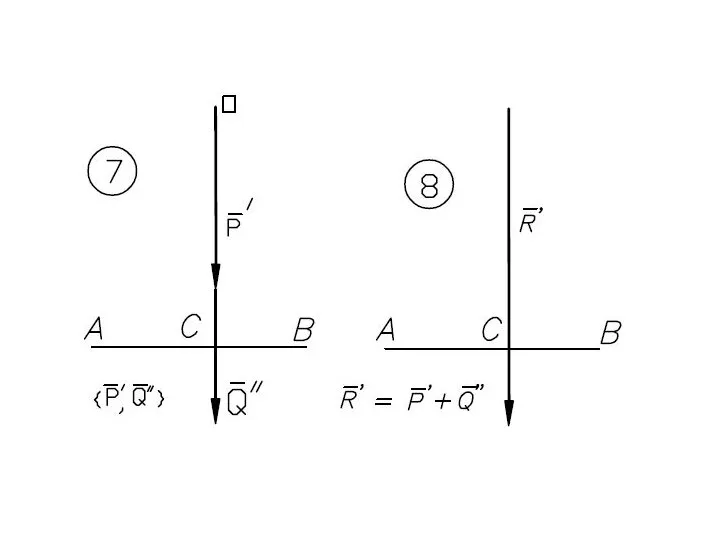
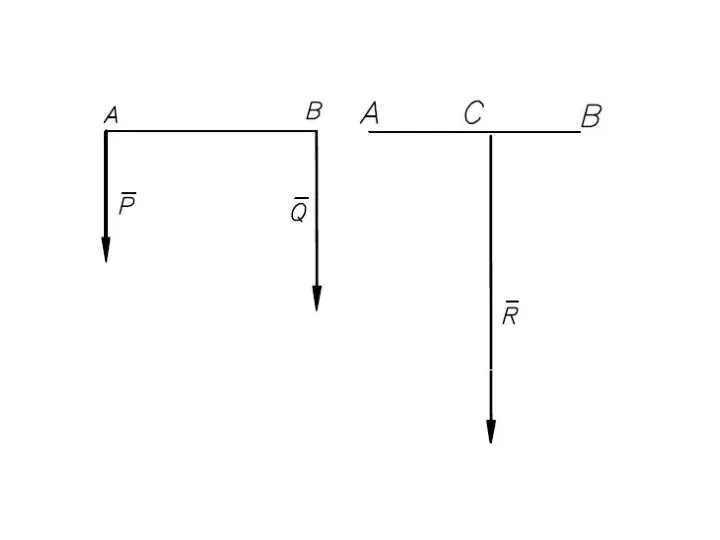
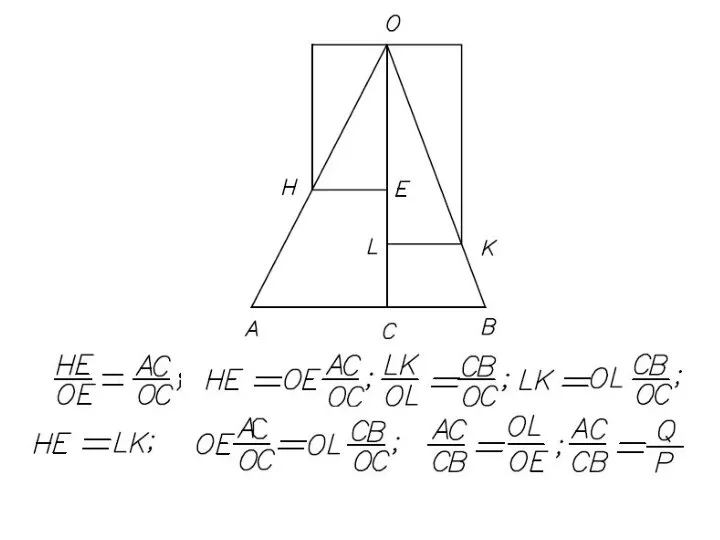
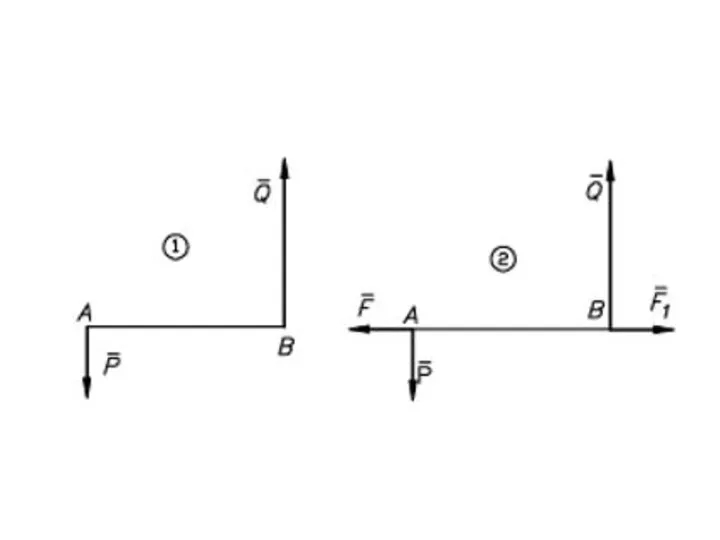
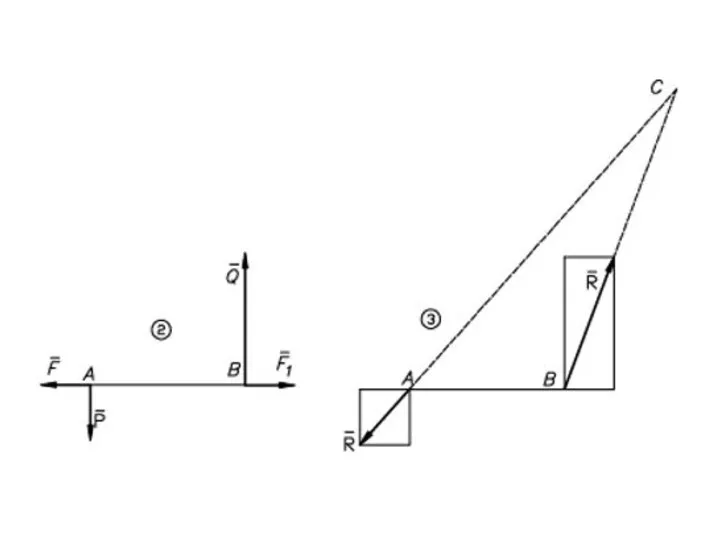
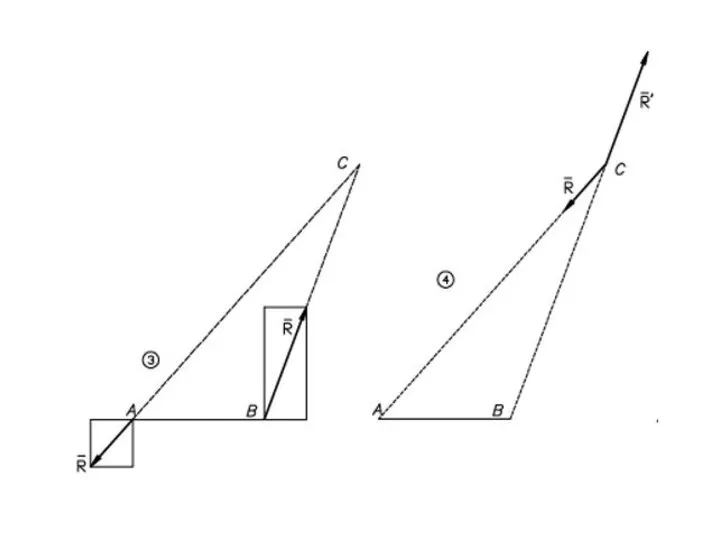
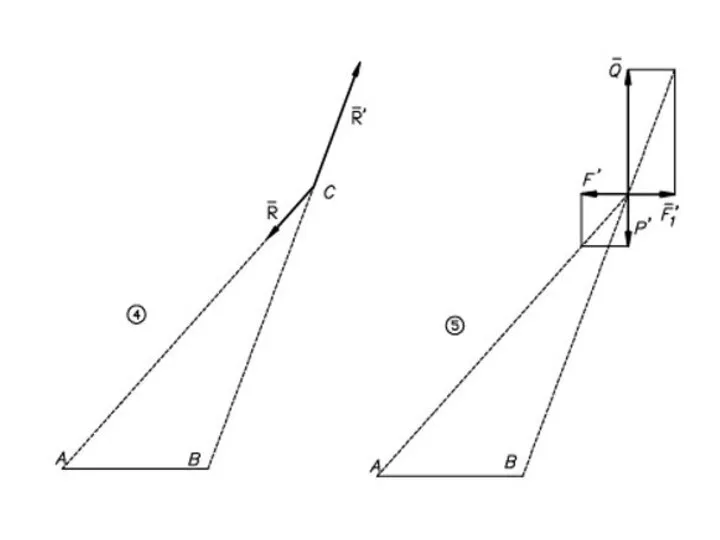
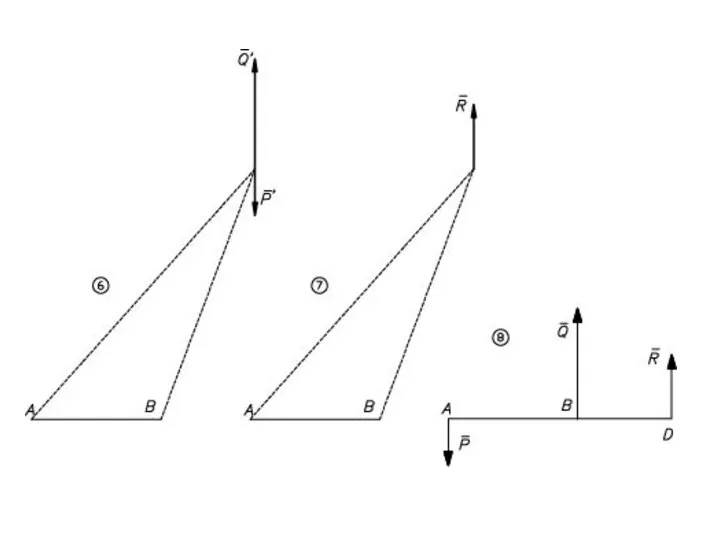
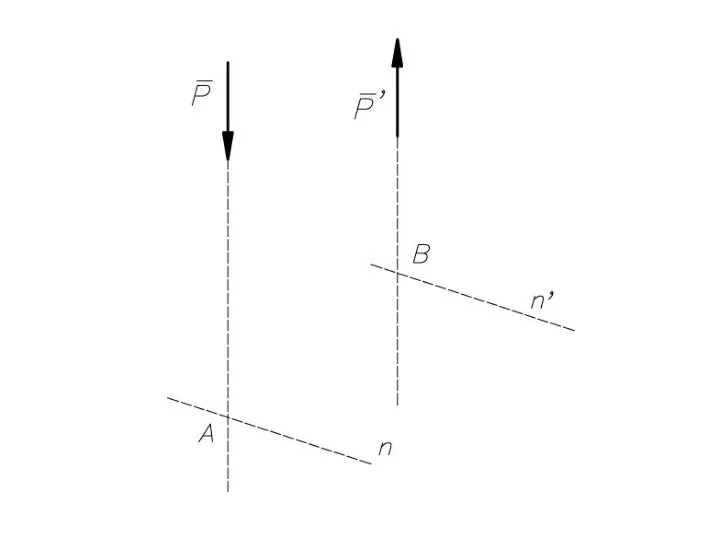
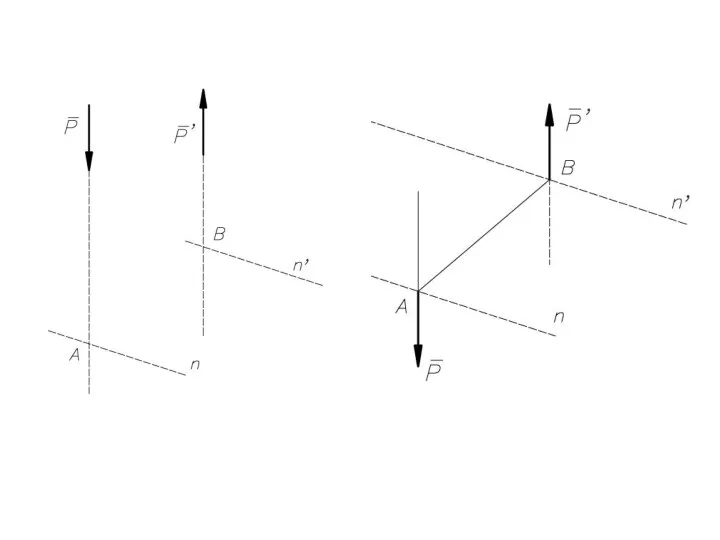
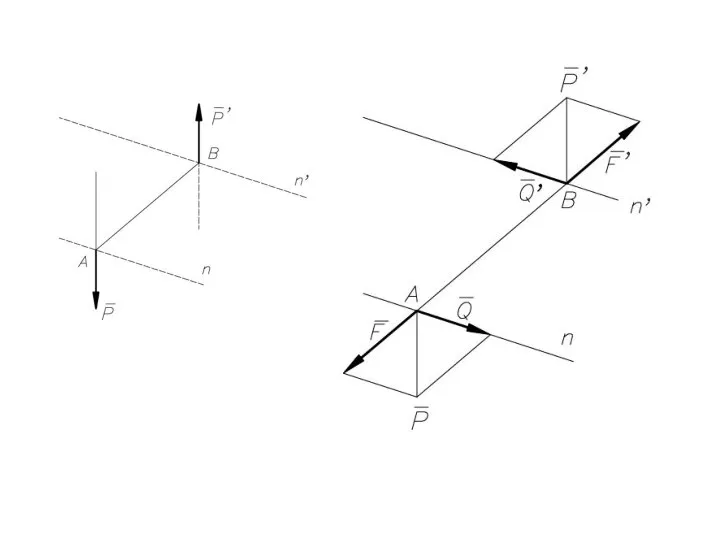
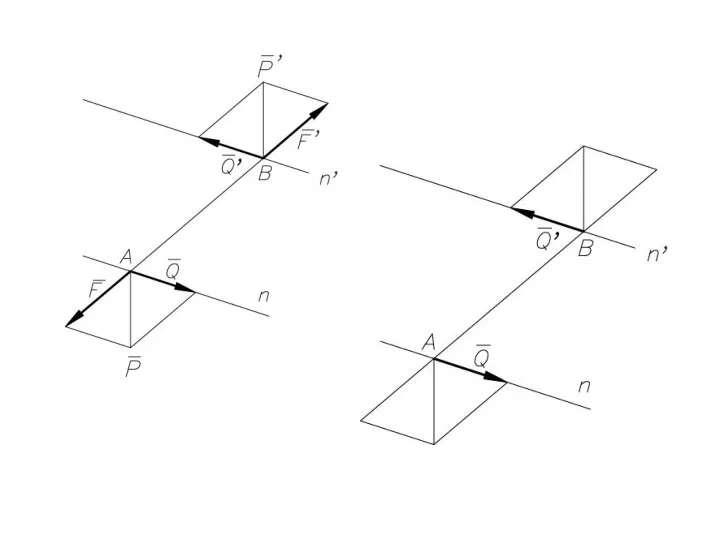
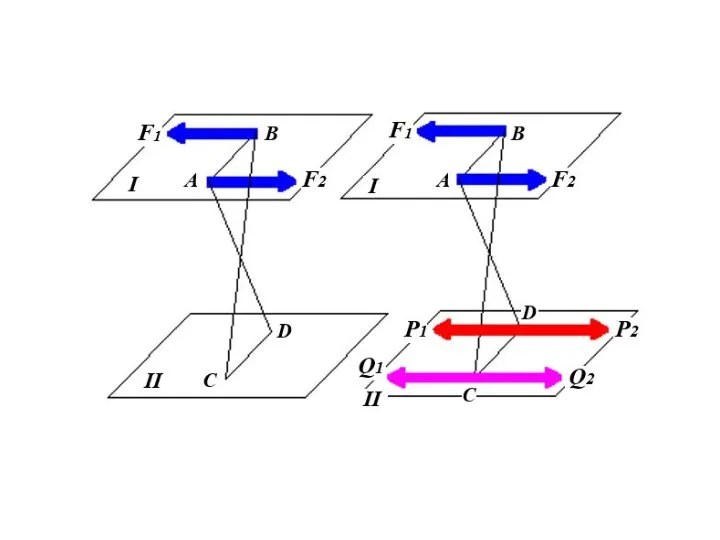
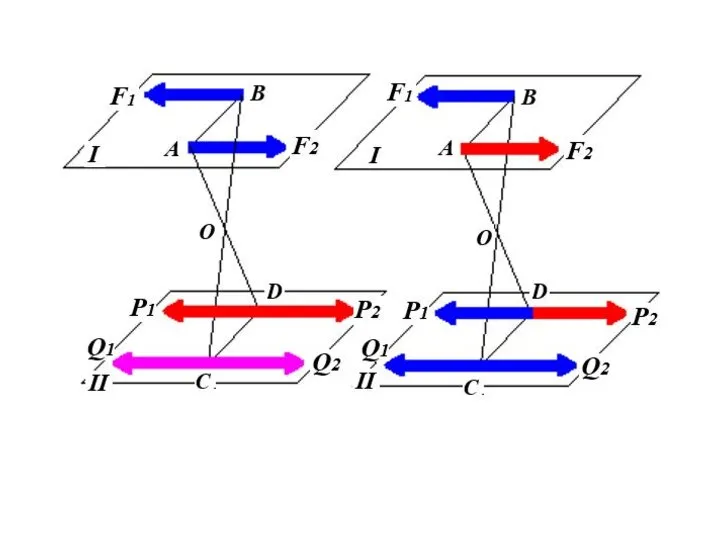
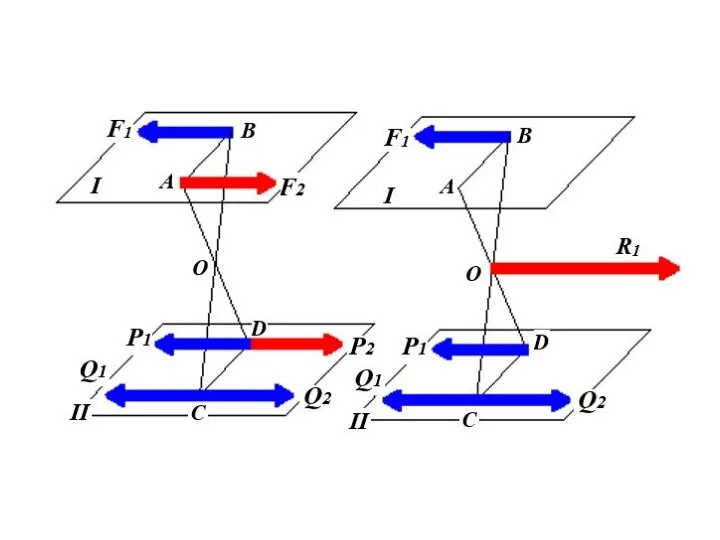
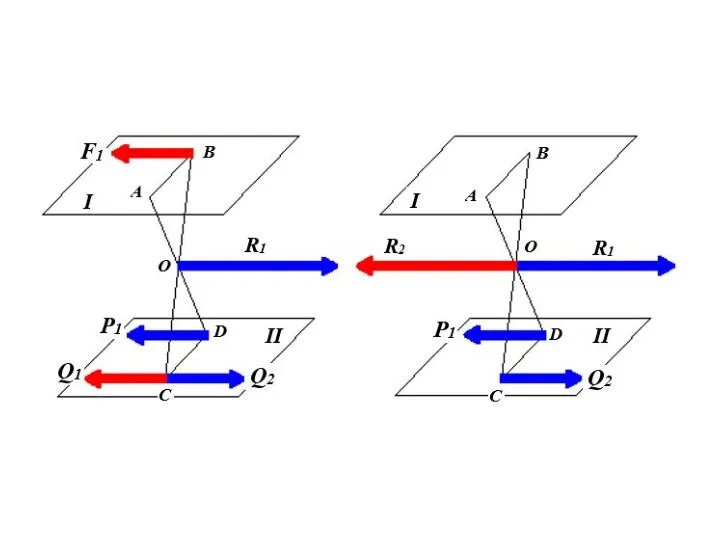
- 41. Равнодействующая параллельных сил, направленных в разные стороны, не равных по модулю
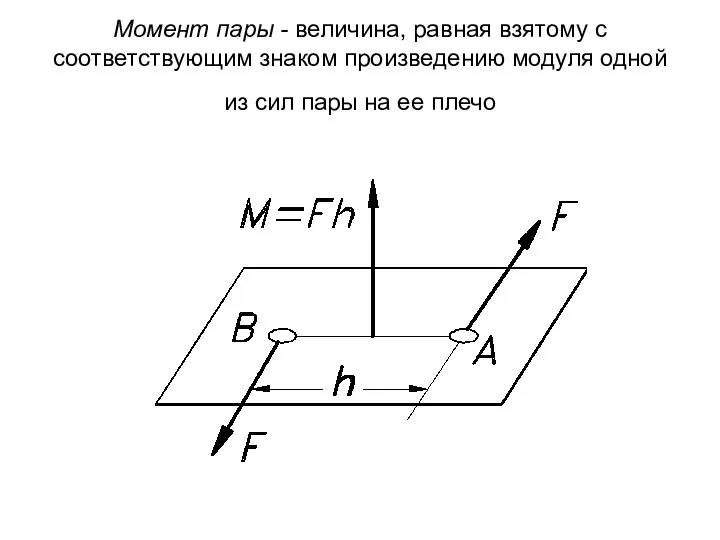
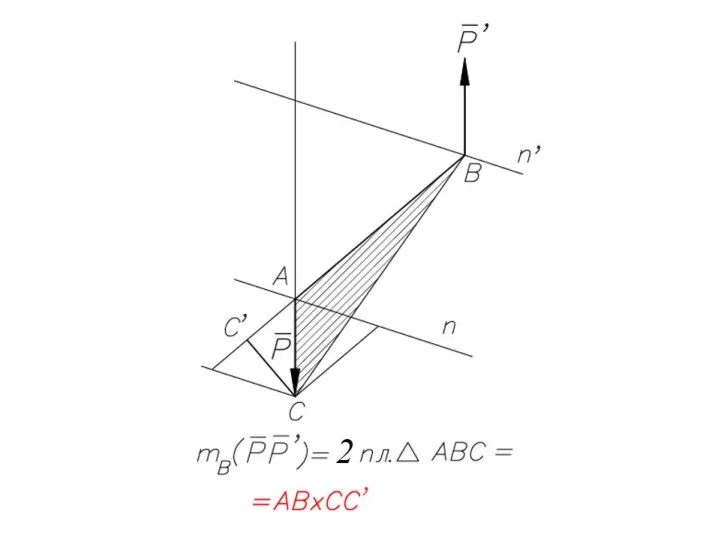
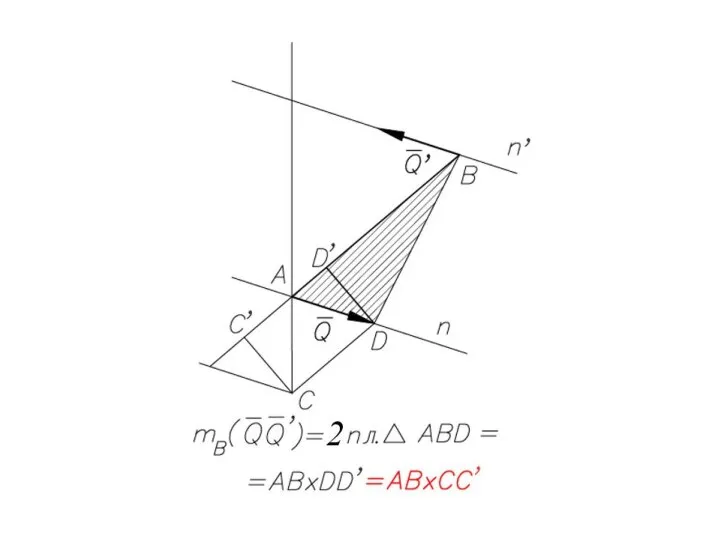
- 48. Момент пары - величина, равная взятому с соответствующим знаком произведению модуля одной из сил пары на
- 49. МОМЕНТ СИЛ ПАРЫ ОТНОСИТЕЛЬНО ПРОИЗВОЛЬНОГО ЦЕНТРА : геометрическая сумма моментов сил пары относительно любого центра, как
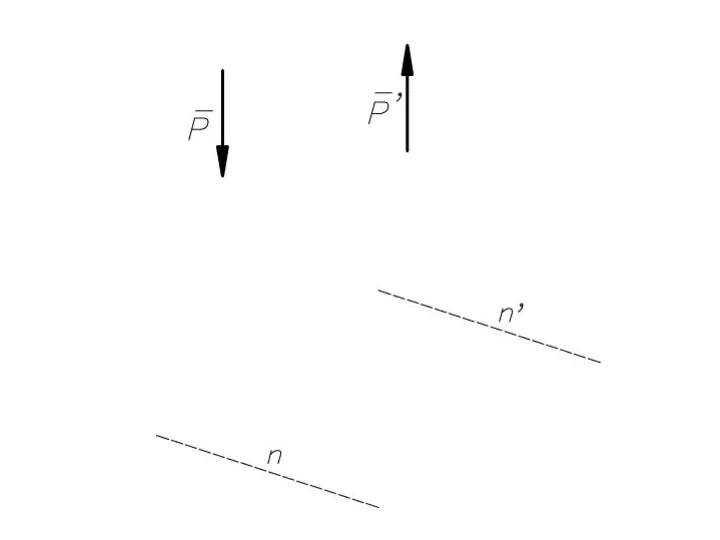
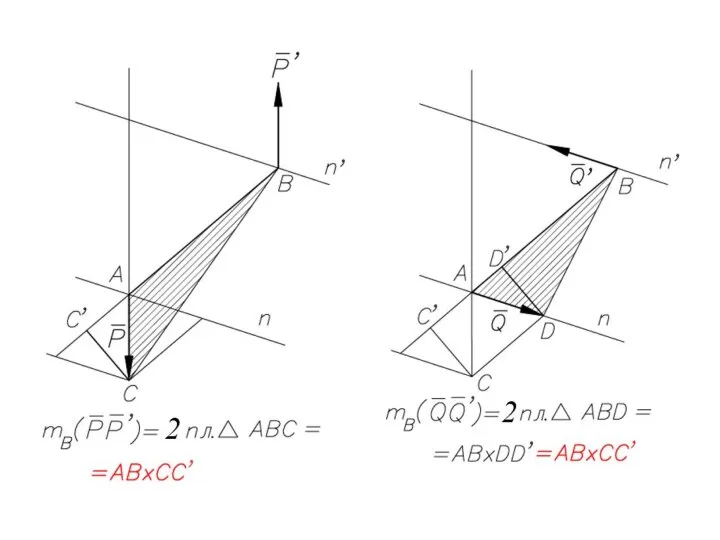
- 50. Эквивалентность пар на плоскости Не изменяя оказываемого на тело действия, можно пару сил, приложенную к абсолютно
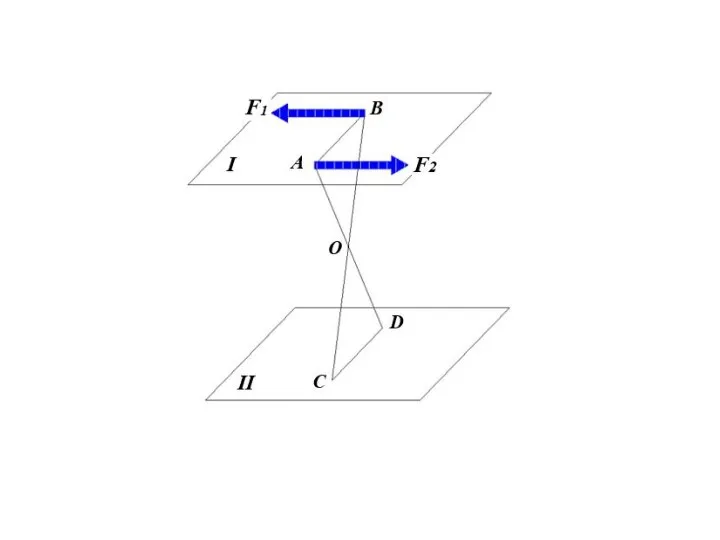
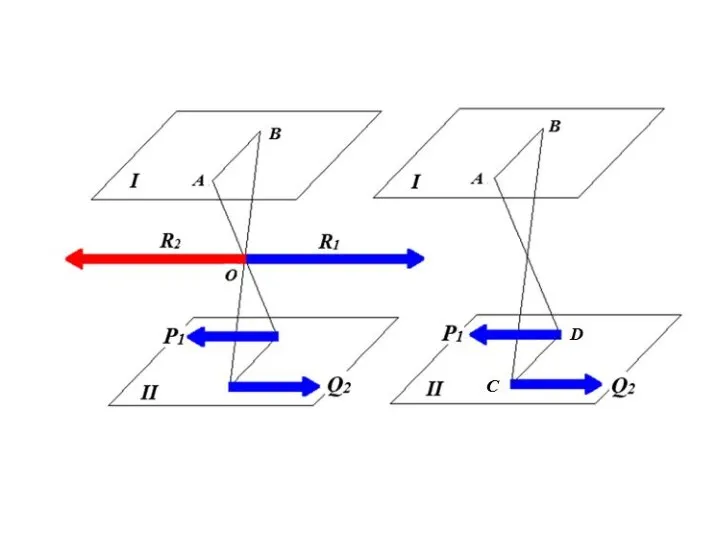
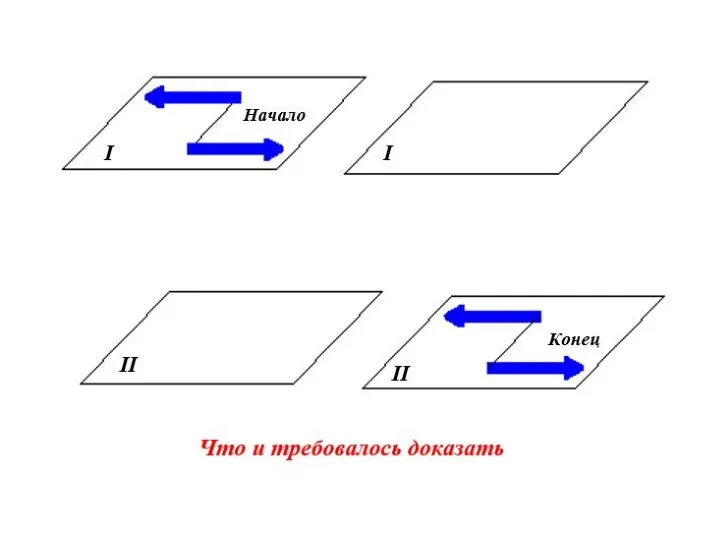
- 59. Эквивалентность пар в пространстве Не изменяя оказываемого на тело действия, можно пару сил, приложенную к абсолютно
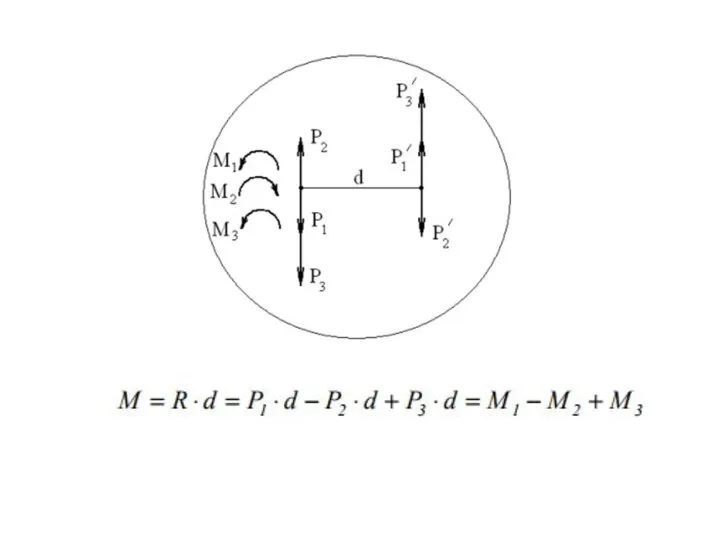
- 67. Теорема о сложении пар на плоскости: система пар, лежащих в одной плоскости, эквивалентна одной паре, лежащей
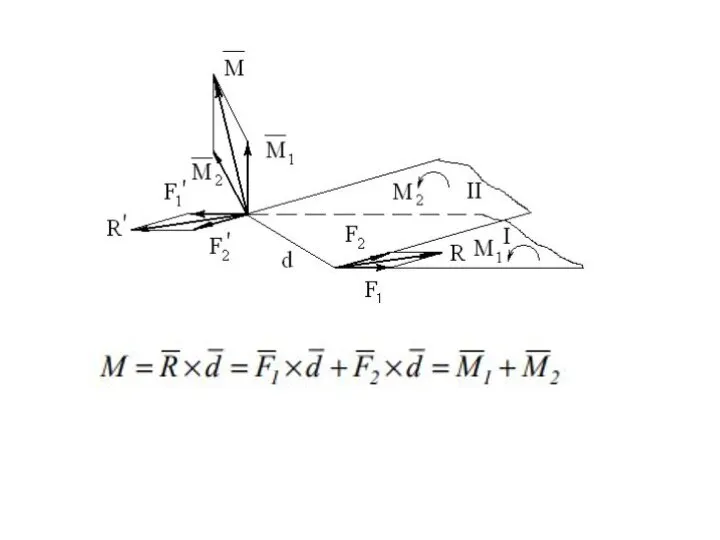
- 69. Теорема о сложении пар в пространстве: любая система пар, действующих на абсолютно твердое тело, эквивалентна одной
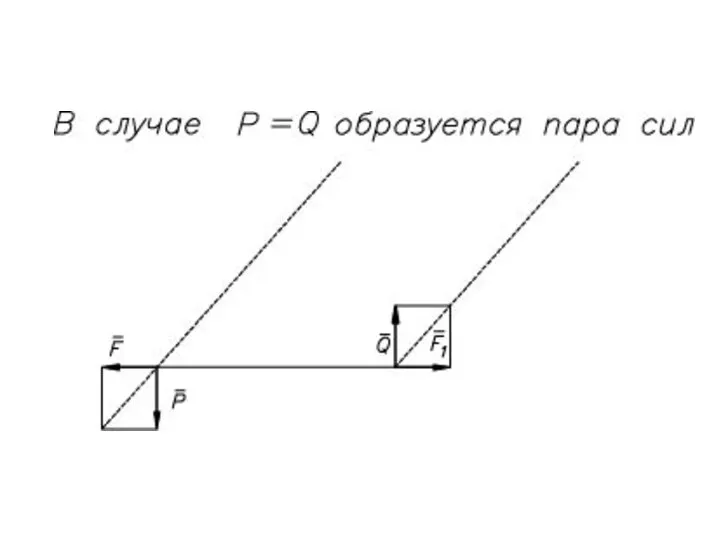
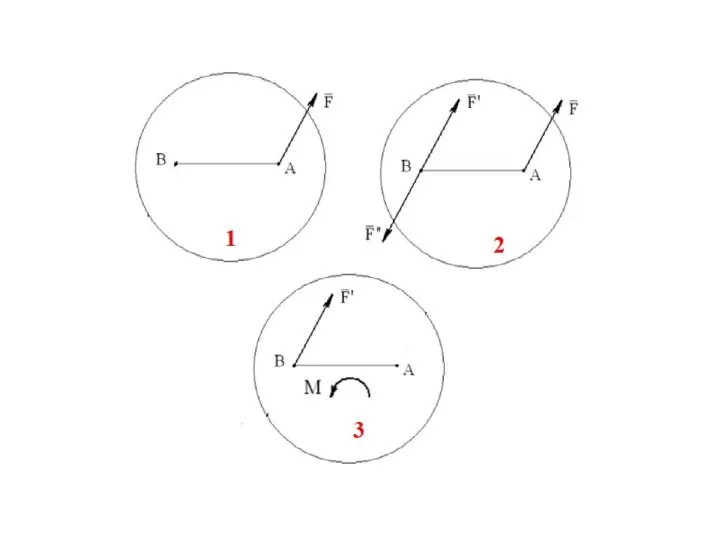
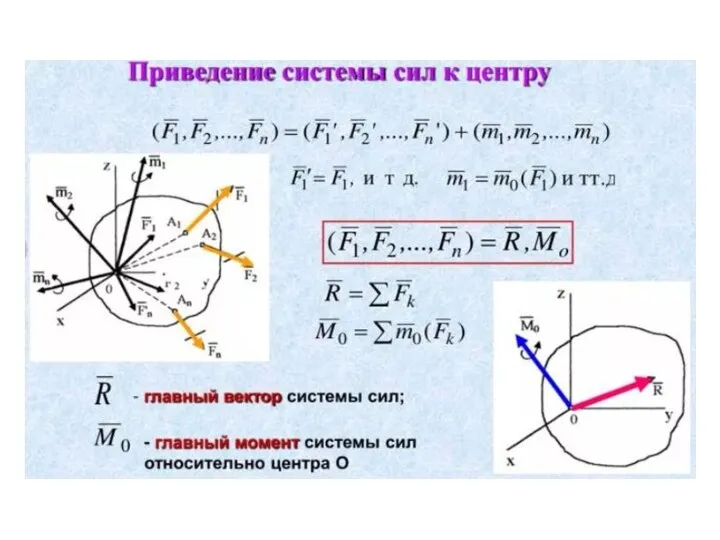
- 71. Теорема о параллельном переносе силы (теорема Пуансо): силу, приложенную к абсолютно твердому телу, можно, не изменяя
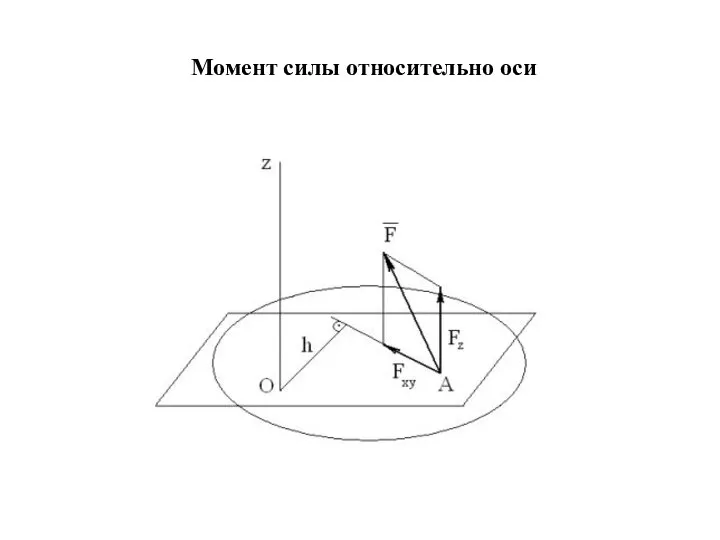
- 73. Момент силы относительно оси
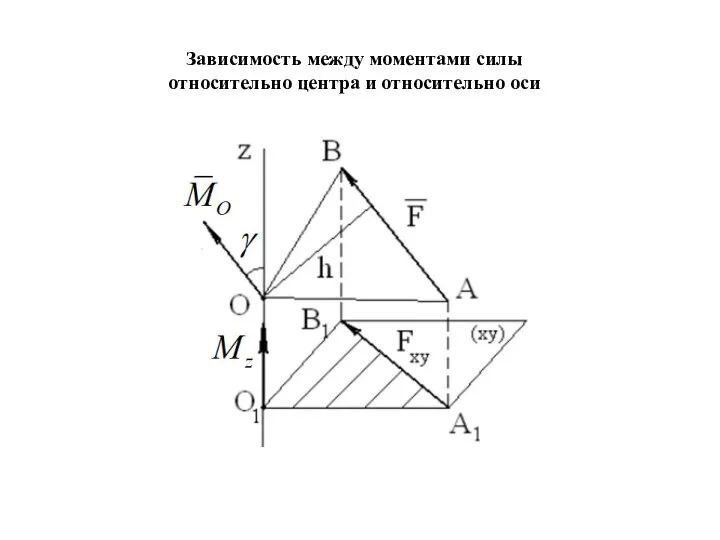
- 74. Зависимость между моментами силы относительно центра и относительно оси
- 78. ИНВАРИАНТЫ СИСТЕМЫ СИЛ
- 79. Инварианты – величины, неизменные при некотором преобразовании Статические инварианты – величины, не зависящие от выбора центра
- 83. Скачать презентацию


















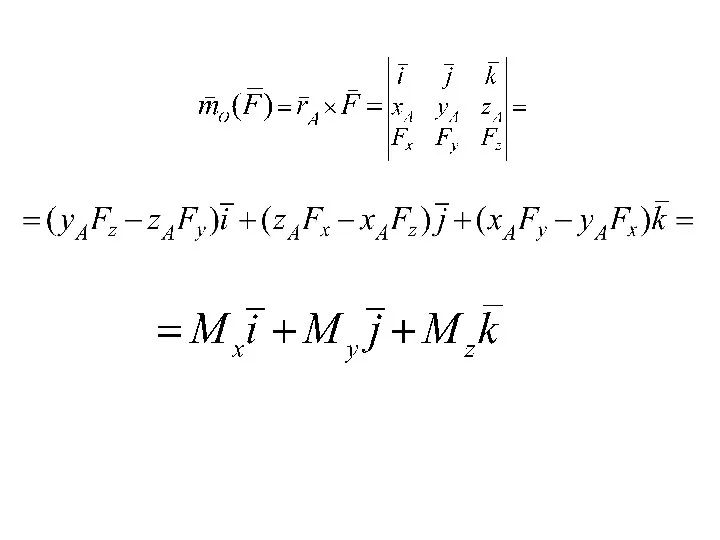












 Flyer engine BYD 368
Flyer engine BYD 368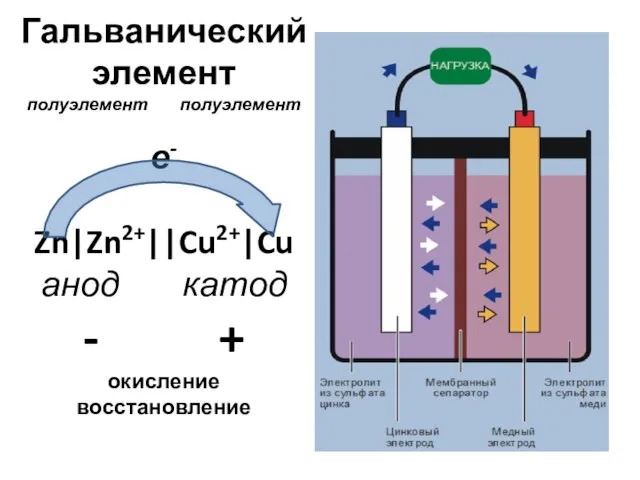 Гальванический элемент, полуэлемент, полуэлемент, е- Zn|Zn2+||Cu2+|Cu, анод, катод, - +, окисление, восстановление
Гальванический элемент, полуэлемент, полуэлемент, е- Zn|Zn2+||Cu2+|Cu, анод, катод, - +, окисление, восстановление Kursovoy_proekt_tsilindricheskogo_reduktora_otredaktirovan
Kursovoy_proekt_tsilindricheskogo_reduktora_otredaktirovan Молярная масса
Молярная масса Источники света. Распространение света
Источники света. Распространение света Презентация на тему Радиационное и электромагнитное излучение
Презентация на тему Радиационное и электромагнитное излучение  Наноматериалы. Оптические свойства
Наноматериалы. Оптические свойства Фононы. Акустические и оптические фононы
Фононы. Акустические и оптические фононы Передняя и задняя подвески ГАЗ-3309
Передняя и задняя подвески ГАЗ-3309 Тест. 8 класс
Тест. 8 класс Формула бинома Ньютона
Формула бинома Ньютона Professional english for mechanics
Professional english for mechanics Презентация на тему Самоиндукция
Презентация на тему Самоиндукция  Ускорение
Ускорение ЭДС индукции
ЭДС индукции Статика
Статика Исследование возникновения и развития скольжения в поликристаллических образцах алюминия с помощью лазерной методики
Исследование возникновения и развития скольжения в поликристаллических образцах алюминия с помощью лазерной методики Коэффициент полезного действия механизма. Дома: §61 Повторить «золотое правило» механики. Познакомиться с понятием коэффициента полезного действия как основной характеристики рабочего механизма.
Коэффициент полезного действия механизма. Дома: §61 Повторить «золотое правило» механики. Познакомиться с понятием коэффициента полезного действия как основной характеристики рабочего механизма.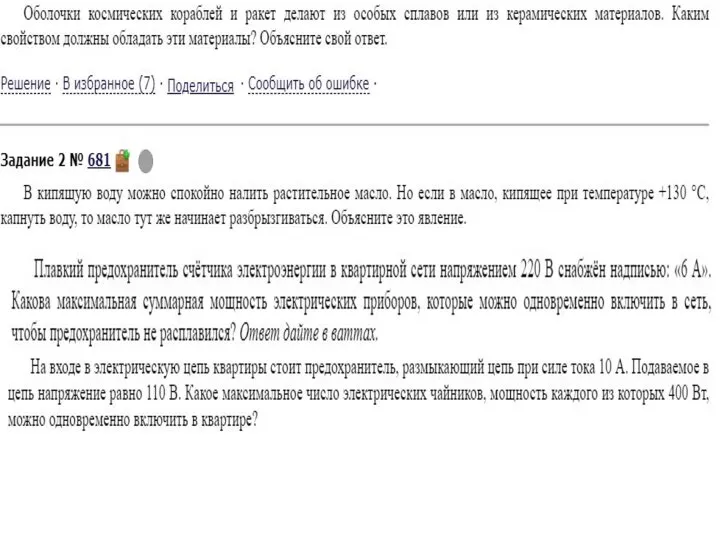 Задания по физике
Задания по физике Геометрическая оптика
Геометрическая оптика Действие магнитного поля на проводник с током. Сила Ампера
Действие магнитного поля на проводник с током. Сила Ампера Магнитное поле и его характеристики
Магнитное поле и его характеристики Колебательное движение. Свободные колебания
Колебательное движение. Свободные колебания Сопротивление потоку
Сопротивление потоку Переменный электрический ток
Переменный электрический ток Сопротивление материалов
Сопротивление материалов Презентация на тему Строение и свойства вещества
Презентация на тему Строение и свойства вещества  Расчет конфигурации аккумуляторных батарей для ИБП GE Digital Energy™
Расчет конфигурации аккумуляторных батарей для ИБП GE Digital Energy™