Содержание
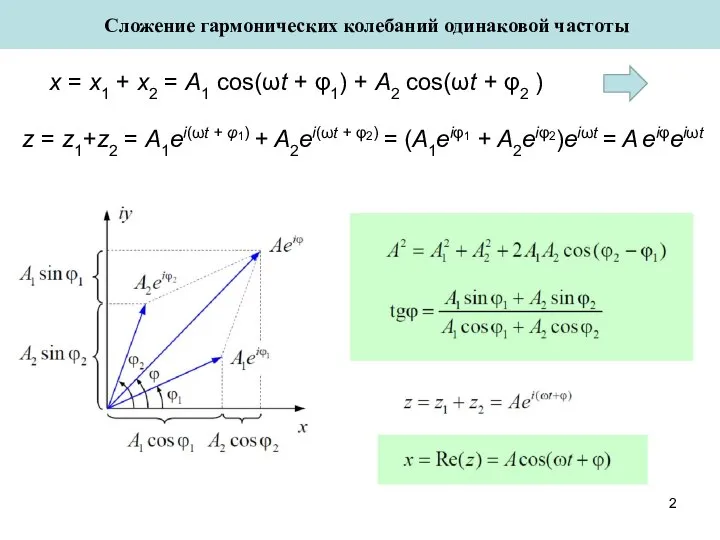
- 2. x = x1 + x2 = A1 cos(ωt + φ1) + A2 cos(ωt + φ2 )
- 3. Интерференция света Принцип суперпозиции: При наложении световых волн результирующий световой вектор является суммой световых векторов отдельных
- 4. Результат сложения зависит от разности фаз δ: Интерференция: При наложении гармонических (в общем случае когерентных) световых
- 5. Разность фаз колебаний
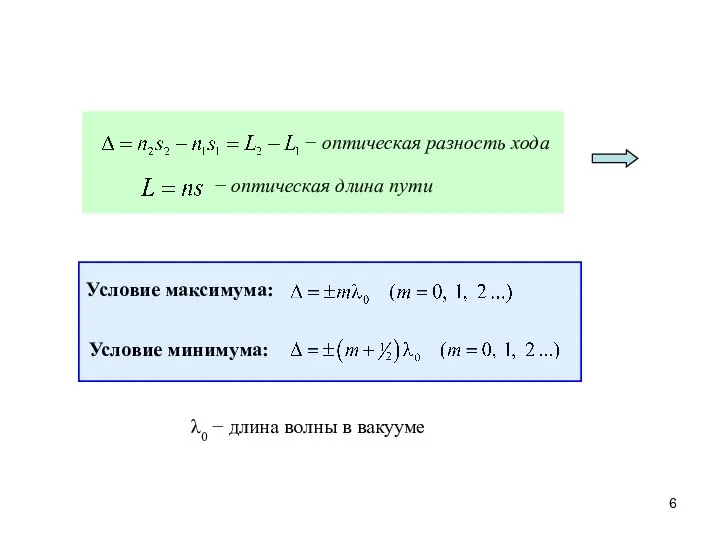
- 6. − оптическая разность хода − оптическая длина пути Условие максимума: Условие минимума: λ0 − длина волны
- 7. Временная когерентность Когерентность − согласованное протекание колебательных (волновых) процессов. Временная когерентность − когерентность колебаний, совершаемых в
- 8. 1. − интерференция отсутствует 2. − интерференция присутствует − время когерентности − длина когерентности (расстояние, при
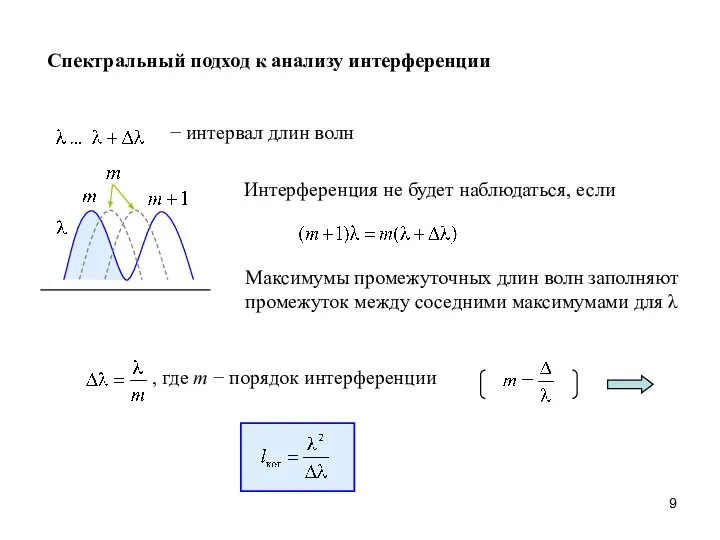
- 9. Спектральный подход к анализу интерференции − интервал длин волн Интерференция не будет наблюдаться, если Максимумы промежуточных
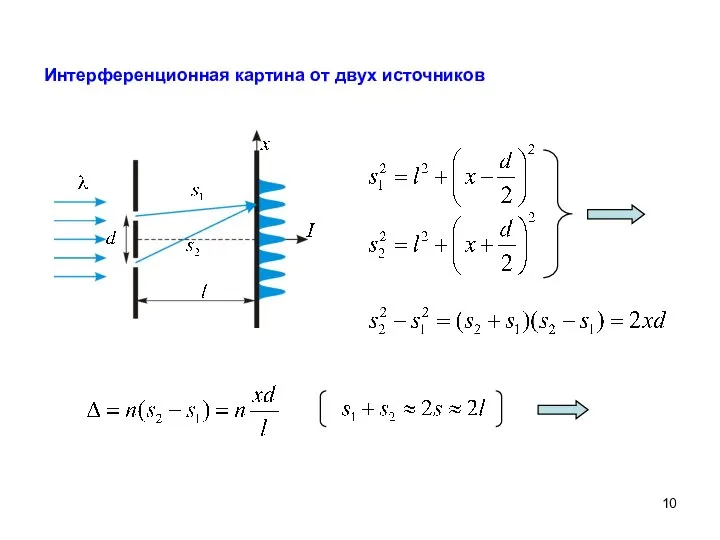
- 10. Интерференционная картина от двух источников
- 11. Максимумы: Минимумы: – длина волны в среде Ширина интерференционной полосы − расстояние между соседними минимумами Расстояние
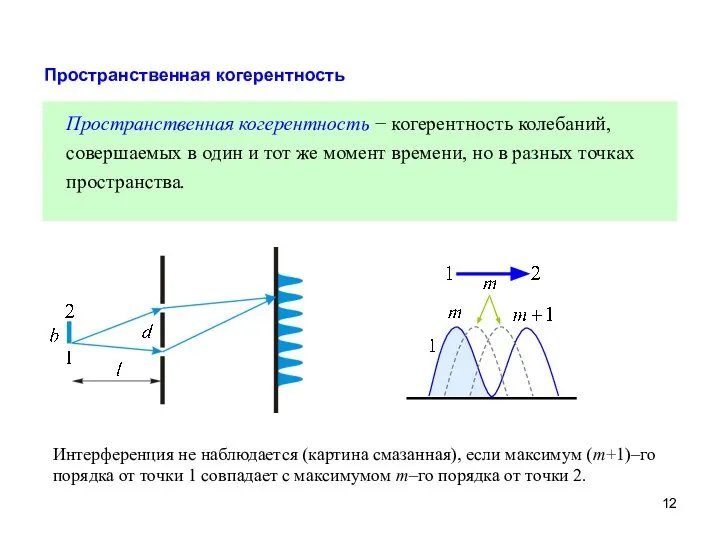
- 12. Пространственная когерентность Пространственная когерентность − когерентность колебаний, совершаемых в один и тот же момент времени, но
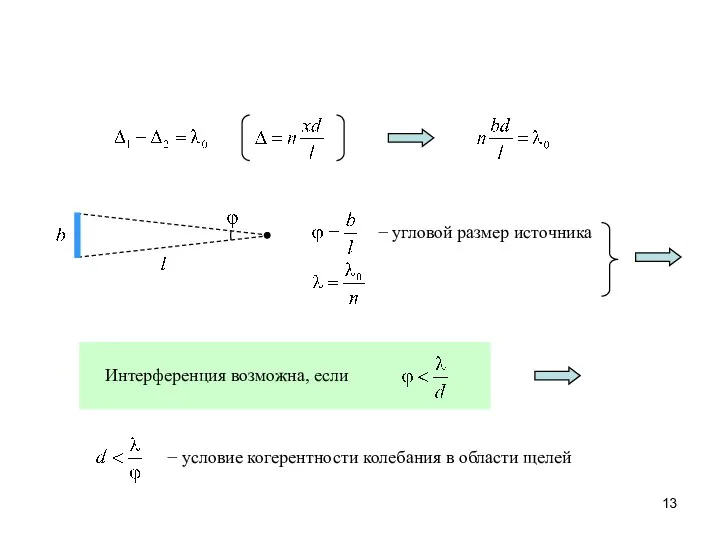
- 13. − угловой размер источника Интерференция возможна, если − условие когерентности колебания в области щелей
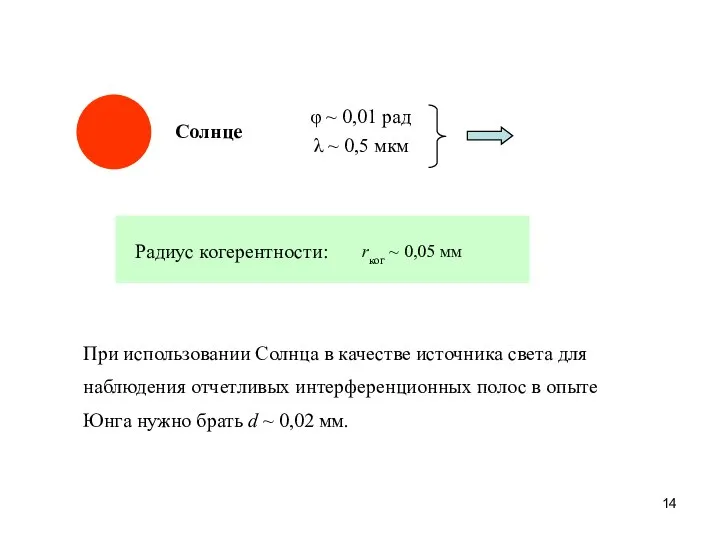
- 14. Солнце При использовании Солнца в качестве источника света для наблюдения отчетливых интерференционных полос в опыте Юнга
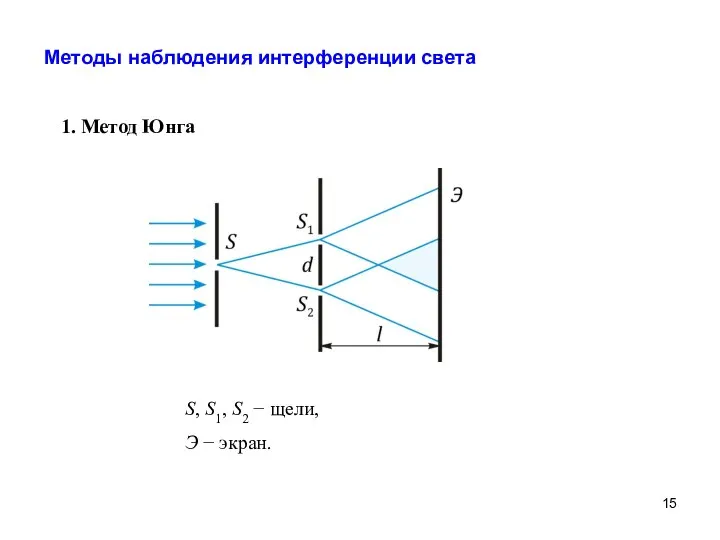
- 15. Методы наблюдения интерференции света 1. Метод Юнга S, S1, S2 − щели, Э − экран.
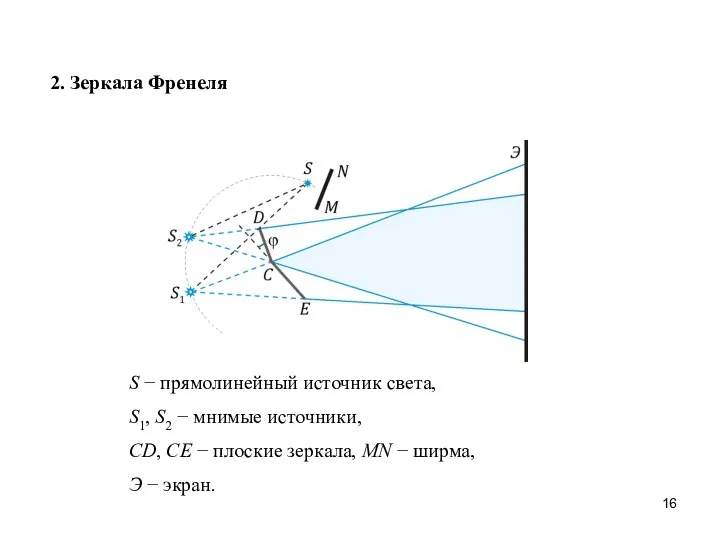
- 16. 2. Зеркала Френеля S − прямолинейный источник света, S1, S2 − мнимые источники, CD, CE −
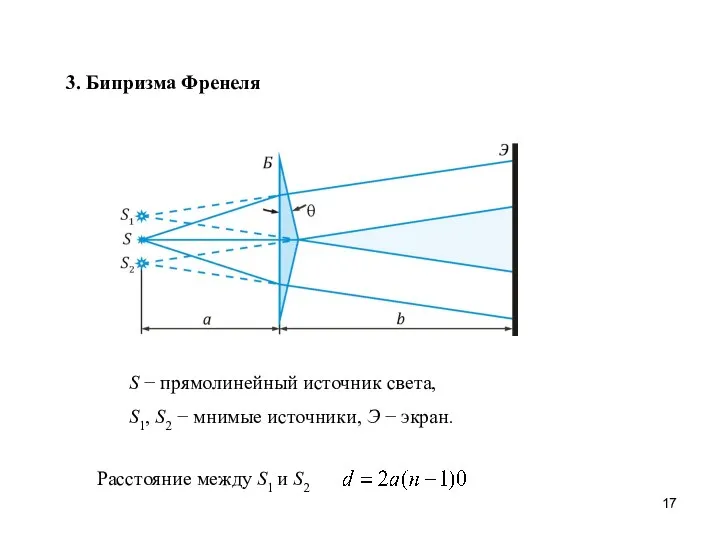
- 17. 3. Бипризма Френеля S − прямолинейный источник света, S1, S2 − мнимые источники, Э − экран.
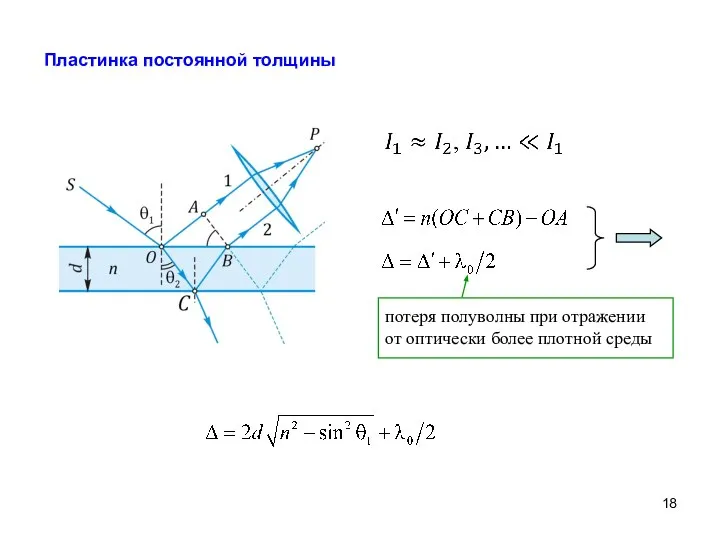
- 18. Пластинка постоянной толщины потеря полуволны при отражении от оптически более плотной среды
- 19. Максимум: Минимум: Условие интерференции:
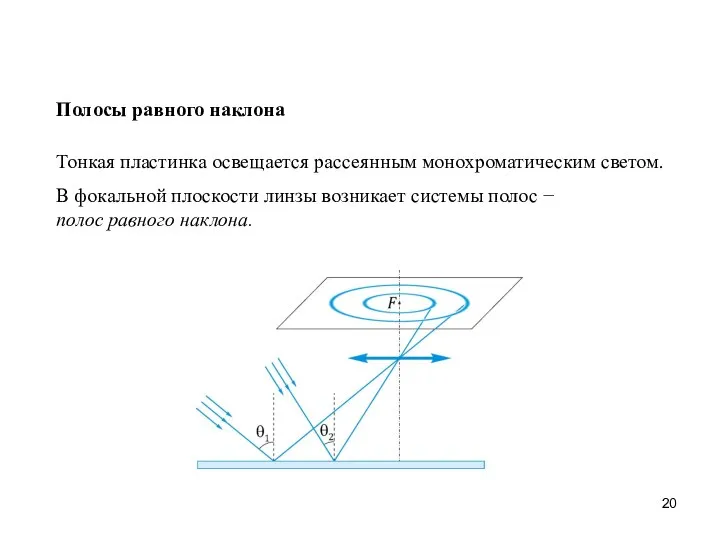
- 20. Полосы равного наклона Тонкая пластинка освещается рассеянным монохроматическим светом. В фокальной плоскости линзы возникает системы полос
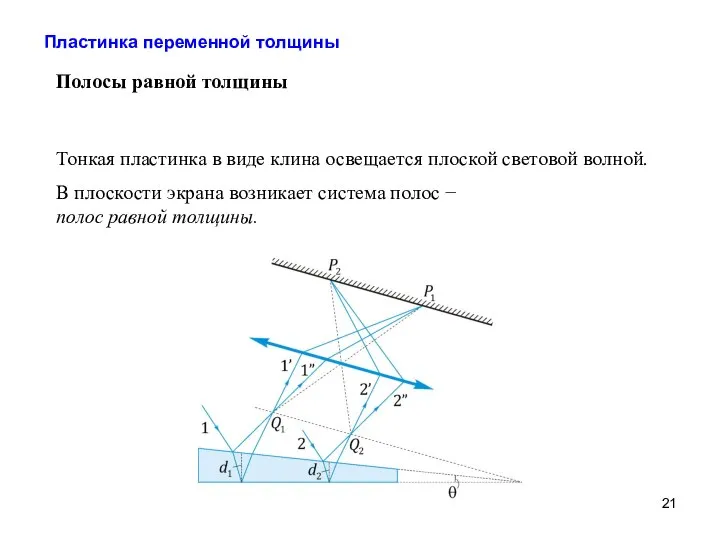
- 21. Полосы равной толщины Тонкая пластинка в виде клина освещается плоской световой волной. В плоскости экрана возникает
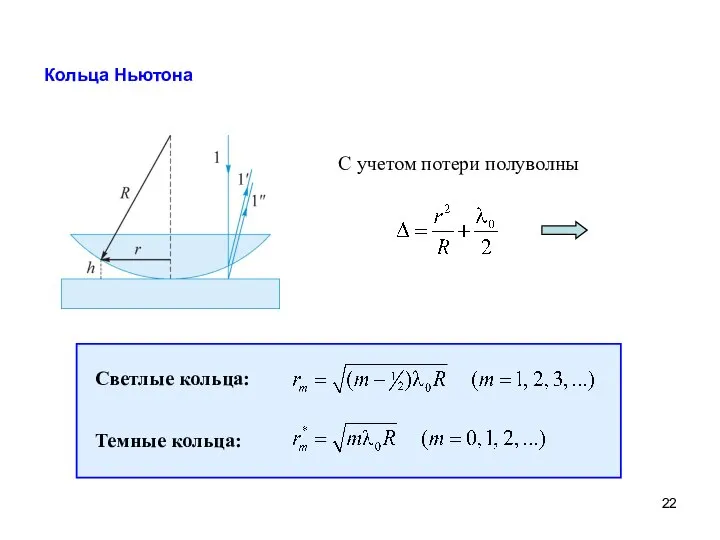
- 22. Кольца Ньютона С учетом потери полуволны Светлые кольца: Темные кольца:
- 24. Скачать презентацию







 Презентация на тему Однофазный мостовой выпрямитель
Презентация на тему Однофазный мостовой выпрямитель  Фиксаторы движущихся деталей или узлов
Фиксаторы движущихся деталей или узлов ВКР: Методика определения глубины максимума ШАЛ по длительности импульса Черенковского излучения
ВКР: Методика определения глубины максимума ШАЛ по длительности импульса Черенковского излучения Явление электромагнитной индукции
Явление электромагнитной индукции Презентация на тему Телевидение
Презентация на тему Телевидение  Входной контроль
Входной контроль Влияние химической связи на свойства материалов
Влияние химической связи на свойства материалов Определение фокусного расстояния линзы. Лабораторная работа
Определение фокусного расстояния линзы. Лабораторная работа Исследование полей Токов смещения
Исследование полей Токов смещения Волшебница вода
Волшебница вода Законы Ньютона
Законы Ньютона Силы в механике. Решение задач. Урок физики в 10 классе
Силы в механике. Решение задач. Урок физики в 10 классе Необычные свойства обычной воды
Необычные свойства обычной воды Равновесие тел
Равновесие тел Основи термодинаміки
Основи термодинаміки Ток проводимости в металлах, его характеристики и условия существования
Ток проводимости в металлах, его характеристики и условия существования Области применения ультрафиолетового и инфракрасного излучений
Области применения ультрафиолетового и инфракрасного излучений Теория гироскопов
Теория гироскопов Звук. Колебательные системы
Звук. Колебательные системы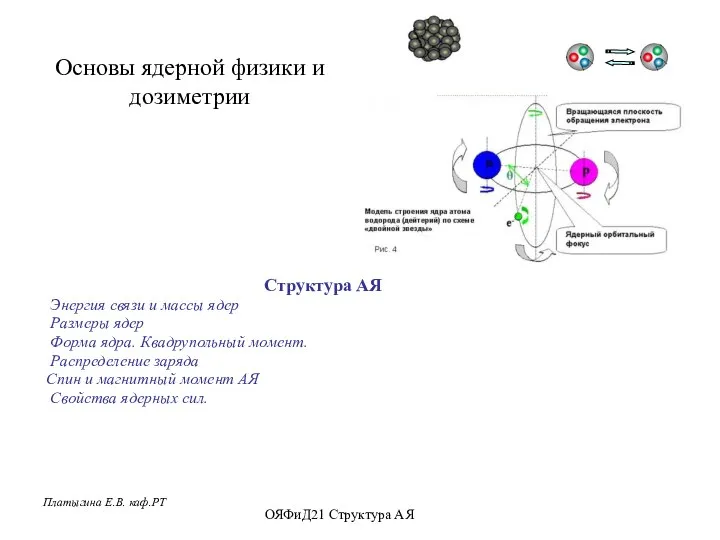 Основы ядерной физики и дозиметрии
Основы ядерной физики и дозиметрии Электрический ток. Соединения проводников
Электрический ток. Соединения проводников Разработка адаптивного метода оценки характеристик досмотровых комплексов с функцией распознавания материалов объектов контроля
Разработка адаптивного метода оценки характеристик досмотровых комплексов с функцией распознавания материалов объектов контроля Электрические цепи. Последовательное и параллельное соединение проводников
Электрические цепи. Последовательное и параллельное соединение проводников Презентация на тему Магнитное поле катушки с током. Электромагниты
Презентация на тему Магнитное поле катушки с током. Электромагниты  Электрическая цепь. Основные законы
Электрическая цепь. Основные законы Автотрансформаторы
Автотрансформаторы Элементарные частицы. Античастицы
Элементарные частицы. Античастицы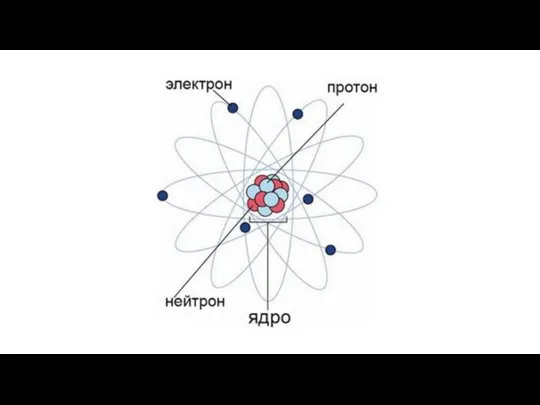 Строение атома
Строение атома