Содержание
- 2. Взаимодействие молекул При анализе свойств реальных газов необходимо учитывать взаимодействие между молекулами газа, а также конечное
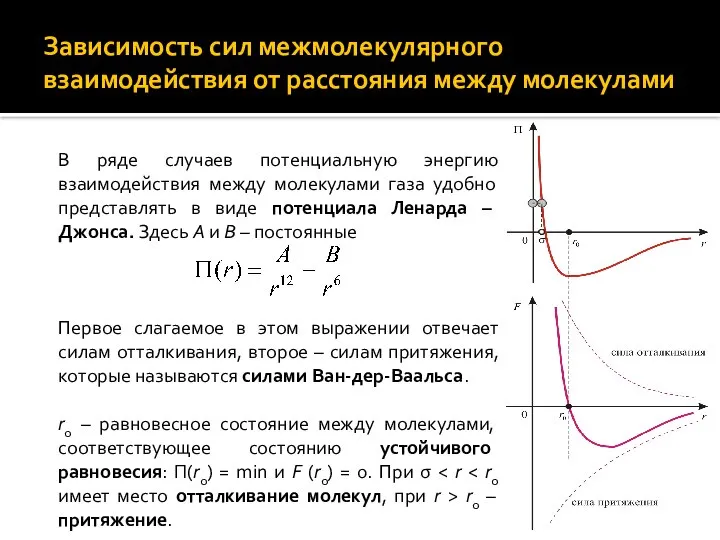
- 3. Зависимость сил межмолекулярного взаимодействия от расстояния между молекулами В ряде случаев потенциальную энергию взаимодействия между молекулами
- 4. Физическая природа сил Ван-дер-Ваальса На больших расстояниях от атома его электрическое поле в целом почто равно
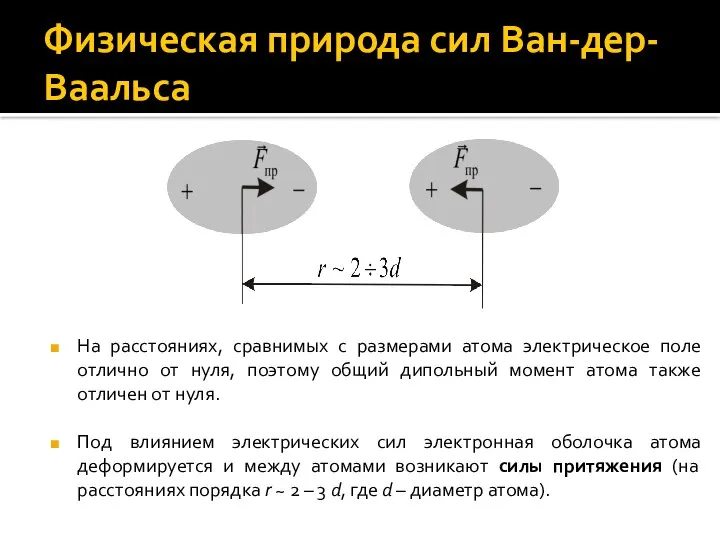
- 5. Физическая природа сил Ван-дер-Ваальса На расстояниях, сравнимых с размерами атома электрическое поле отлично от нуля, поэтому
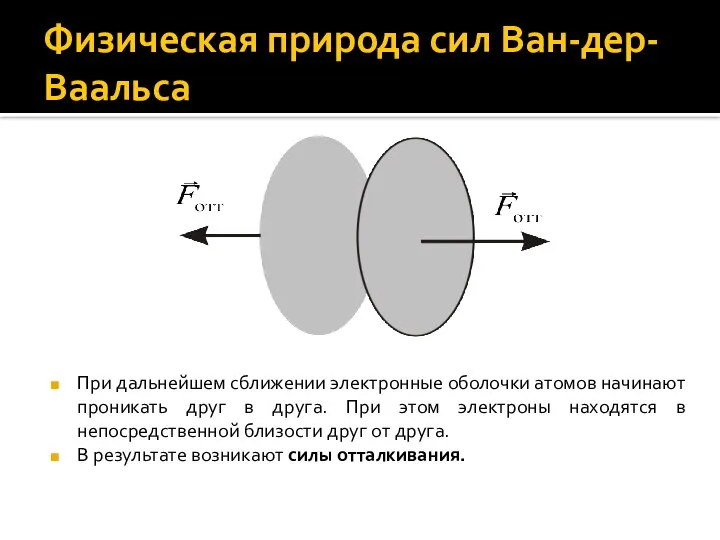
- 6. Физическая природа сил Ван-дер-Ваальса При дальнейшем сближении электронные оболочки атомов начинают проникать друг в друга. При
- 7. Уравнение Ван-дер-Ваальса
- 8. Уравнение Ван-дер-Ваальса Уравнение, описывающее поведение газов в широком интервале давлений и плотностей, было получено Ван-дер-Ваальсом путем
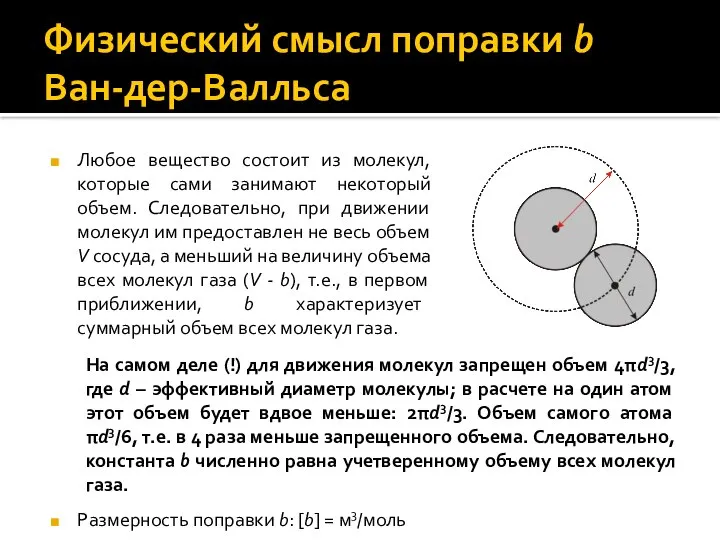
- 9. Физический смысл поправки b Ван-дер-Валльса Любое вещество состоит из молекул, которые сами занимают некоторый объем. Следовательно,
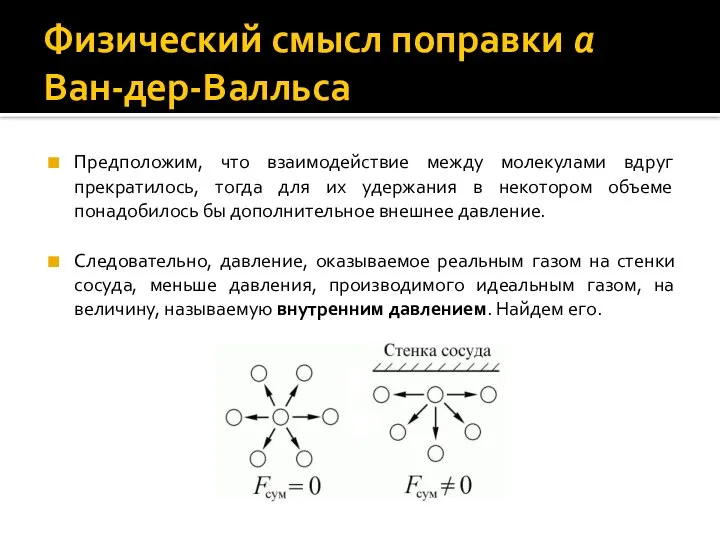
- 10. Физический смысл поправки a Ван-дер-Валльса Предположим, что взаимодействие между молекулами вдруг прекратилось, тогда для их удержания
- 11. Физический смысл поправки a Ван-дер-Валльса Мысленно представим молекулы в виде двух групп 1 и 2. Сила,
- 12. Изотермы Ван-дер-Ваальса
- 13. Изотермы Ван-дер-Ваальса Уравнение Ван-дер-Ваальса для одного моля газа имеет вид После раскрытия скобок это уравнение можно
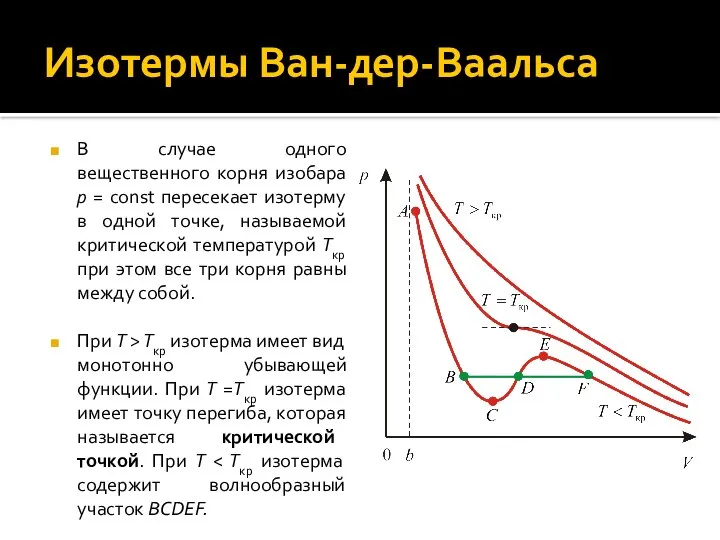
- 14. Изотермы Ван-дер-Ваальса В случае одного вещественного корня изобара p = const пересекает изотерму в одной точке,
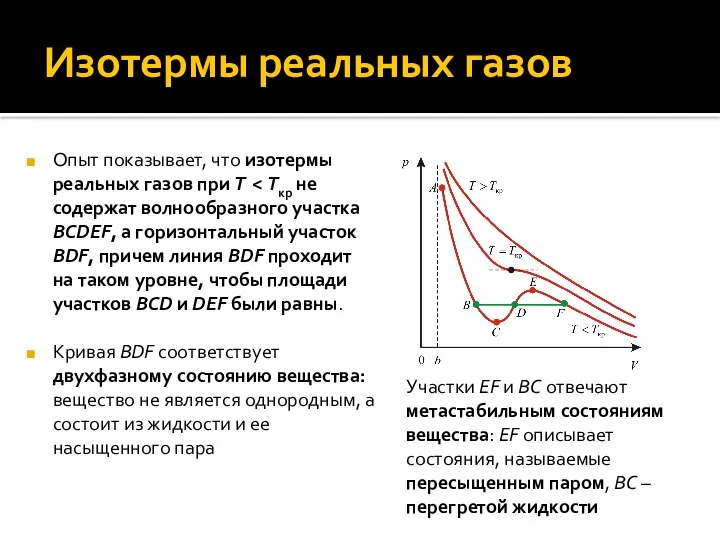
- 15. Изотермы реальных газов Опыт показывает, что изотермы реальных газов при T Кривая BDF соответствует двухфазному состоянию
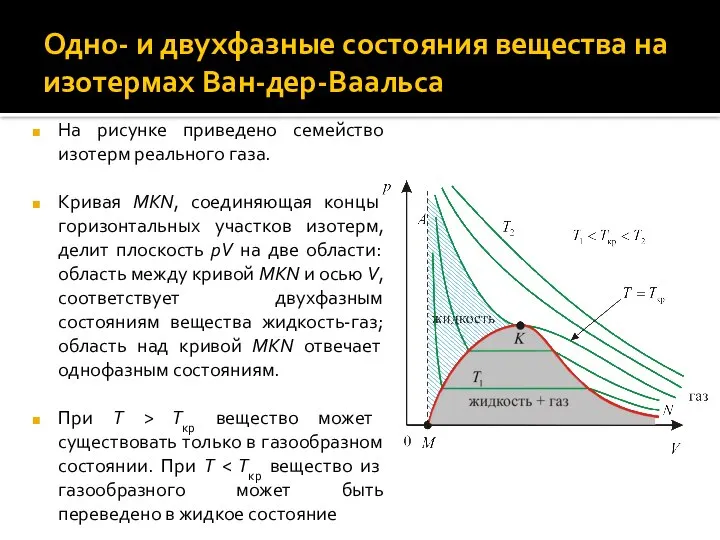
- 16. Одно- и двухфазные состояния вещества на изотермах Ван-дер-Ваальса На рисунке приведено семейство изотерм реального газа. Кривая
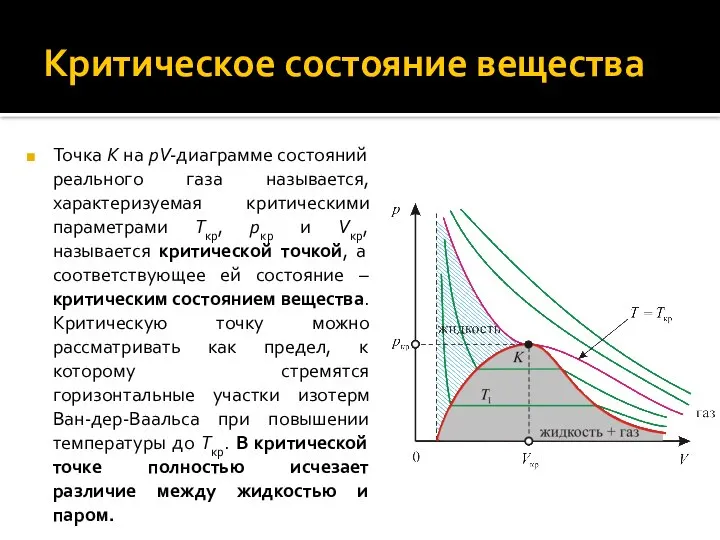
- 17. Критическое состояние вещества
- 18. Критическое состояние вещества Точка K на pV-диаграмме состояний реального газа называется, характеризуемая критическими параметрами Tкр, pкр
- 20. Скачать презентацию








 Закон сохранения энергии
Закон сохранения энергии Сверхпроводи́мость
Сверхпроводи́мость Плавление и отвердевание
Плавление и отвердевание 1435976
1435976 Рассеивающие линзы
Рассеивающие линзы Кинематика. Средняя скорость
Кинематика. Средняя скорость Тезаурус
Тезаурус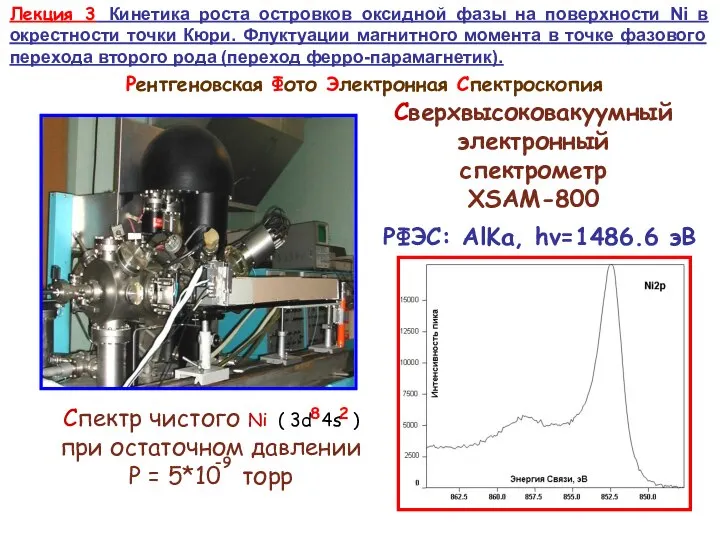 Кинетика роста островков оксидной фазы на поверхности Ni в окрестности точки Кюри
Кинетика роста островков оксидной фазы на поверхности Ni в окрестности точки Кюри Физика и технология наноструктур
Физика и технология наноструктур Вес воздуха. Атмосферное давление
Вес воздуха. Атмосферное давление Электрический ток в металлах. Электрический ток в полупроводниках
Электрический ток в металлах. Электрический ток в полупроводниках Кот Шрёдингера. Коллапс волновой функции. Введение в квантовую физику
Кот Шрёдингера. Коллапс волновой функции. Введение в квантовую физику Тепловые двигатели. Виды двигателей
Тепловые двигатели. Виды двигателей Рычаг. Самостоятельная работа
Рычаг. Самостоятельная работа Ответы на вопросы
Ответы на вопросы Трехфазный переменный ток
Трехфазный переменный ток Презентация урока физики в 8 классе «Параллельное соединение проводников ». Автор: Глазунова Лидия Ивановна, учитель физики МБО
Презентация урока физики в 8 классе «Параллельное соединение проводников ». Автор: Глазунова Лидия Ивановна, учитель физики МБО Частицы с отрицательной энергией в эргосфере чёрных дыр
Частицы с отрицательной энергией в эргосфере чёрных дыр Космические скорости
Космические скорости Определение цены деления измерительного прибора
Определение цены деления измерительного прибора I закон термодинамики
I закон термодинамики Атомное ядро. Нуклонная модель ядра. Изотопы. Энергия связи нуклонов в ядре
Атомное ядро. Нуклонная модель ядра. Изотопы. Энергия связи нуклонов в ядре Мембранные процессы
Мембранные процессы Презентация на тему Опасная инерция
Презентация на тему Опасная инерция  Презентация на тему Механические волны
Презентация на тему Механические волны  Закон всемирного тяготения
Закон всемирного тяготения Неравномерное движение (9 класс)
Неравномерное движение (9 класс) Солнце, воздух и вода – наши лучшие друзья
Солнце, воздух и вода – наши лучшие друзья