Содержание
- 2. Постановка задачи Вычислить свободную энергию ферромагнитной пластинки толщиной .
- 3. Решение определением свободной энергии Для ферромагнетика характерны собственные малые колебания намагниченности относительно равновесного значения , которые
- 4. Собственная энергия В результате для свободной энергии получаем Перейдем от суммирования по к интегрированию, причем речь
- 5. Преобразуем интеграл Волновой вектор Закона дисперсии магнона Значит
- 6. Следовательно Введем подстановку отсюда Обозначим Пусть
- 7. Собирая все воедино, получаем свободную энергию ферромагнитной пластины
- 9. Скачать презентацию






 Закон сохранения импульса. Реактивное движение
Закон сохранения импульса. Реактивное движение Решение задач с помощью законов Ньютона
Решение задач с помощью законов Ньютона Движение и его относительность
Движение и его относительность Решение задач на вычисление значения сопротивления силы тока, напряжения в цепи переменного тока
Решение задач на вычисление значения сопротивления силы тока, напряжения в цепи переменного тока Плоская система сходящихся сил. Момент инерции
Плоская система сходящихся сил. Момент инерции Наблюдения и опыты
Наблюдения и опыты Общие сведения о зубчатых передачах
Общие сведения о зубчатых передачах Презентация на тему Сила тяжести. Вес тела. Сила упругости
Презентация на тему Сила тяжести. Вес тела. Сила упругости  Электрическое освещение бытовых и промышленных объектов
Электрическое освещение бытовых и промышленных объектов Презентация
Презентация Энтропия. Теорема Нернста
Энтропия. Теорема Нернста Прямолинейное равноускоренное движение
Прямолинейное равноускоренное движение Удивительное рядом
Удивительное рядом Механические колебания
Механические колебания Теоретическая механика. Кинематика. (Часть 2)
Теоретическая механика. Кинематика. (Часть 2) Презентация на тему Давление на дне морей и океанов
Презентация на тему Давление на дне морей и океанов  Заточка дереворежущего инструмента
Заточка дереворежущего инструмента Изменение в агрегатных состояний вещества
Изменение в агрегатных состояний вещества Давление в жидкости и газе
Давление в жидкости и газе Кручение. Основные понятия деформации кручения
Кручение. Основные понятия деформации кручения Изучение тепловых явлений. 8 класс
Изучение тепловых явлений. 8 класс Применение ядерной энергии. Развитие ядерной энергетики
Применение ядерной энергии. Развитие ядерной энергетики Виды гидравлических сопротивлений
Виды гидравлических сопротивлений От чего зависит количество одинаковых изображенний в калейдоскопе?
От чего зависит количество одинаковых изображенний в калейдоскопе?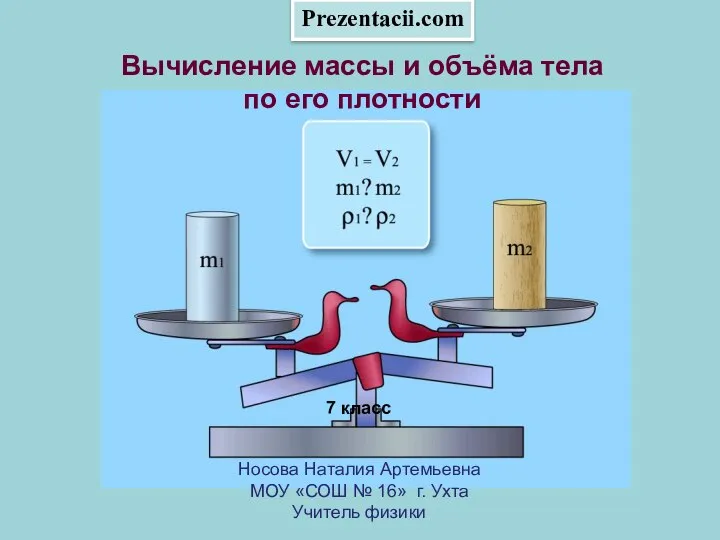 Вычисление массы и объёма тела по его плотности. 7 класс
Вычисление массы и объёма тела по его плотности. 7 класс Энергетическая катастрофа
Энергетическая катастрофа Познавательнотематическое развлечение Течёт река…
Познавательнотематическое развлечение Течёт река… Наука физика
Наука физика