Содержание
- 2. Траектория движения материальной точки – линия, описываемая этой точкой в пространстве. В зависимости от формы траектории
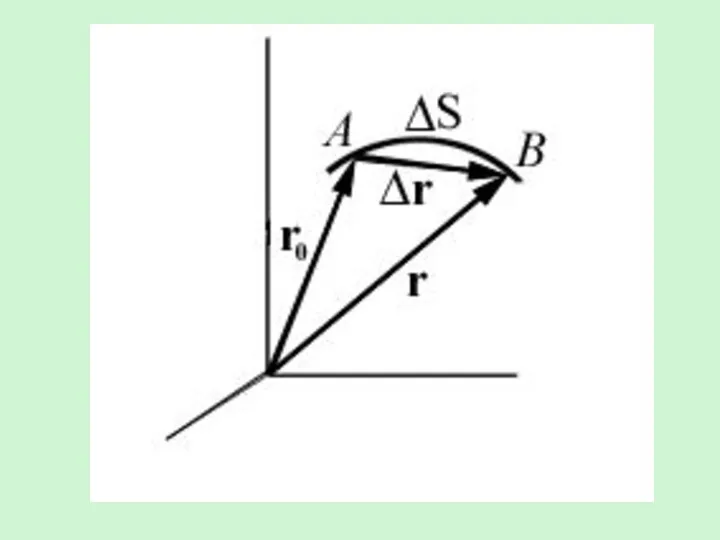
- 4. Вектор , проведенный из начального положения движущейся точки в положение ее в данный момент времени (приращение
- 5. При прямолинейном движении вектор перемещения совпадает с соответствующим участком траектории и модуль перемещения | | равен
- 6. Для характеристики движения материальной точки вводится векторная величина - скорость, которой определяется как быстрота движения, так
- 7. Для характеристики движения материальной точки вводится векторная величина - скорость, которой определяется как быстрота движения, так
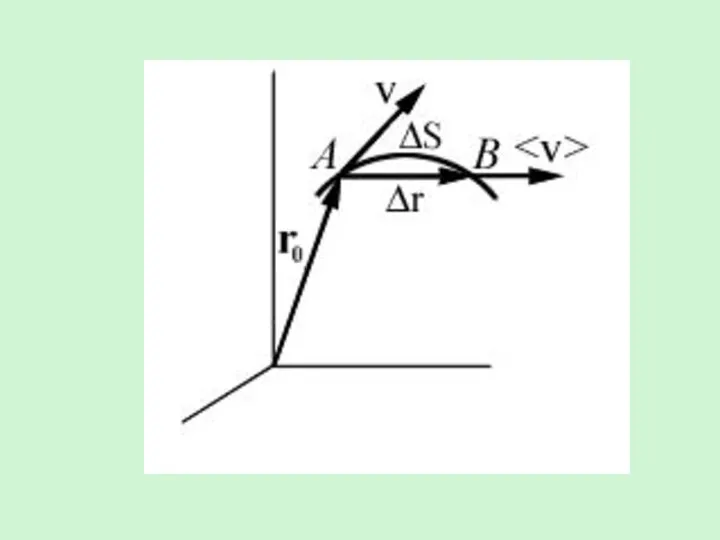
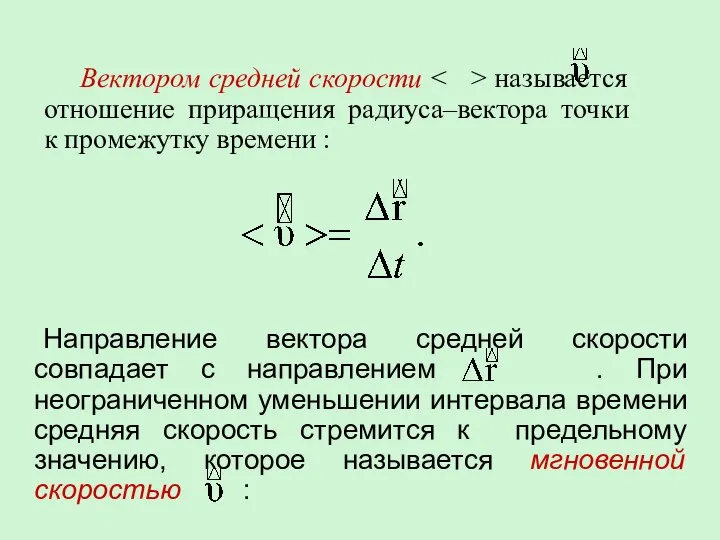
- 9. Направление вектора средней скорости совпадает с направлением . При неограниченном уменьшении интервала времени средняя скорость стремится
- 10. Вектор скорости направлен по касательной к траектории в сторону движения, поэтому модуль мгновенной скорости равен: Мгновенная
- 11. При неравномерном движении модуль мгновенной скорости с течением времени изменяется. В данном случае пользуются скалярной величиной
- 12. Если выражение dS= dt проинтегрировать по времени в пределах от t до t+∆t, то найдем длину
- 13. Длина пути, пройденного точкой за промежуток времени от t1 до t2 дается интегралом:
- 14. Рассмотрим плоское движение. Пусть вектор задает скорость точки А в момент времени t. За время движущаяся
- 15. Средним ускорением неравномерного движения в интервале от t до t+∆t называется векторная величина, равная отношению изменения
- 16. Тангенциальная составляющая ускорения т.е. равна первой производной по времени от модуля скорости, определяя тем самым быстроту
- 17. Полное ускорение тела есть геометрическая сумма тангенциальной и нормальной составляющих:
- 18. Итак, тангенциальная составляющая ускорения характеризует быстроту изменения скорости по модулю (направлена по касательной к траектории), а
- 19. В зависимости от тангенциальной и нормальной составляющих ускорения движение можно классифицировать следующим образом: 1. =0, =0
- 20. Если начальный момент времени t1=0, а начальная скорость то, обозначив t2=t и получим откуда Проинтегрировав эту
- 22. Скачать презентацию
















 Механическое движение. Положение тела в пространстве
Механическое движение. Положение тела в пространстве Механические колебания
Механические колебания opredelenie_koordinaty_dvizh_tela
opredelenie_koordinaty_dvizh_tela Применение скакалки, каната на занятиях физической культуры и внеурочной деятельности
Применение скакалки, каната на занятиях физической культуры и внеурочной деятельности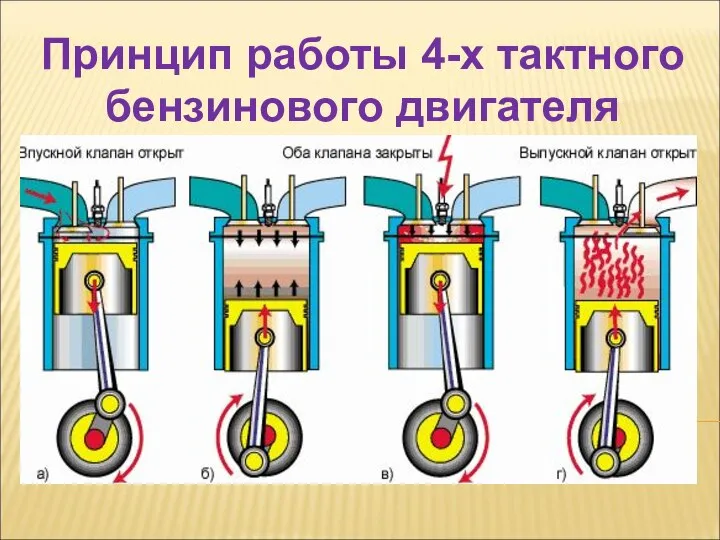 Принцип работы 4-х тактного бензинового двигателя
Принцип работы 4-х тактного бензинового двигателя Оптическое излучение
Оптическое излучение Сравнение количеств теплоты при смешивании воды разной температуры. Лабораторная работа № 1
Сравнение количеств теплоты при смешивании воды разной температуры. Лабораторная работа № 1 Обратимые и необратимые термодинамические процессы. (Лекция 8)
Обратимые и необратимые термодинамические процессы. (Лекция 8) Зависимость давления твердых тел от силы давления и от площади поверхности, на которую действует сила давления
Зависимость давления твердых тел от силы давления и от площади поверхности, на которую действует сила давления Винтовые конвейеры
Винтовые конвейеры Презентация на тему Ядерная модель атома.Квантовые постулаты Бора
Презентация на тему Ядерная модель атома.Квантовые постулаты Бора  Такелажные работы с тросами
Такелажные работы с тросами Устройство и принцип работы дизельного двигателя
Устройство и принцип работы дизельного двигателя Энергия. Виды энергии
Энергия. Виды энергии Время и его измерение. Основы кинематики
Время и его измерение. Основы кинематики Принцип работы 4-х тактного дизельного двигателя
Принцип работы 4-х тактного дизельного двигателя Измерение скоростей молекул газа. Опыт Штерна
Измерение скоростей молекул газа. Опыт Штерна Extended Defects in c-Si
Extended Defects in c-Si Световые явления. 8 класс
Световые явления. 8 класс Термодинамические законы
Термодинамические законы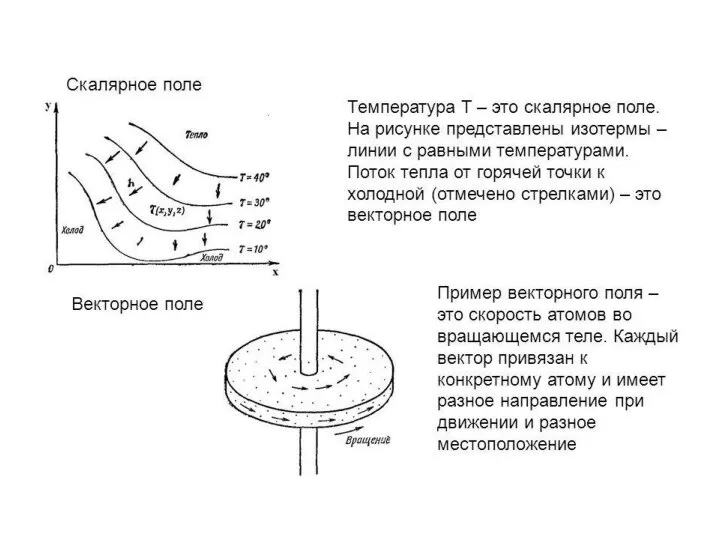 Скалярное поле. Векторное поле
Скалярное поле. Векторное поле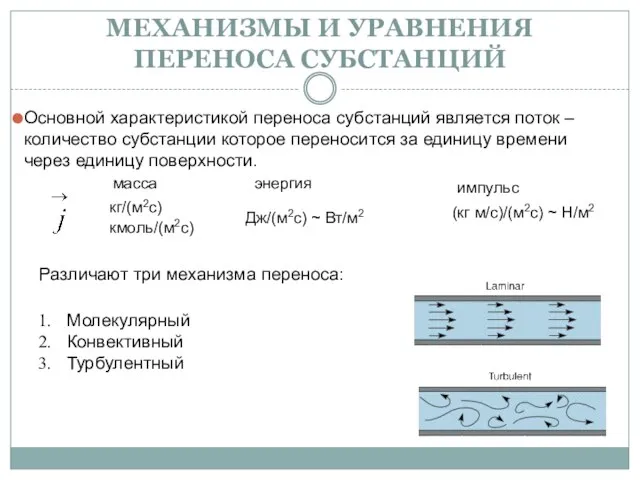 Механизмы и уравнения переноса субстанций
Механизмы и уравнения переноса субстанций Контакт волнистых и шероховатых тел
Контакт волнистых и шероховатых тел 13 июня - День швейной машинки
13 июня - День швейной машинки Надёжность электрических машин. Надёжность контактных колец и подшипниковых узлов электрических машин
Надёжность электрических машин. Надёжность контактных колец и подшипниковых узлов электрических машин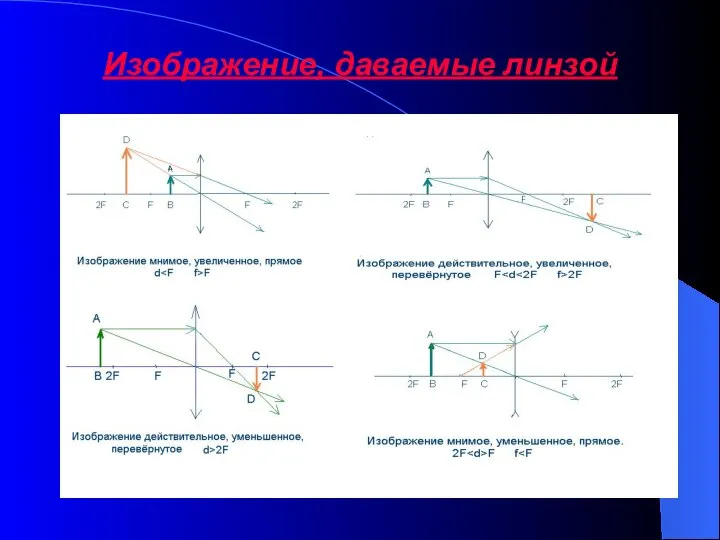 Изображение, даваемые линзой
Изображение, даваемые линзой Свободные и вынужденные колебания. Колебательные системы. (9 класс)
Свободные и вынужденные колебания. Колебательные системы. (9 класс) Плоские и сферические зеркала
Плоские и сферические зеркала