Содержание
- 2. Материальная точка – физическая модель объекта Модель – абстрактная система, являющаяся упрощенной копией реальной системы. Материальная
- 3. Положение материальной точки определяется по отношению к какому-либо другому произвольно выбранному телу. Тело отсчета – условное
- 4. Приборы, служащие для определения положения движущегося тела – линейка и т.п. Прибор, служащий для определения времени
- 5. Тело отсчета, связанная с ним система координат, линейка, часы и приборы для синхронизации часов составляют пространственно-временную
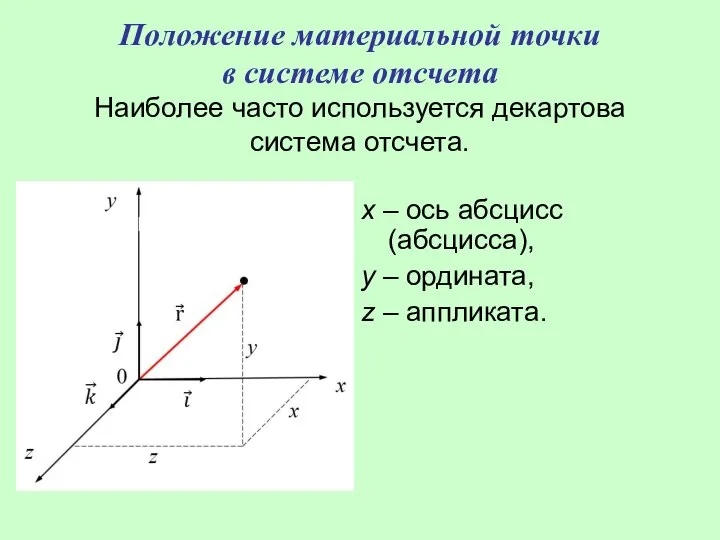
- 6. Положение материальной точки в системе отсчета Наиболее часто используется декартова система отсчета. x – ось абсцисс
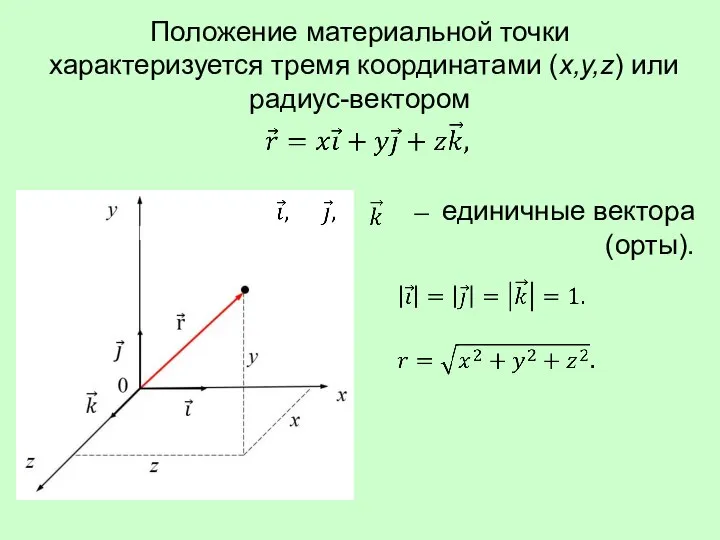
- 7. Положение материальной точки характеризуется тремя координатами (x,y,z) или радиус-вектором единичные вектора (орты).
- 8. При движении материальной точки её координата с течением времени изменяется. Движение материальной точки определяется скалярными уравнениями
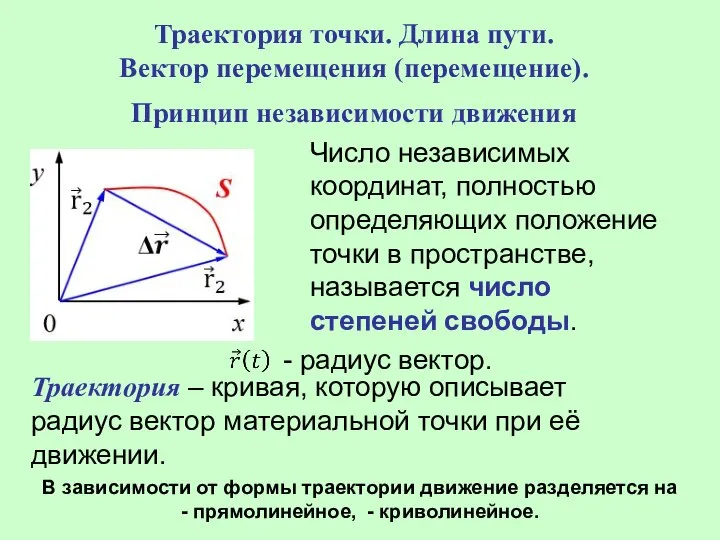
- 9. Траектория точки. Длина пути. Вектор перемещения (перемещение). Принцип независимости движения Число независимых координат, полностью определяющих положение
- 10. Расстояние, отсчитанное вдоль траектории, (длина участка траектории) называется длиной пути S. - скалярная функция. Направленный отрезок
- 11. При прямолинейном движении Если движение происходит в течение бесконечно малого времени Δt → 0, то по
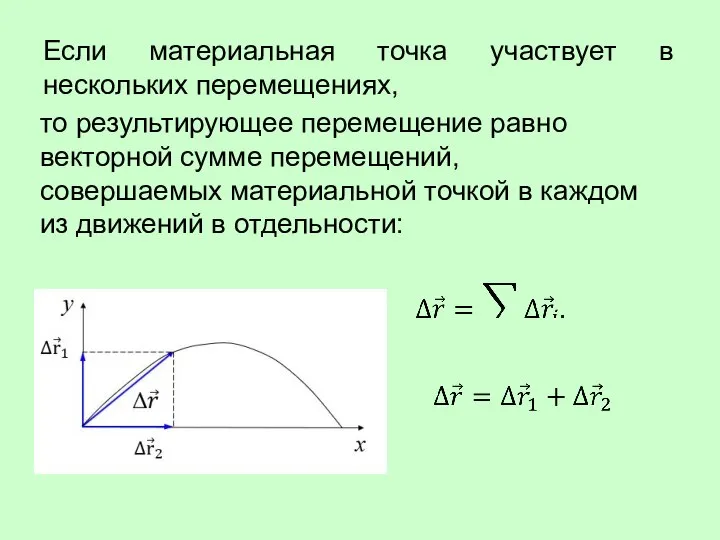
- 12. Если материальная точка участвует в нескольких перемещениях, то результирующее перемещение равно векторной сумме перемещений, совершаемых материальной
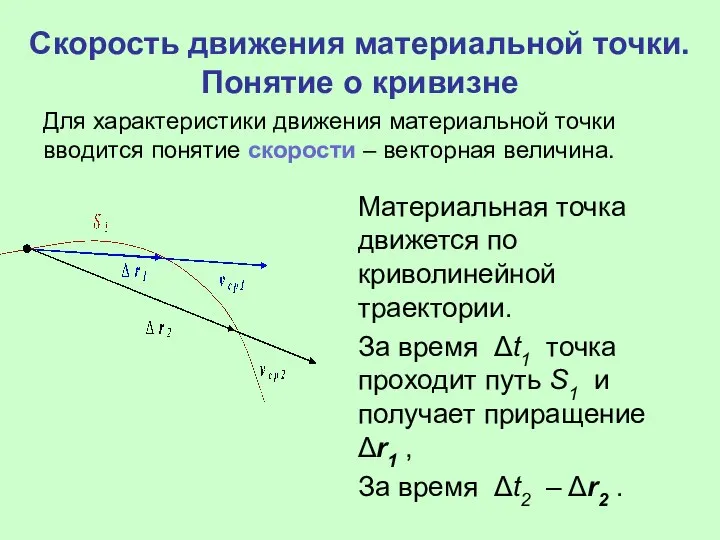
- 13. Скорость движения материальной точки. Понятие о кривизне Материальная точка движется по криволинейной траектории. За время Δt1
- 14. Вектор средней скорости – отношение перемещения к промежутку времени Вектор средней скорости характеризует изменение положения радиус-вектора.
- 15. Мгновенная скорость материальной точки – векторная величина, равная первой производной радиус-вектора движущейся точки по времени. ,
- 16. В математике производной функции в точке x0 называется предел отношения изменения функции Δy в этой точке
- 17. Физический смысл производной: это среднее значение изменения функции на таком интервале, на котором среднее значение функции
- 18. Неравномерное движение Средняя скорость неравномерного движения – скалярная величина. Средняя скорость больше модуля вектора средней скорости.
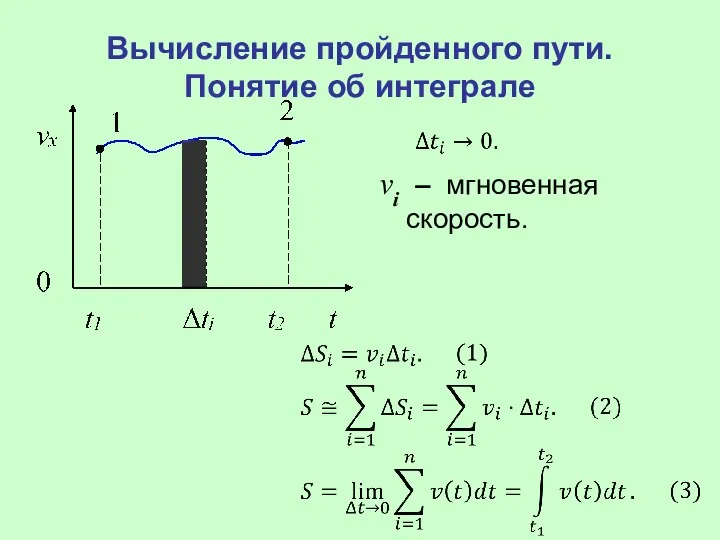
- 19. Вычисление пройденного пути. Понятие об интеграле vi – мгновенная скорость.
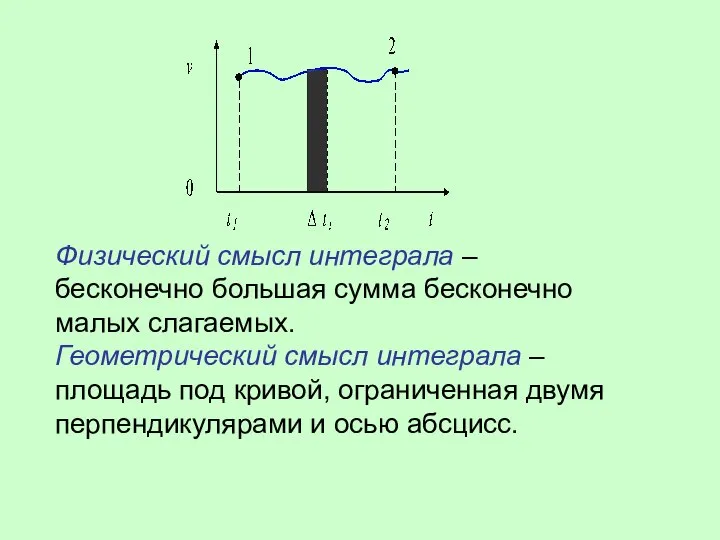
- 20. Физический смысл интеграла – бесконечно большая сумма бесконечно малых слагаемых. Геометрический смысл интеграла – площадь под
- 21. Средняя скорость прохождения пути Средняя скорость неравномерного движения – средняя скорость такого равномерного движения, при котором
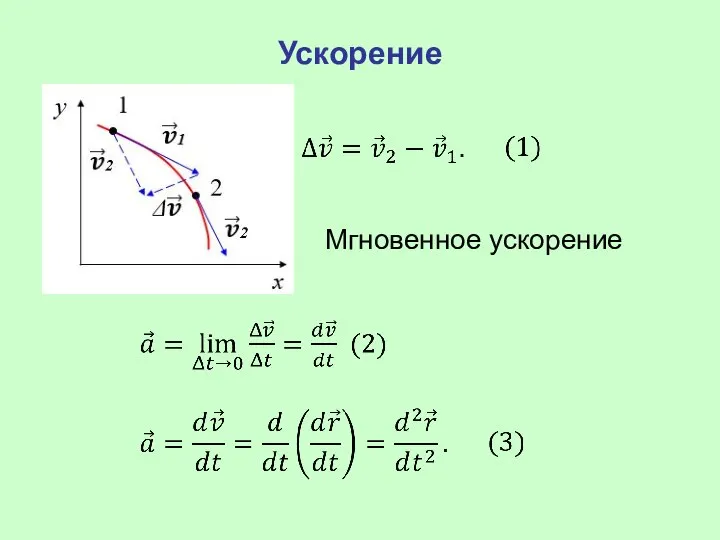
- 22. Ускорение Мгновенное ускорение
- 23. Модуль среднего ускорения: Ускорение движения материальной точки это первая производная от вектора скорости по времени или
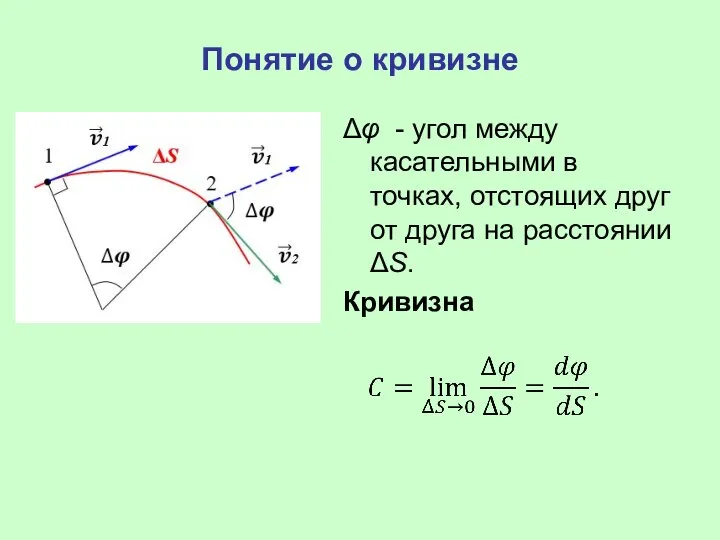
- 24. Понятие о кривизне Δφ - угол между касательными в точках, отстоящих друг от друга на расстоянии
- 25. Кривизна траектории характеризует скорость поворота касательной при движении или степень искривленности кривой. Радиус кривизны траектории в
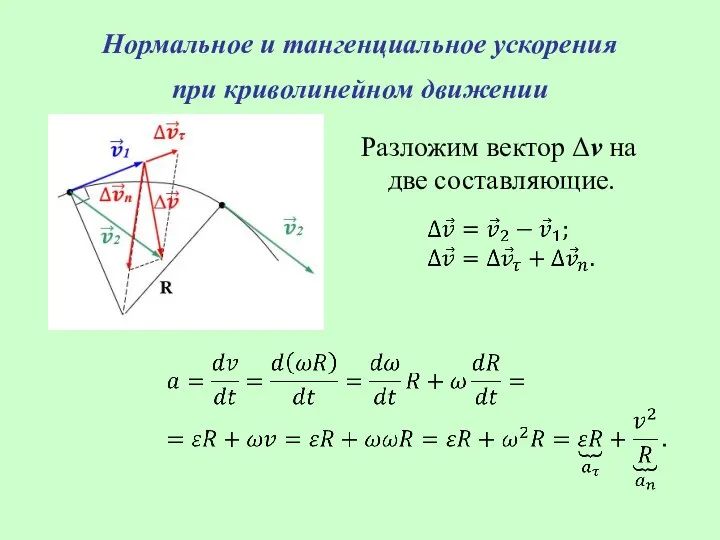
- 26. Нормальное и тангенциальное ускорения при криволинейном движении Разложим вектор Δv на две составляющие.
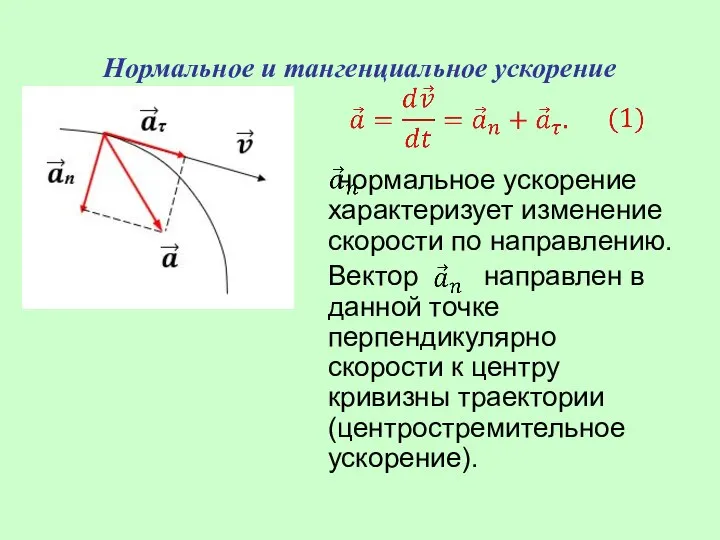
- 27. Нормальное и тангенциальное ускорение нормальное ускорение характеризует изменение скорости по направлению. Вектор направлен в данной точке
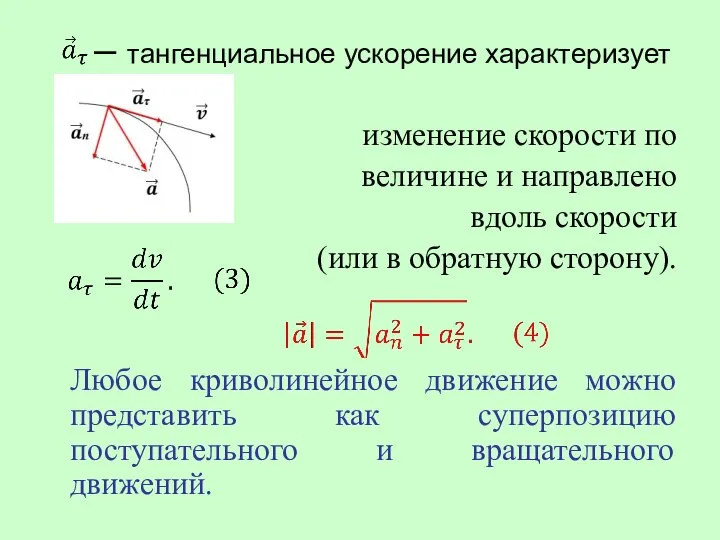
- 28. – тангенциальное ускорение характеризует изменение скорости по величине и направлено вдоль скорости (или в обратную сторону).
- 29. НЕКОТОРЫЕ ВИДЫ ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ
- 30. Основная задача механики (Прямая задача) Состоит в нахождении закона движения – кинематического уравнения. Закон движения –
- 31. Обратная задача механики Определение кинематического уравнения движения по известным характеристикам движения.
- 32. Понятие об абсолютно твердым телом (АТТ). Поступательное и вращательное движение Абсолютно твердое тело – это модель,
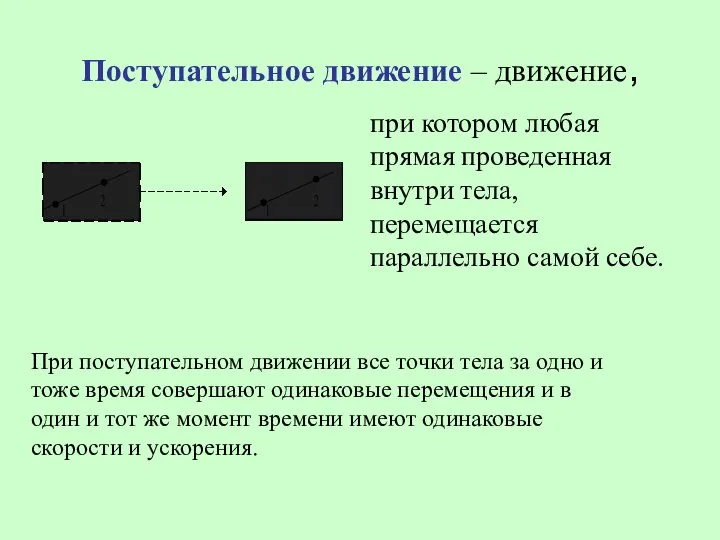
- 33. Поступательное движение – движение, при котором любая прямая проведенная внутри тела, перемещается параллельно самой себе. При
- 34. Абсолютно твердое тело Поступательное движение АТТ можно рассматривать, как движение материальной точки.
- 35. Кинематические уравнения. 1. Равномерное движение материальной точки вдоль оси x. x0 – начальная координата. 2. Равнопеременное
- 36. ЭНЕРГЕТИКА (параграфы 1.1.7, 1.1.8, 3.1 Методического навигатора) Вращающиеся тела представляют большой интерес для энергетиков. Вращаются роторы
- 37. Рабочее колесо турбины Красноярской ГЭС Гидротурбина Рабочее колесо паровой турбины
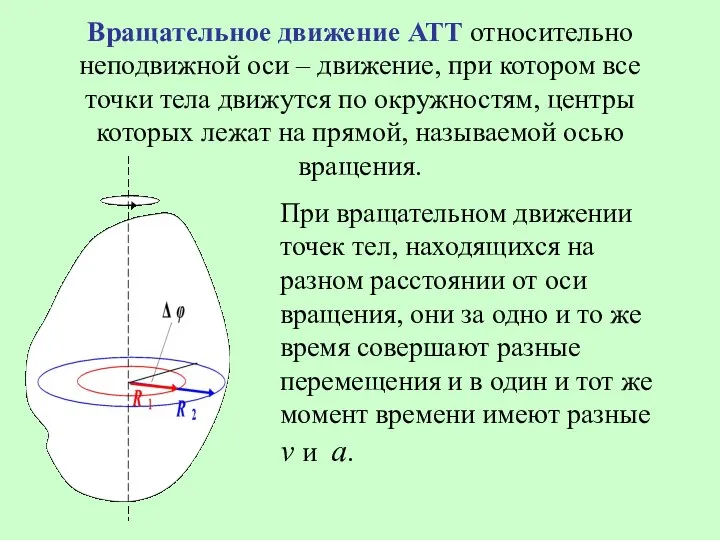
- 38. Вращательное движение АТТ относительно неподвижной оси – движение, при котором все точки тела движутся по окружностям,
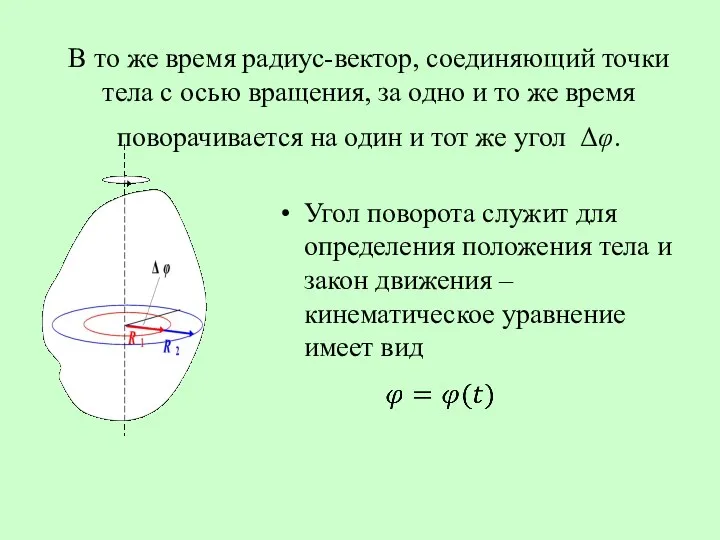
- 39. В то же время радиус-вектор, соединяющий точки тела с осью вращения, за одно и то же
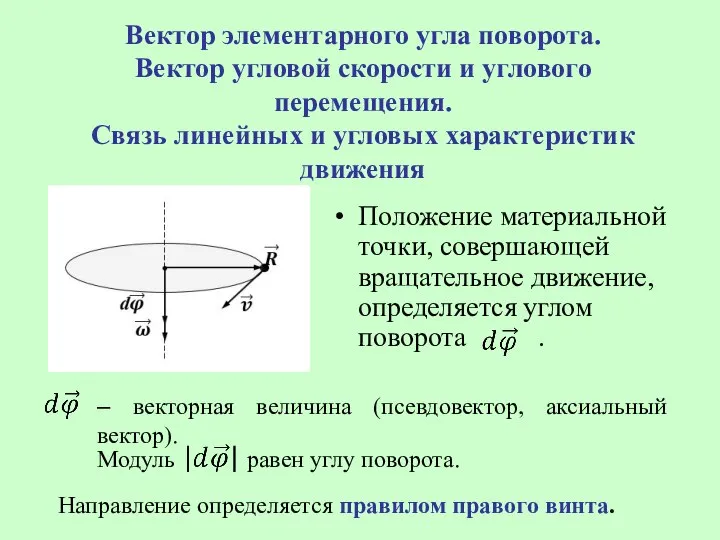
- 40. Вектор элементарного угла поворота. Вектор угловой скорости и углового перемещения. Связь линейных и угловых характеристик движения
- 41. Угловая скорость – векторная величина, равная первой производной угла поворота по времени Линейная скорость точки В
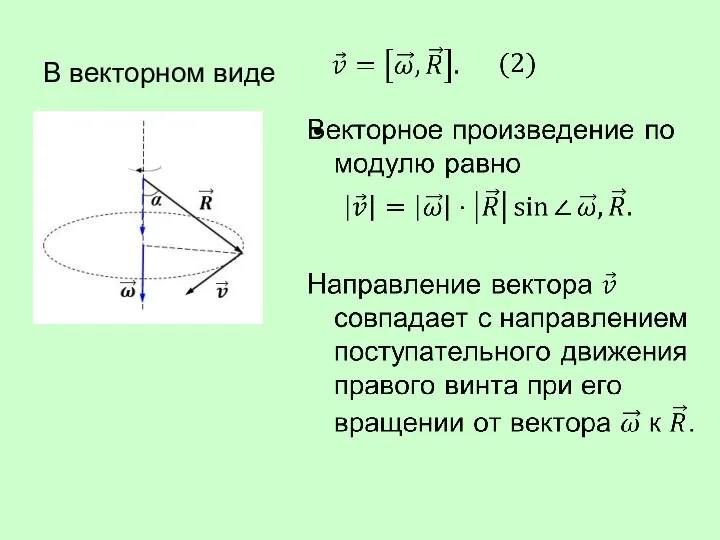
- 42. В векторном виде
- 43. Угловое ускорение – векторная величина, равная первой производной угловой скорости по времени При ускоренном движении при
- 44. Кинематическое уравнение равномерного вращения Частота вращения: Период:
- 45. Кинематическое уравнение равнопеременного вращения Длина пути, пройденного точкой по дуге радиуса R:
- 46. Связь линейных с угловыми величинами
- 47. Скалярное и векторное произведение векторов ● Скалярное произведение: Пример: работа, совершаемая силой
- 49. Скачать презентацию





























 Задача по физике. Задания к открытому уроку математика + физика
Задача по физике. Задания к открытому уроку математика + физика 7_Sily_v_prirode_sila_tyazhesti_ves (1)
7_Sily_v_prirode_sila_tyazhesti_ves (1) Динамика материальной точки. Лекция 3
Динамика материальной точки. Лекция 3 Технічне обслуговування та наладка верстату HAAS EC-400
Технічне обслуговування та наладка верстату HAAS EC-400 Закон Кеплера
Закон Кеплера Электрическое сопротивление
Электрическое сопротивление Работа измерительного прибора ИРК-ПРО
Работа измерительного прибора ИРК-ПРО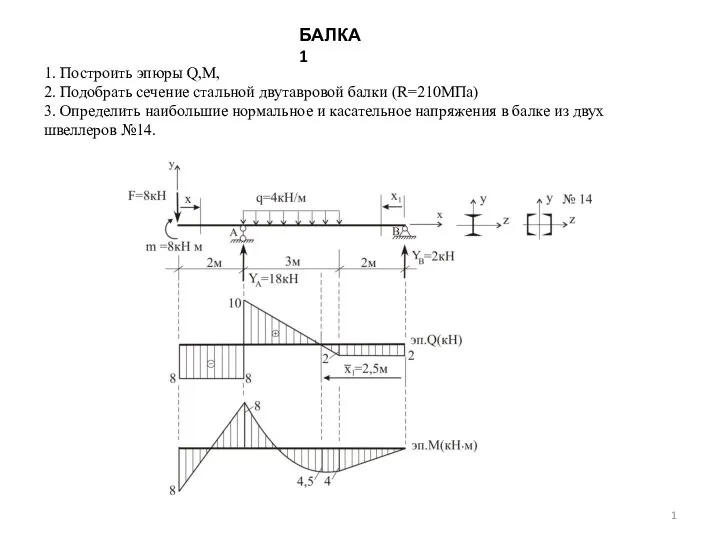 Расчет балки
Расчет балки Физика элементарных частиц
Физика элементарных частиц Электростатика. Электрические взаимодействия
Электростатика. Электрические взаимодействия Свет. Источники света
Свет. Источники света Уравнение неразрывности. Лекция 5
Уравнение неразрывности. Лекция 5 Электрический ток. Источники тока
Электрический ток. Источники тока Ультразвук. Понятие ультразвук
Ультразвук. Понятие ультразвук Полный цикл изготовления телескопов в домашних условиях
Полный цикл изготовления телескопов в домашних условиях Квазистационарное электромагнитное поле
Квазистационарное электромагнитное поле Термоядерный синтез
Термоядерный синтез Конструкция механизма Ланчестера
Конструкция механизма Ланчестера Типы соединений потребителей тока
Типы соединений потребителей тока Презентация на тему Решение задач по физике
Презентация на тему Решение задач по физике  Трение в природе, технике, быту
Трение в природе, технике, быту Термодинамическая работа
Термодинамическая работа Развитие представлений о строении атома. Модель резерфорда
Развитие представлений о строении атома. Модель резерфорда Упругие свойства среды. Лекция 1.13
Упругие свойства среды. Лекция 1.13 ВКР: Метод инфракрасной спектроскопии в целях судебной пожарно-технической экспертизы
ВКР: Метод инфракрасной спектроскопии в целях судебной пожарно-технической экспертизы Расчет амплитудно-частотных характеристик фильтров
Расчет амплитудно-частотных характеристик фильтров Волокна большого диаметра. Анализ фазового состава, макро- и микроструктуры полуфабрикатов и готовых изделий из B-Al
Волокна большого диаметра. Анализ фазового состава, макро- и микроструктуры полуфабрикатов и готовых изделий из B-Al Май күпдеші озған өткізгіш материал және оның парамтрі
Май күпдеші озған өткізгіш материал және оның парамтрі