Лекция 2. Резьбовые соединения

Общие положения
Детали машин
Резьбовые соединения являются наиболее распростра-ненными разъемными соединениями. Их образуют болты, винты, шпильки, гайки и другие детали, снабженные резьбой.
Резьба образуется путем нанесения на поверхность деталей винтовых канавок, форма которых соответствует профилю резьбы.
По форме поверхности детали различают цилиндрические и конические резьбы.
По форме профиля различают треугольные, прямоуголь-ные, трапецеидальные, круглые и другие резьбы.
В зависимости от направления винтовой линии различают правые и левые резьбы. Преимущественно используют правую резьбу, левая резьба применяется только в специальных случаях.

Классификация резьб по назначению
Детали машин
В зависимости от назначения резьбы делят на крепежные, крепежно-уплотняющие и ходовые.
Крепежные резьбы применяют для скрепления деталей. Они имеют треугольный профиль, отличающийся повышенным моментом сопротивления отвинчиванию и высокой прочностью.
Крепежно-уплотняющие резьбы применяют для скрепления деталей в соединениях, требующих герметичности. Они также имеют треугольный профиль, но без зазоров в сопряжении болта и гайки.
Ходовые резьбы используют в механизмах для преобра-зования вращательного движения в поступательное и наоборот.

Метрические резьбы
Детали машин
Основной крепежной резьбой является метрическая резьба. Профиль резьбы представляет собой равносторонний треугольник с углом профиля α =60°. Различают метрические резьбы с крупным и мелким шагом. Преимущественно применяют метрические резьбы с крупным шагом, поскольку они прочнее, менее чувствительны к изнашиванию и неточностям изготовления.
Резьбы с мелким шагом применяются при действии переменных нагрузок, для тонкостенных деталей и в регулировочных устройствах. Метрическую резьбу с крупным шагом обозначают буквой М и числом, обозначающим номинальный диаметр резьбы в мм, например М20. Для метрической резьбы с мелким шагом допол-нительно указывают шаг, например М20х2.

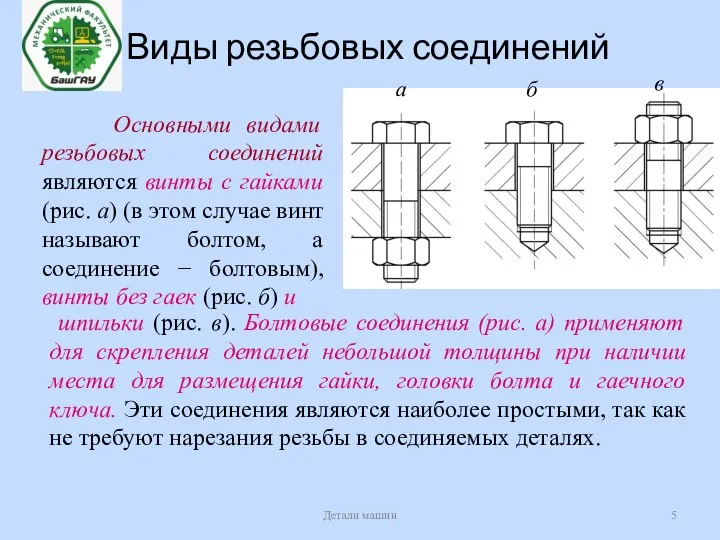
Виды резьбовых соединений
Детали машин
Основными видами резьбовых соединений являются винты с гайками (рис. а) (в этом случае винт называют болтом, а соединение − болтовым), винты без гаек (рис. б) и
шпильки (рис. в). Болтовые соединения (рис. а) применяют для скрепления деталей небольшой толщины при наличии места для размещения гайки, головки болта и гаечного ключа. Эти соединения являются наиболее простыми, так как не требуют нарезания резьбы в соединяемых деталях.
а
б
в

Виды резьбовых соединений
Детали машин
Винтовые соединения применяют при достаточной толщине детали для размещения резьбового отверстия, а также при отсутствии места для размещения гайки.
Шпильки применяют в тех же случаях, что и винты, если материал соединяемых деталей не обеспечивает достаточной прочности резьбы при частых разборках и сборках соедине-ния. Глубину завинчивания l1 в тело детали
принимают из условия равнопрочности тела винта и резьбы: для стальных деталей l1=(1…1,25)d, для чугунных деталей l1 = (1,25…1,5)d.

Геометрические параметры резьбы
Детали машин
Основными геометричес-кими параметрами цилин-дрической резьбы являются (см. рис.): d − номинальный диаметр резьбы; d1 − внут-ренний диаметр резьбы; d2 − средний диаметр резьбы;
p − шаг (расстояние между одноименными сторонами соседних профилей, измеренное в направлении оси резьбы); ph − ход (перемещение винта вдоль своей оси при повороте на один оборот в неподвижной гайке); α − угол профиля резьбы; ψ − угол подъема резьбы. Для однозаходных резьб ph = p. Для многозаходных резьб
ph = np, где n − число заходов.

Основные типы резьб.
Метрические резьбы
Детали машин
Основной крепежной резьбой является метрическая резьба. Профиль резьбы представляет собой равносторонний треугольник с углом профиля α =60°. Различают метрические резьбы с крупным и мелким шагом. Преимущественно применяют метрические резьбы с крупным шагом, поскольку они прочнее, менее чувствительны к изнашиванию и неточностям изготовления.
Резьбы с мелким шагом применяются при действии переменных нагрузок, для тонкостенных деталей и в регулировочных устройствах. Метрическую резьбу с крупным шагом обозначают буквой М и числом, обозначающим номинальный диаметр резьбы в мм, например М20. Для метрической резьбы с мелким шагом допол-нительно указывают шаг, например М20х2.

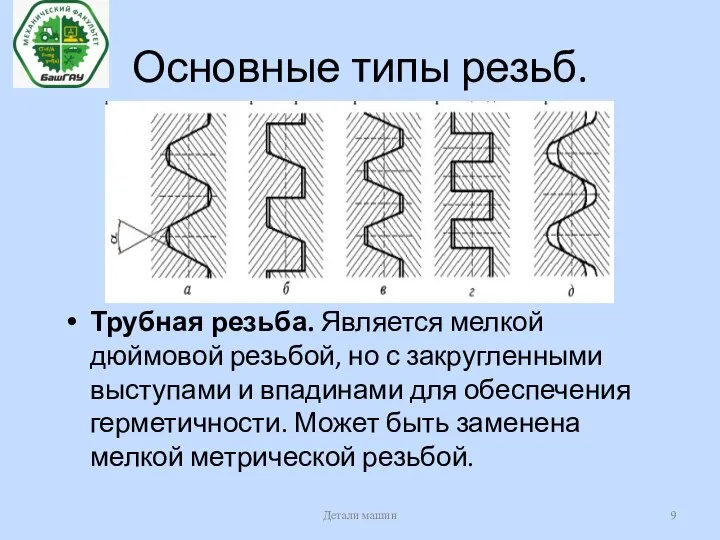
Основные типы резьб.
Трубная резьба. Является мелкой дюймовой резьбой, но с закругленными выступами и впадинами для обеспечения герметичности. Может быть заменена мелкой метрической резьбой.
Детали машин

Основные типы резьб.
Упорная резьба (рис. б). Имеет профиль в виде неравнобочной трапеции с углом α=270 . Применяют в передачах винт–гайка при больших односторонних осевых нагрузках. Закругление впадин повышает динамическую прочность винта. Малый угол наклона (3 градуса) упорной стороны профиля резьбы понижает потери на трение в сравнении с трапецеидальной резьбой.
Круглая резьба (рис. д). Профиль резьбы состоит из дуг, сопряженных короткими прямыми линиями.. Применяют ограниченно (при тяжелых условиях в загрязненной среде).
Детали машин

Основные типы резьб
Трапецеидальная резьба (рис. в). Это основная резьба в передаче винт–гайка. Её профиль – равнобочная трапеция с углом α=30 . Применяют для передачи реверсивного движения под нагрузкой.
Прямоугольная резьба (рис. г). Профиль резьбы – квадрат. Обладает пониженной прочностью. Применение ограничено (в малонагруженных передачах винт–гайка).
Детали машин

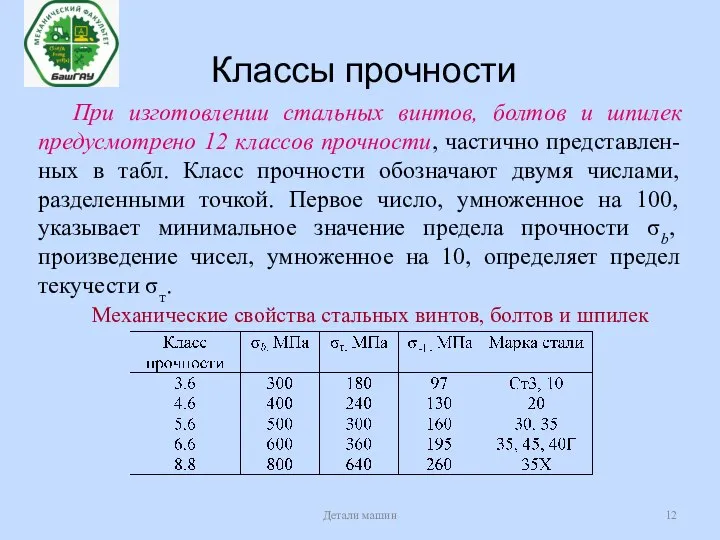
Классы прочности
Детали машин
При изготовлении стальных винтов, болтов и шпилек предусмотрено 12 классов прочности, частично представлен-ных в табл. Класс прочности обозначают двумя числами, разделенными точкой. Первое число, умноженное на 100, указывает минимальное значение предела прочности σb, произведение чисел, умноженное на 10, определяет предел текучести σт.
Механические свойства стальных винтов, болтов и шпилек

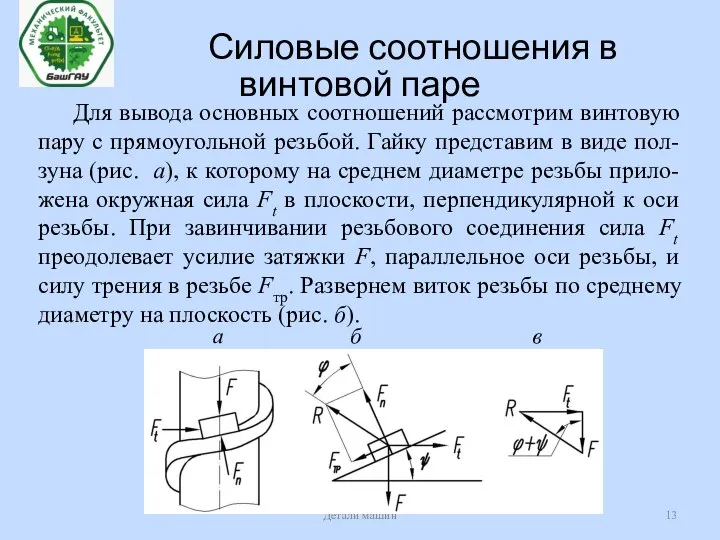
Силовые соотношения в винтовой паре
Детали машин
Для вывода основных соотношений рассмотрим винтовую пару с прямоугольной резьбой. Гайку представим в виде пол-зуна (рис. а), к которому на среднем диаметре резьбы прило-жена окружная сила Ft в плоскости, перпендикулярной к оси резьбы. При завинчивании резьбового соединения сила Ft преодолевает усилие затяжки F, параллельное оси резьбы, и силу трения в резьбе Fтр. Развернем виток резьбы по среднему диаметру на плоскость (рис. б).
а б в

Силовые соотношения
в винтовой паре
Детали машин
Сила трения Fтр по закону Кулона пропорциональна силе нормального давления Fn между ползуном и наклонной плоскостью Fтр = f Fn, где f – коэффициент трения в резьбе. Реакция наклонной плоскости R отклонена от силы Fn на угол трения φ = arctg f. При завинчивании соединения ползун дол-жен находиться в состоянии равновесия под действием трех сил Ft, Fn и R. Из силового треугольника (рис. в) найдем неиз-вестную силу Ft:
Ft = F tg (φ + ψ).
Для перехода к предельным значениям угол трения φ следует заменить приведенным углом трения φ’= arctg f’, где f’ – приведенный коэффициент трения, f’ = f / cos (α/2).

Условия самоторможения резьбы
Детали машин
Для метрической резьбы приведенный угол трения φ’ изменяется в зависимости от коэффициента трения в пределах от 6º (при f ≈ 0,1) до 13º (при f ≈ 0,2). Угол подъема резьбы лежит в диапазоне ψ = 2º30’…3º30’. Следовательно, условие самоторможения ψ < φ’ выполняется. Все крепежные резьбы удовлетворяют условию самоторможения.
Однако практика эксплуатации резьбовых соединений показывает, что при переменных нагрузках и вибрациях воз-можно существенное снижение коэффициента трения на контактных поверхностях и самоотвинчивание гаек и винтов за счет взаимных микросмещений поверхностей трения. Для повышения надежности резьбовых соединений необходимо предохранять их от самоотвинчивания с использованием различных способов стопорения.

Распределение осевой нагрузки
между витками резьбы
Детали машин
Осевая нагрузка с винта на гайку передается через витки резьбы. За счет деформации винта и гайки нагрузка неравномерно распределяется по виткам резьбы. Наиболее нагруженным витком является ближайший к опорной поверхности гайки. Задача о распределении нагрузки по виткам резьбы является статически неопределимой.
Ее решение впервые получено Н. Е. Жуковским, который дополнил урав-нения равновесия сил, приложенных к виткам, условием совместности деформаций винта и гайки. Результа-ты этого решения применительно к стандартной шестивитковой гайке высотой H = 0,8d приведены на рис.

Распределение осевой нагрузки
между витками резьбы
Детали машин
Нижний виток воспринимает 34% общей осевой нагрузки, в то время как последний шестой виток только 7%. Отсюда следует, что увеличение числа витков гайки является малоэф-фективным, поскольку дальние от опорной поверхности витки передают слишком малую часть общей осевой нагрузки. Так, для гайки с 10 витками последний виток передает нагрузку меньше 1% от F.
Экспериментально установлено, что разрушение резьбо-вых соединений, нагруженных переменными нагрузками, происходит в зоне наибольшей концентрации напряжений у наиболее нагруженного витка резьбы.

Лекция 3.
Резьбовые соединения
Расчет незатянутого болтового соединения, нагруженного внешней осевой силой
Расчет затянутого болтового соединения, не нагруженного внешней осевой силой
Расчет затянутого болтового соединения, нагруженного внешней осевой силой
Расчет болтового соединения, нагруженного силами, сдвигающими детали в стыке
Расчет болтов при эксцентричном приложении нагрузки
Расчет группы болтов
Клеммовые соединения
Детали машин

Расчеты на прочность
Детали машин
Основными видами разрушения резьбовых изделий явля-ются: разрыв резьбовой части стержня при действии осевой силы и срез витков резьбы. Стандартные винты, болты и шпильки выполняют равнопрочными на разрыв стержня по резьбе и на срез витков резьбы. Поэтому расчет на прочность резьбового соединения производят по основному критерию − прочности резьбовой части стержня на растяжение.
Допускаемые напряжения выбирают в зависимости от пре-дела текучести материала винта по формуле
[σ] = σТ / [S],
где [S] − коэффициент запаса прочности.
При неконтролируемой затяжке [S] принимают в диапазоне 1.6…5, меньшие значения соответствуют большим диаметрам. Ниже рассмотрены основные случаи расчета резьбовых сое-динений.

Расчет незатянутого болтового соединения, нагруженного
внешней осевой силой
Детали машин
Принимают, что опасное поперечное сечение болта имеет диаметр, равный внутреннему диаметру резьбы d1. Условие прочности болта в опасном сечении имеет вид
где F − осевая сила, Н.
Отсюда определяют расчетное значение внутреннего диаметра резьбы
где Qр − усилие, растягивающее болт, Qр = Fзат.
Полученную величину d1 округляют до ближайшего боль-шего значения, соответствующего стандартной резьбе.
(1)

Расчет незатянутого болтового соединения, нагруженного
внешней осевой силой
Примером служит резьбовой участок крюка для подвешивания груза. Опасным является сечение, ослабленное резьбой. Площадь этого сечения определяется по внутреннему диаметру резьбы
А = πd12/4.
Условие прочности по напряжениям растяжения в стержне
σ = F/[(π/4)d12] ≤ [σ].
Детали машин

Расчет затянутого болтового соединения, не нагруженного внешней осевой силой
Детали машин
При затяжке соединения болт испытывает растяжение и кручение. Напряжение растяжения от усилия затяжки F:
Напряжение кручения от момента сопротивления в резьбе
где Tр − момент сопротивления в резьбе; Wp − полярный момент сопротивления, Wp = πd13/16.
Эквивалентные напряжения найдем по энергетической тео-рии прочности

Расчет затянутого болтового соединения, не нагруженного внешней осевой силой
Вычисления показывают, что для стандартных метрических резьб
σэк ≈ 1,3σ.
Это позволяет рассчитывать прочность болтов по упрощённой формуле
σэк = 1,3Fзат/[(π/4)d12] ≤ [σ].
Детали машин

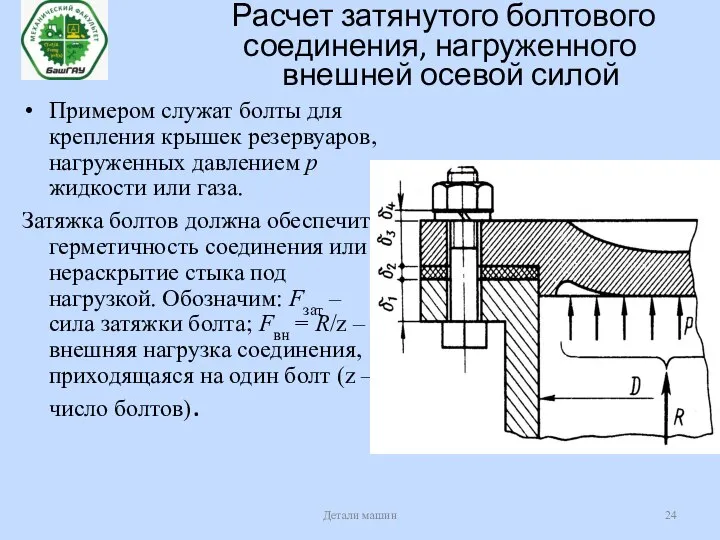
Расчет затянутого болтового соединения, нагруженного внешней осевой силой
Примером служат болты для крепления крышек резервуаров, нагруженных давлением р жидкости или газа.
Затяжка болтов должна обеспечить герметичность соединения или нераскрытие стыка под нагрузкой. Обозначим: Fзат – сила затяжки болта; Fвн = R/z – внешняя нагрузка соединения, приходящаяся на один болт (z – число болтов).
Детали машин

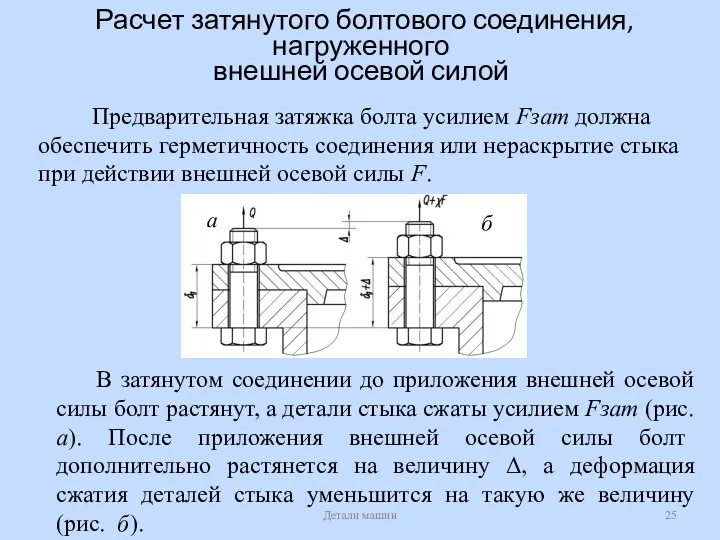
Расчет затянутого болтового соединения, нагруженного
внешней осевой силой
Детали машин
Предварительная затяжка болта усилием Fзат должна обеспечить герметичность соединения или нераскрытие стыка при действии внешней осевой силы F.
a
б
В затянутом соединении до приложения внешней осевой силы болт растянут, а детали стыка сжаты усилием Fзат (рис. а). После приложения внешней осевой силы болт дополнительно растянется на величину Δ, а деформация сжатия деталей стыка уменьшится на такую же величину (рис. б).

Расчет затянутого болтового соединения, нагруженного
внешней осевой силой
Детали машин
Условие совместности деформаций болта и деталей стыка запишем в виде
Δ = λб (F – Fр) = λдFр,
где λб − податливость болта, равная его удлинению при действии единичной нагрузки; λд − податливость деталей стыка.
Отсюда найдем χ = λд/(λб+ λд).
Если обозначим χ коэффициент внешней нагрузки (учитывает приращение нагрузки болта от силы Fвн), то дополнительная нагрузка равна χFвн.
Учитывая кручение стержня болта в процессе затяжки от момента трения в резьбе, расчётная нагрузка болта
Fp = 1,3Fзат + χFвн.
Значение χ = 0,2…0,3 для соединений без мягких прокладок.

Расчет затянутого болтового соединения, нагруженного
внешней осевой силой
При известном значении Fвн силу затяжки принимают
Fзат = КзатFвн,
где Кзат – коэффициент затяжки.
Значения коэффициента затяжки принимают:
- по условию нераскрытия стыка: при постоянной нагрузке Кзат = 1,25…2, при переменной нагрузке Кзат = 2,5…4;
- по условию герметичности: при мягкой прокладке
Кзат = 1,3…2,5, при металлической фасонной прокладке
Кзат = 2…3,5, при металлической плоской прокладке
Кзат = 3…5.
Условие прочности болта
σ = Fр/[(π/4)d12] ≤ [σ].

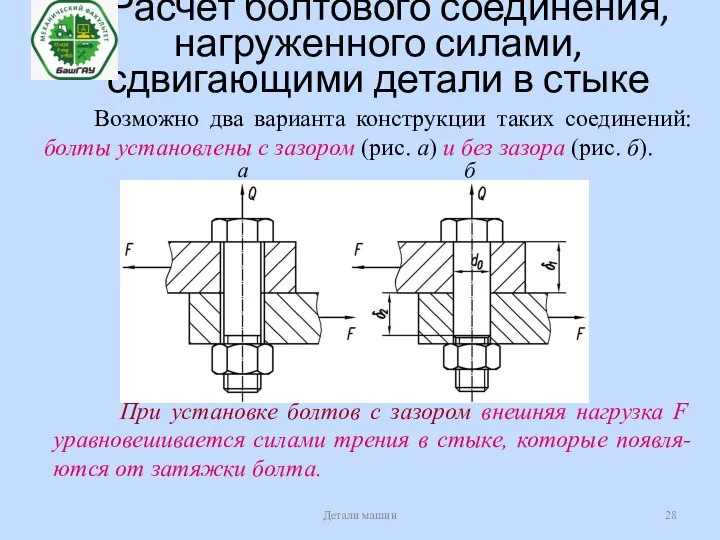
Расчет болтового соединения,
нагруженного силами,
сдвигающими детали в стыке
Детали машин
Возможно два варианта конструкции таких соединений: болты установлены с зазором (рис. а) и без зазора (рис. б).
а б
При установке болтов с зазором внешняя нагрузка F уравновешивается силами трения в стыке, которые появля-ются от затяжки болта.

Расчет болтового соединения, нагруженного силами,
сдвигающими детали в стыке
Детали машин
Условие отсутствия сдвига деталей представим в виде
F ≤ iFтр = iFзатf,
где i − число плоскостей стыка (при соединении двух деталей имеем одну плоскость стыка − i = 1); f − коэффициент трения в стыке (f = 0,15…0,2 для сухих чугунных и стальных поверх-ностей).
Отсюда определяют усилие затяжки
Fзат =KF/(if),
где K − коэффициент запаса (K = 1,3…1,5 при статической нагрузке, K = 1,8…2 при переменной нагрузке).
При установке болта без зазора отверстие калибруют разверт-кой, а диаметр стержня болта выполняют с допуском, обеспечи-вающим посадку с натягом. Болт рассчитывают на срез, а кон-тактные поверхности болта с деталями стыка - на смятие.

Расчет болтового соединения, нагруженного силами, сдвигающими детали в стыке
Условие прочности по напряжениям среза
τ = 4F/(πd02i) ≤ [τ],
где [τ] − допускаемое касательное напряжение для стержня болта, [τ] = (0.2…0.3)σт.
При расчете напряжений смятия принимают допущение об их равномерном распределении по контактной поверхности. Условия прочности по напряжениям смятия в этом случае имеют вид:
σсм = F/(dδmin) ≤ [σсм].
Допускаемое напряжение [σсм] = 0,8σТ, определяют по более слабому материалу. Толщину δmin берут меньшую
Детали машин

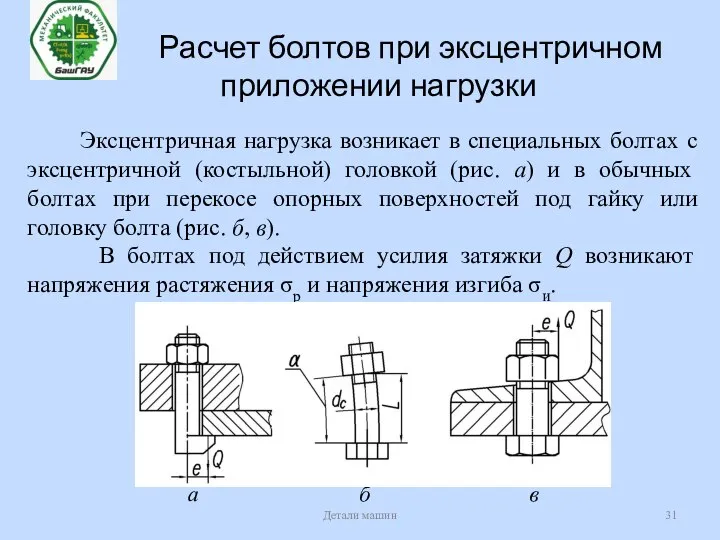
Расчет болтов при эксцентричном приложении нагрузки
Детали машин
Эксцентричная нагрузка возникает в специальных болтах с эксцентричной (костыльной) головкой (рис. а) и в обычных болтах при перекосе опорных поверхностей под гайку или головку болта (рис. б, в).
В болтах под действием усилия затяжки Q возникают напряжения растяжения σр и напряжения изгиба σи.
а б в

Расчет болтов при эксцентричном приложении нагрузки
Детали машин
Наибольшее суммарное напряжение
σЕ = 1.3 σр + σи,
где e - эксцентриситет.
После подстановки σр и σи и преобразований получим
σЕ = σр (1.3 + 8e/d1).
Принимая для схемы по рис. в, что e = d1, получим σЕ = 9,3σр.
Для исключения таких неблагоприятных схем нагружения опорные поверхности деталей, взаимодействующие с гайками или головками болтов, оформляют в виде зенковок (рис. 2, а) или бобышек (рис. 2, б).

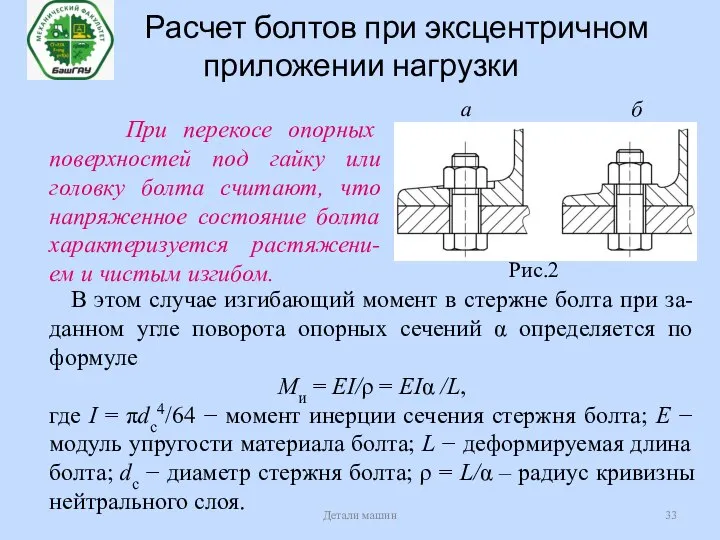
Расчет болтов при эксцентричном приложении нагрузки
Детали машин
При перекосе опорных поверхностей под гайку или головку болта считают, что напряженное состояние болта характеризуется растяжени-ем и чистым изгибом.
а б
Рис.2
В этом случае изгибающий момент в стержне болта при за-данном угле поворота опорных сечений α определяется по формуле
Mи = EI/ρ = EIα /L,
где I = πdc4/64 − момент инерции сечения стержня болта; E − модуль упругости материала болта; L − деформируемая длина болта; dс − диаметр стержня болта; ρ = L/α – радиус кривизны нейтрального слоя.

Расчет группы болтов
Детали машин
Расчет сводится к определению расчетной нагрузки для наиболее нагруженного болта и оценке прочности этого болта по формулам предыдущего раздела. Различают три характерных случая расчета соединений, включающих группу болтов.
Случай 1. Равнодействующая нагрузка перпендикулярна плос-кости стыка и проходит через его центр тяжести
Все болты такого соединения нагружены одинаково. Внешняя нагрузка, приходящаяся на один болт,
F = R/z,
где R − равнодействующая, нагружающая соединение;
z − число болтов соединения.
Далее используются формулы для расчета затянутого болто-вого соединения, нагруженного внешней осевой силой.

Расчет группы болтов
Детали машин
Случай 2. Равнодействующая нагрузка лежит в плоскости стыка
Примером служит крепление кронштейна к основанию (см. рис.). При расчете соединения равнодействующую, рас-положенную на расстоянии L от центра тяжести стыка, заме-няем силой, приложенной в центре тя-
жести стыка, и моментом T = RL.
Момент и сила стремятся повер-нуть и сдвинуть кронштейн. Нагрузка от силы R распределена по болтам рав-номерно FR =R/z. Нагрузки от момента FТi распределяются по болтам пропор-ционально расстоянию ri от болтов до центра тяжести стыка и направлены перпендикулярно радиусам ri.

Расчет группы болтов
Детали машин
FT1/r1= FT2/r2=…= FTn/rn = q,
где q − удельная нагрузка, приходящаяся на 1 мм расстояния от центра тяжести стыка.
Для определения q используют условие равновесия кронштей-на под действием приложенных моментов
T = r1FТ1 + r2FТ2 +…+ rnFТn.
После подстановки сюда значений нагрузок FТi = qri и преоб-разований получают
Далее определяют нагрузки FТi = qri. Для каждого болта геометрически находят равнодействующую сил FТi и FR. Из полученных равнодействующих для дальнейшего расчета выбирают максимальную величину Fmax.

Расчет группы болтов
Детали машин
Случай 3. Нагрузка соединения раскрывает стык
Последовательность решения для этого случая нагружения рассмотрим на примере крепления кронштейна, представленного на рис. Примем, что болты установлены с зазором. Рас-кладываем равнодействующую, при-ложенную к кронштейну, на верти-кальную R1 и горизонтальную R2 составляющие. Переносим эти сос-тавляющие в центр тяжести стыка с добавлением момента
M = R2L2 − R1L1.

Расчет группы болтов
Детали машин
Сила R1 и момент M раскрывают стык, а сила R2 сдвигает кронштейн в плоскости стыка. Для исключения раскрытия стыка и смещения кронштейна необходимо затянуть болты с усилием затяжки Q. Следовательно, при определении усилия затяжки выполняют два расчета: по условию нераскрытия стыка и по условию отсутствия смещения деталей в стыке. Из двух полученных усилий затяжки выбирают наибольшее.
Расчет по условию нераскрытия стыка
Напряжения смятия в стыке от усилия затяжки болтов
σзат = Qz/Aст,
где z − число болтов; Aст − площадь стыка.
Сила R1 растягивает болты и уменьшает напряжения в стыке на величину σR:
σR = R1(1 − χ)/Aст.

Расчет группы болтов
Детали машин
Экспериментально установлено, что напряжения в стыке под действием момента M изменяются в соответствии с эпюрой, аналогичной эпюре напряжений при изгибе.
Примем, что поворот кронштейна при действии момента M осуществляется относительно центра тяжести стыка, тогда
σM =M (1 − χ)/Wст,
где Wст − момент сопротивления изгибу поверхности стыка.
Минимальное и максимальное напряжения в стыке:
σmin = σзат − σR − σM,
σmax = σзат − σR + σM,
Условие нераскрытия стыка σmin > 0 запишем в виде
σзат = K (σR + σM),
где K = 1,3…2 - коэффициент запаса по нераскрытию стыка.
Усилие затяжки на основании формулы: Q = σзатAст/z.

Расчет группы болтов
Детали машин
Расчет по условию отсутствия смещения деталей в стыке
Если не предусмотрены разгрузочные устройства, то сила R2 уравновешивается силами трения в стыке. Смещение деталей не происходит при выполнении условия
Fтр = KтрR2,
где Fтр = f (Qz − R1); Kтр = 1,3…2 − коэффициент запаса по от-сутствию сдвига; f − коэффициент трения в стыке (ориентиро-вочно можно принять f = 0,15…0,2 − сталь по стали).
Отсюда усилие затяжки
Q = ( KтрR2/f + R1)/z.
Расчет на прочность болтов соединения
Внешняя нагрузка на наиболее нагруженный болт соеди-нения складывается из двух составляющих:
F = FR+FM,