Содержание
- 2. Темя для СРС: Распределение молекул по скоростям (закон Максвелла) Закон распределения Больцмана Число столкновений и средняя
- 3. 1.1 Предмет молекулярной физики Термодинамика и молекулярная физика изучает строение и физические свойства тел, а также
- 4. Статистический и термодинамический методы исследования Процессы, изучаемые молекулярной физикой, являются результатом совокупного действия огромного числа молекул.
- 5. 1.1.1 Новая физическая величина. Закон Авогадро Количество вещества определяется числом атомов или молекул содержащихся в данном
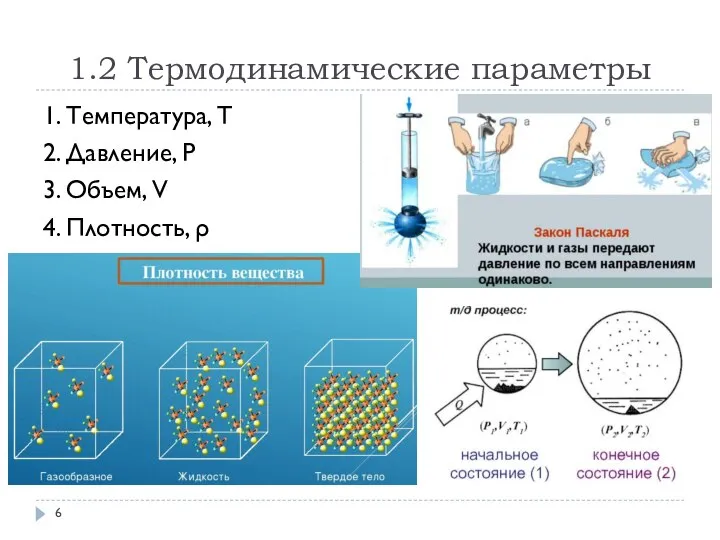
- 6. 1.2 Термодинамические параметры 1. Температура, T 2. Давление, P 3. Объем, V 4. Плотность, ρ
- 7. 1.2 Температура Температура – величина, характеризующая степень нагретости тела Характеризует состояние термодинамического равновесия системы тел Температура
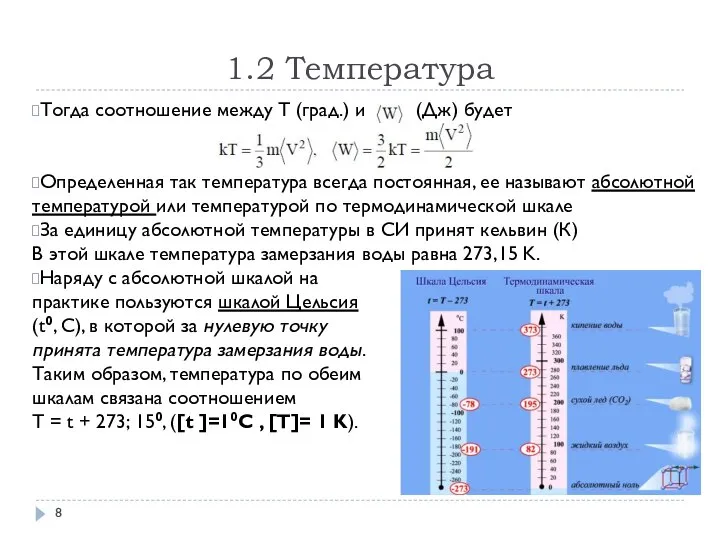
- 8. 1.2 Температура Тогда соотношение между T (град.) и (Дж) будет Определенная так температура всегда постоянная, ее
- 9. 1.3 Давление. Плотность Давление P - отношение силы, действующей на стенку перпендикулярно к её поверхности к
- 10. 1.4 Идеальный газ Наиболее простыми свойствами, которые можно описать уравнением состояния, обладает газ, находящийся в таких
- 11. 1.4 Скорости молекул газа. Средняя скорость молекул в газе обычно характеризуется среднеквадратичной или тепловой скоростью Т.к.
- 12. 1.5 Уравнение Менделеева – Клайперона для идеального газа (1) R- универсальная газовая постоянная, причём R=8,314 Для
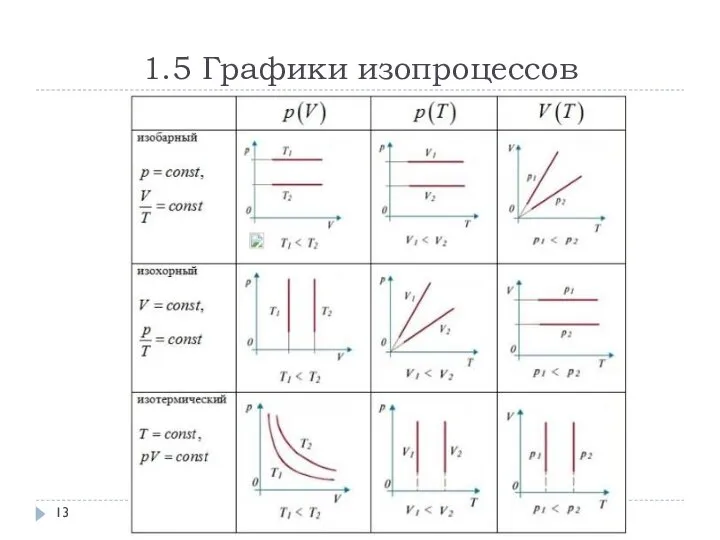
- 13. 1.5 Графики изопроцессов
- 14. 1.6 Закон Дальтона Пусть в сосуде с объёмом V находится в термическом равновесии смеси различных химически
- 15. 1.6 Закон Дальтона
- 16. 2. Основы термодинамики. Внутренняя энергия идеального газа Энергия тела складывается из энергии его движения как целого
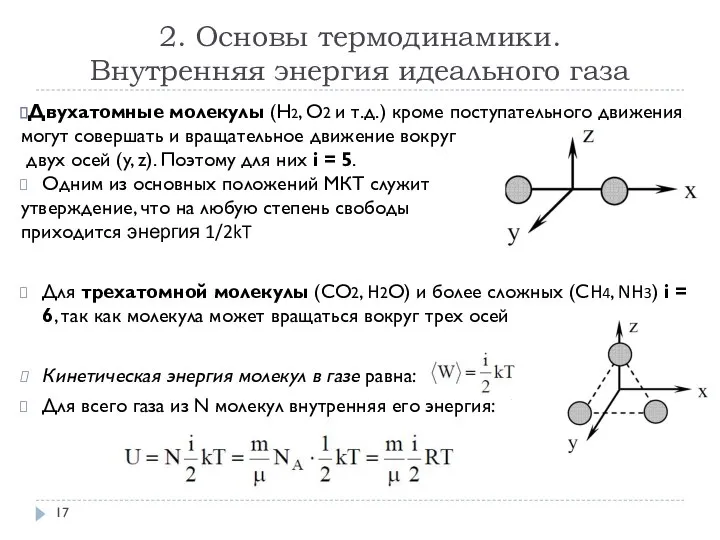
- 17. 2. Основы термодинамики. Внутренняя энергия идеального газа Двухатомные молекулы (Н2, О2 и т.д.) кроме поступательного движения
- 18. 2.1 Первое начало термодинамики Внутренняя энергия тела может изменяться либо за счет работы, которую над ним
- 19. 2.2 Работа при расширении газа При перемещении поршня на dx внешняя сила F совершает работу ,
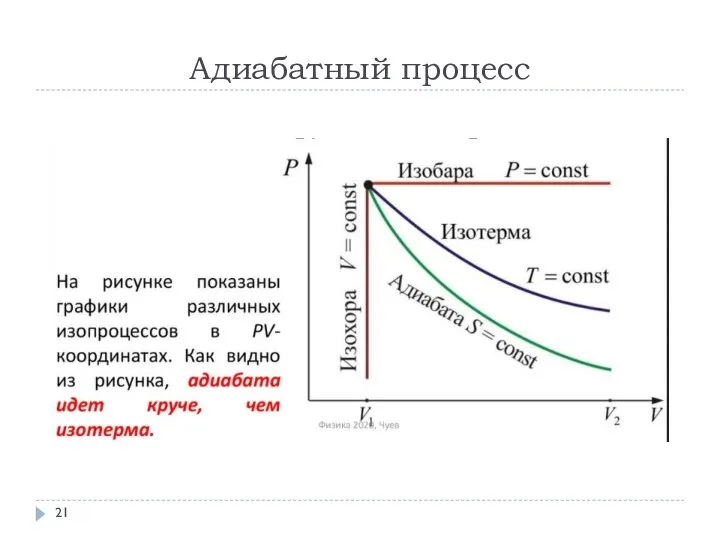
- 20. Адиабатный процесс Процесс, происходящий без теплообмена с внешней средой(обычно отсутствие теплообмена связано с быстротой процесса: теплообмен
- 21. Адиабатный процесс
- 22. Применение первого закона термодинамики к изопроцессам
- 24. Скачать презентацию
















 Переменный электрический ток
Переменный электрический ток Изучение явления электромагнитной индукции
Изучение явления электромагнитной индукции Фотоколориметрия
Фотоколориметрия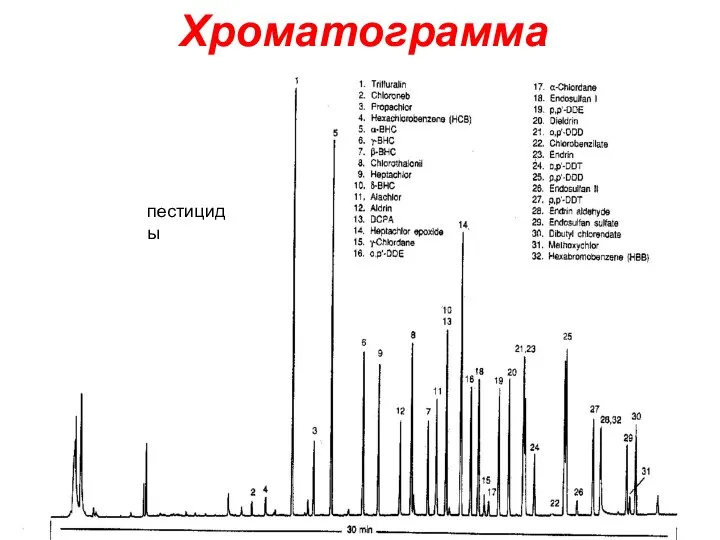 Хроматограмма пестициды
Хроматограмма пестициды Сообщающиеся сосуды
Сообщающиеся сосуды Свойства материалов
Свойства материалов Сила тяжіння. Вага тіла. Невагомість
Сила тяжіння. Вага тіла. Невагомість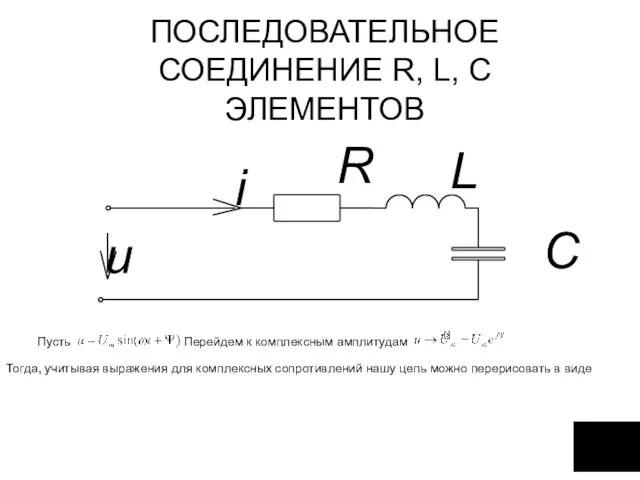 Последовательное соединение R, L, C элементов
Последовательное соединение R, L, C элементов Измерение скоростей продольных волн в образцах методом прямого просвечивания
Измерение скоростей продольных волн в образцах методом прямого просвечивания Однородное и неоднородное магнитное поле. Направление тока и направление линий его магнитного поля
Однородное и неоднородное магнитное поле. Направление тока и направление линий его магнитного поля Понятие индукции
Понятие индукции Город Инерция
Город Инерция Количество теплоты. Тест. 8 класс
Количество теплоты. Тест. 8 класс Маъруза №15. Умумий маълумотлар
Маъруза №15. Умумий маълумотлар Движение под действием закона всемирного тяготения
Движение под действием закона всемирного тяготения Презентация на тему Плавление и отвердевание кристаллических тел
Презентация на тему Плавление и отвердевание кристаллических тел  Сопротивляемость человеческого тела в разных условиях
Сопротивляемость человеческого тела в разных условиях Решение задач. Электромагнитная индукция
Решение задач. Электромагнитная индукция Работа, мощность, энергия. Обобщающий урок
Работа, мощность, энергия. Обобщающий урок Интерференция и дифракция механических волн
Интерференция и дифракция механических волн Напряженность электростатического поля
Напряженность электростатического поля Неньютоновская жидкость
Неньютоновская жидкость Типы шлифовальных станков
Типы шлифовальных станков Презентация урока физики в 8 классе «Параллельное соединение проводников ». Автор: Глазунова Лидия Ивановна, учитель физики МБО
Презентация урока физики в 8 классе «Параллельное соединение проводников ». Автор: Глазунова Лидия Ивановна, учитель физики МБО Действие электрического тока на человека
Действие электрического тока на человека Физика и познание мира
Физика и познание мира Импульс тела. Закон сохранения импульса
Импульс тела. Закон сохранения импульса Работа силы упругости
Работа силы упругости