Вывод формулы Резерфорда для вероятности обратного рассеяния альфа-частиц. АФ1.A

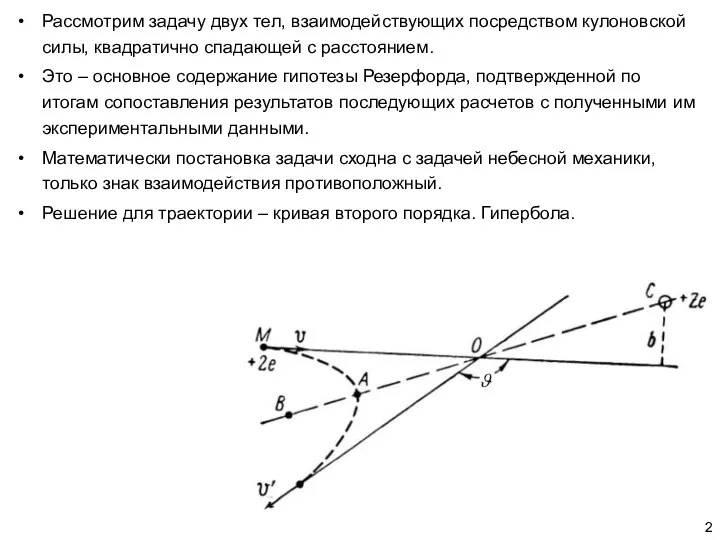
Рассмотрим задачу двух тел, взаимодействующих посредством кулоновской силы, квадратично спадающей с расстоянием.
Это – основное содержание гипотезы Резерфорда, подтвержденной по итогам сопоставления результатов последующих расчетов с полученными им экспериментальными данными.
Математически постановка задачи сходна с задачей небесной механики, только знак взаимодействия противоположный.
Решение для траектории – кривая второго порядка. Гипербола.

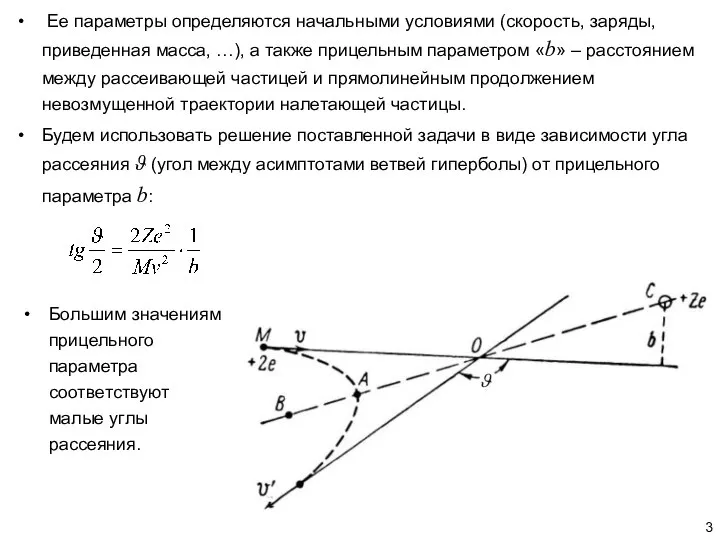
Ее параметры определяются начальными условиями (скорость, заряды, приведенная масса, …), а также прицельным параметром «b» – расстоянием между рассеивающей частицей и прямолинейным продолжением невозмущенной траектории налетающей частицы.
Будем использовать решение поставленной задачи в виде зависимости угла рассеяния ϑ (угол между асимптотами ветвей гиперболы) от прицельного параметра b:
Большим значениям прицельного параметра соответствуют малые углы рассеяния.

Вычислим вероятность того, что прицельный параметр пробной α-частицы, случайно «запущенной» в пределах участка мишени площадью S, по отношению к одной конкретной рассеивающей частице будет принадлежать интервалу [b; b+db].
Из рисунка, эта вероятность равна отношению площадей:
Умножив полученное значение на число рассеивающих частиц в рассматриваемой части мишени, получим вероятность dw того, что прицельный параметр пробной частицы окажется в интервале [b; b+db] по
отношению к одной из частиц мишени.
В этом случае, угол рассеяния будет близок к ϑ, удовлетворяющему условию

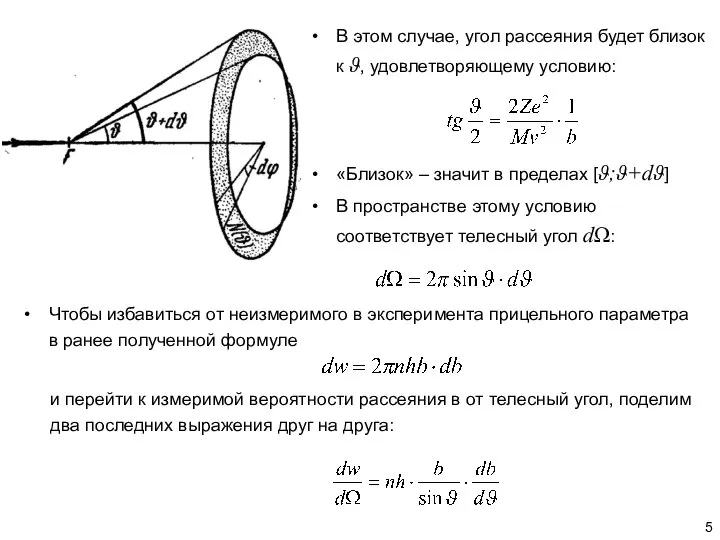
В этом случае, угол рассеяния будет близок к ϑ, удовлетворяющему условию:
«Близок» – значит в пределах [ϑ;ϑ+dϑ]
В пространстве этому условию соответствует телесный угол dΩ:
Чтобы избавиться от неизмеримого в эксперимента прицельного параметра в ранее полученной формуле
и перейти к измеримой вероятности рассеяния в от телесный угол, поделим два последних выражения друг на друга:

Сюда можно подставить зависимость b от угла рассеяния
?
Отсюда же вычислим и нужную нам производную (она отрицательна, но нам это неважно):
Подставив b и db/dϑ в верхнюю формулу, получим для вероятности рассеяния в телесный угол: