(внутренние усилия). Поэтому его называют методом сил.
Рассмотрим предыдущую балку и потребуем, чтобы ЗС и ее ОС были эквивалентными. Для этого перемещение в направлении исключенной связи в ОС должно равняться нулю: Δ=0.
Т.к. сила X неизвестна, ΔX определить нельзя. Поэтому рассмотрим единичное состояние (ЕС) основной системы, где действует только единичная сила P=1.
По принципу суперпозиции, перемещение Δ равно сумме перемещения ΔX от реакции X и перемещения ΔP от заданной силы P :
Δ=ΔX+ΔP=0.
Перемещение δ от единичной силы называется податливостью.
В линейно-упругой системе выполняется условие ΔX =δ X.
Тогда получаем каноническое уравнение метода сил:
δ X+ΔP=0.
Из него определяется неизвестная сила: X= – ΔP /δ .






 Качественный и количественный характеристики измеряемых величин
Качественный и количественный характеристики измеряемых величин Плавание судов и воздухоплавание
Плавание судов и воздухоплавание Механические колебания и волны
Механические колебания и волны Физика для одноклассников. 10 класс
Физика для одноклассников. 10 класс Первый закон термодинамики. Необратимость процессов в природе
Первый закон термодинамики. Необратимость процессов в природе На чем мы плаваем?
На чем мы плаваем?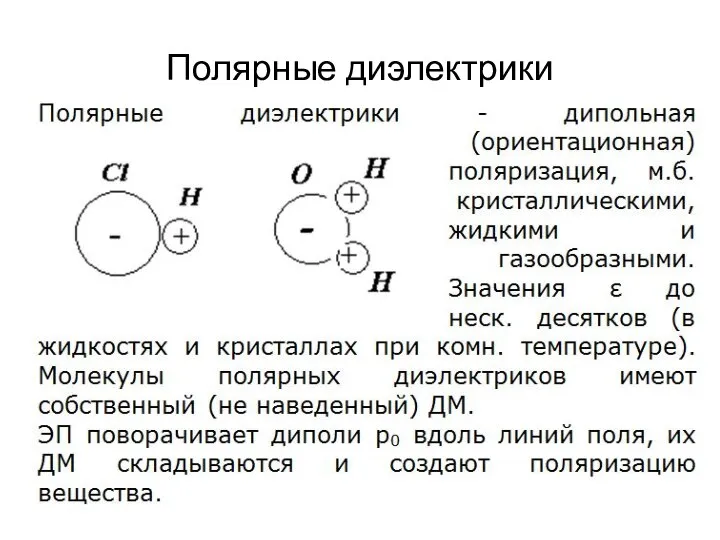 Полярные диэлектрики
Полярные диэлектрики Система охлаждения
Система охлаждения Свободные и вынужденные электромагнитные колебания
Свободные и вынужденные электромагнитные колебания Исследовательская работа по физике
Исследовательская работа по физике Демонстрационный вариант контрольных измерительных материалов единого государственного экзамена 2014 года по физике
Демонстрационный вариант контрольных измерительных материалов единого государственного экзамена 2014 года по физике Предмет и задачи динамики. Аксиомы динамики
Предмет и задачи динамики. Аксиомы динамики Виды движения по форме траектории
Виды движения по форме траектории муниципальное казенное общеобразовательное учреждение «Средняя общеобразовательная школа №4 п. Тавричанка Надеждинского района
муниципальное казенное общеобразовательное учреждение «Средняя общеобразовательная школа №4 п. Тавричанка Надеждинского района Статика. Условие равновесия
Статика. Условие равновесия Закон Архимеда. Лабораторная работа
Закон Архимеда. Лабораторная работа Поиск материалов с заданными свойствами. Практическая работа
Поиск материалов с заданными свойствами. Практическая работа Помощь в изучении тем по физике (на примере силы Архимеда)
Помощь в изучении тем по физике (на примере силы Архимеда) Трение - полезное или вредное явление?
Трение - полезное или вредное явление? Презентация на тему Изопроцессы в газах
Презентация на тему Изопроцессы в газах  Строение вещества, атома
Строение вещества, атома Теоретическая механика. Модуль 1. Раздел 3 – динамика точки
Теоретическая механика. Модуль 1. Раздел 3 – динамика точки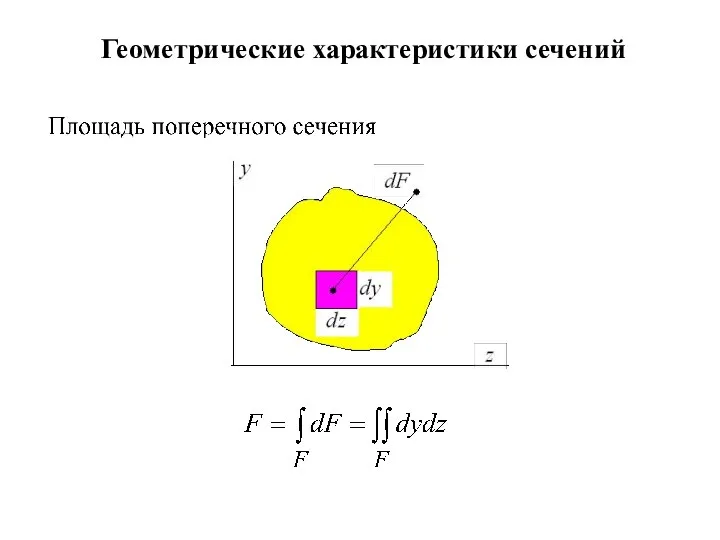 Prezentatsia_7
Prezentatsia_7 Радиоуглеродный анализ. Естественные науки в помощь гуманитарным
Радиоуглеродный анализ. Естественные науки в помощь гуманитарным Получение радиоактивных изотопов и их применение
Получение радиоактивных изотопов и их применение Механическая работа
Механическая работа Теоремы статики
Теоремы статики Обобщающий урок по теме « Электростатика» Цели урока: образовательные: Формирование и систематизация первоначальных пре
Обобщающий урок по теме « Электростатика» Цели урока: образовательные: Формирование и систематизация первоначальных пре