Слайд 2План лекции
Закон Кулона. Напряжённость электрического поля.
Электростатический потенциал.
Поле точечного диполя
Диполь в поле
Теорема

Гаусса. Электрические поля в простейших случаях.
Слайд 4Определения
Электромагнитное взаимодействие – фундаментальное взаимодействие, которое осуществляется на расстоянии посредством электромагнитного поля.
Электромагнитное

поле создаётся электрическими зарядами и действует на заряды
Заряд – мера взаимодействия заряженного тела с полем. Заряды бывают положительные и отрицательные
Носителями заряда являются элементарные частицы – протон (положительный заряд) и электрон (отрицательный заряд).
Элементарный заряд – заряд элементарных частиц
e = 4,803 . 10-10 ед. СГСЭ = 1,601 . 10-19 Кл (СИ)
Суммарный электрический заряд замкнутой системы сохраняется.
Заряд тела, системы тел – релятивистский инвариант: при переходе от одной инерциальной системы отсчёта к другой заряд не изменяется.
Слайд 5Электростатика
Электростатика занимается изучением полей неподвижных зарядов.
Неподвижные заряды создают неизменное во времени

электростатическое поле.
Точечный заряд – это заряд, размером и формой которого в рассматриваемых условиях можно пренебречь
Пробный заряд – небольшой по величине точечный заряд, который не вызывает перераспределения электрических зарядов в окружающих телах.
Слайд 6Закон Кулона (1875 г)
Сила взаимодействия двух точечных зарядов в вакууме направлена вдоль

прямой, соединяющей эти заряды, пропорциональна их величинам q и Q и обратно пропорциональна квадрату расстояния между ними r. Одноимённые заряды отталкиваются; заряды разных знаков притягиваются.
F = Qq/r2
Закон Кулона в векторной форме:
F = Qqr/r3
Слайд 7Напряжённость электрического поля
Напряжённостью электрического поля называется сила, действующий на единичный заряд:
E =

F/q, F = qE
Поле точечного заряда Q:
E = Qr/r3
Принцип суперпозиции:
напряжённость электрического поля E нескольких неподвижных точечных зарядов равна векторной сумме напряжённостей полей, которое создавал бы каждый из этих зарядов в отсутствие остальных:
E = ΣEi
Слайд 8Принцип суперпозиции для электростатических полей
Электрическое взаимодействие между двумя зарядами не зависит от
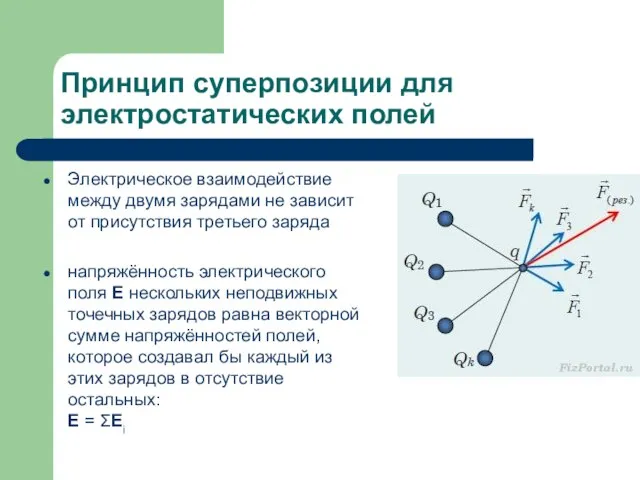
присутствия третьего заряда
напряжённость электрического поля E нескольких неподвижных точечных зарядов равна векторной сумме напряжённостей полей, которое создавал бы каждый из этих зарядов в отсутствие остальных:
E = ΣEi
Слайд 9Потенциал электростатического поля
Электростатическое поле потенциально, как всякое стационарное центральное поле ⇨ работа

поля не зависит от траектории и равна убыли потенциальной энергии взаимодействия:
dU = -(qQ/r2)dr ⇨
U = qQ/r; U(∞) = 0
Потенциал электрического поля – это потенциальная энергия единичного заряда. Потенциал точечного заряда φ(r) = Q/r
Принцип суперпозиции для потенциала: потенциал поля системы зарядов равен сумме потенциалов полей отдельных зарядов
φ(r) = φ1(r) + φ2(r) + …
Энергия заряда в поле U = qφ
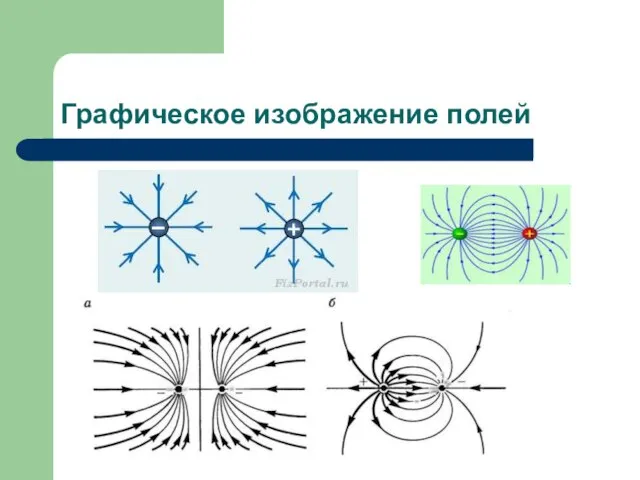
Слайд 11Как устроены силовые линии.
Направление касательной в каждой точке силовой линии совпадает с

вектором E
Силовые линии не пересекаются в пространстве, не содержащих заряды
Линии электростатического поля не могут быть замкнутыми – это противоречило бы закону сохранения энергии
один конец силовой линии – всегда заряд; другой конец - либо заряд противоположного знака, либо бесконечность.
Слайд 12Поле на оси равномерно заряженного диска
Поле на оси равномерно заряженного диска с

поверхностной плотностью σ = Q/πR2 на расстоянии z от поверхности диска
dE = dEz = σcosθρdρdφ/r2 = σdS┴/r2 = σdΩ ⇨
E = σΩ
R >> z (заряженная плоскость) Ω = 2π ⇨ E = 2πσ
Z >> R (точечный заряд) Ω = S/z2 ⇨ E = σS/z2 = Q/z2
В общем случае: dΩ = sinθdθdφ ⇨
Ω = 2π(1 - cos θ) = 2π(1 – z/(z2 + R2)1/2)
E = σΩ = 2πσ(1 – z/(z2 + R2)1/2)
Слайд 13Поле короткой заряженной нити
Заряд равномерно распределён по отрезку прямой нити с линейной
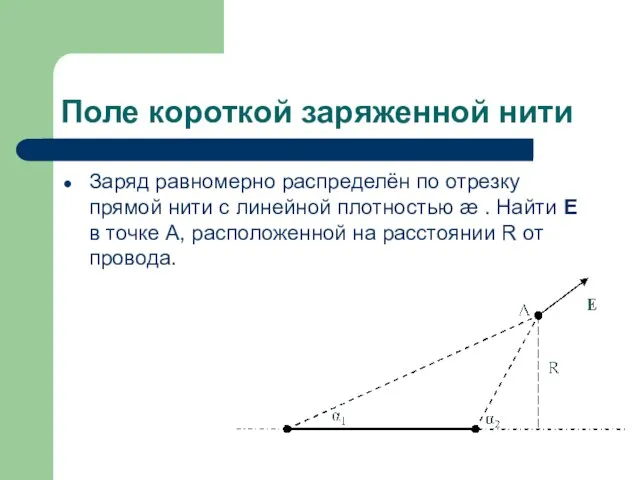
плотностью ӕ . Найти E в точке А, расположенной на расстоянии R от провода.
Слайд 14Поле короткого провода
Ey =∫dEy = ∫ӕdlsinα/r2 = ∫ӕdφ/r = ∫ӕcosφdφ/R =
ӕ/R

(sinφ1 – sinφ2) = ӕ(cosα1 – cosα2)/R
Ex =∫dEx = ∫ӕdlcosα/r2 = ∫ӕsinφdφ/R=
ӕ/R (cosφ2 – cosφ1) = ӕ(sinα2 – sinα1)/R
Бесконечный провод: α1 = 0; α2 = 1800 ⇨ E = Ey = 2ӕ/R; Ex = 0
Полубесконечный провод: α1 = 0; α2 = 900 ⇨ Ex = Ey = ӕ/R
Слайд 15Электрический диполь
Простейший электрический диполь – эта система равных по величине, но противоположных

по знаку двух точечных зарядов –q и +q, сдвинутых друг относительно друга на рассстояние ℓ.
Плечо диполя – это вектор ℓ, проведённый от отрицательного к положительному заряду
Вектор p = qℓ называется дипольным моментом
Диполь называется точечным, если ℓ значительно меньше расстояния r до точки наблюдения: ℓ << r
Диполь называется жёстким, если расстояние между зарядами ℓ неизменно.
Диполь называется упругим, если расстояние между зарядами ℓ меняется под действием внешних сил.
Слайд 16Диполь во внешнем поле
В однородном электрическом поле на диполь действует момент сил

M = [ℓ F] = q[ℓ E] = [p E], M = - pE sinθ – в электрическом поле диполь ориентируется вдоль вектора напряжённости E
Энергия точечного диполя: W = qφ(r +ℓ) + qφ(r) =
q (gradφ,ℓ) = - (p,E)
В неоднородном поле на диполь действует сила: Fx = qEx(r + ℓ) - qEx(r) = qℓx∂Ex/∂x + qℓy∂Ex/∂y + qℓz∂Ex/∂z = (p,gradEx) ⇨ F = px∂E/∂x + py∂E/∂y + pz∂E/∂z = (p,grad)E
Диполь выстраивается вдоль поля p ↑↑ E;
Ориентированный вдоль поля диполь втягивается в
область более сильного электрического поля.
Слайд 17Потенциал диполя: (pr)/r3
Поле диполя: E = 3 (pr)r/r5 – p/r3
Потенциал точечного

диполя:
φ = φ+ + φ- = q/r1 – q/r2 = q(r2 – r1)/r1r2 =
qℓcosθ/r2 = (pr)/r3
φ = (pr)/r3
Поле точечного диполя:
E = - grad φ = - grad (pr)/r3 = 3 (pr)r/r5 – p/r3
grad(1/r3) = -3r/r5;
grad(pr) = p
grad(r) = r/r
Слайд 18Оператор Гамильтона
(набла-оператор):
grad U =
Приращение
функции:
свойства:
grad(uv) = ugradv + vgradv

(“производная произведения”)
gradf(u) = (df/du) gradu (“производная сложной функции”)
Полезные формулы:
grad(p,r) = p
grad r = r/r – (поле единичных векторов)
grad 1/r = (-1/r2) (r/r) = - r/r3
Слайд 19Теорема Гаусса
(интегральная форма)
Поток вектора E сквозь замкнутую поверхность равен алгебраической сумме

зарядов внутри этой поверхности, умноженной на 4π:
Теорема Гаусса в дифференциальной форме:
divE = 4πρ
Слайд 20Теорема Гаусса
(дифференциальная форма)

Слайд 21Теорема Ирншоу – следствие теоремы Гаусса
Невозможно создать устойчивую систему только из покоящихся
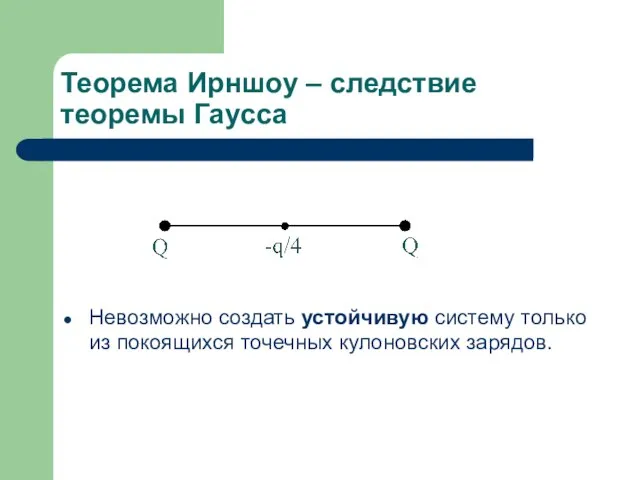
точечных кулоновских зарядов.
Слайд 22Применение теоремы Гаусса
Поле заряженной нити:
E.2πr.L = 4πq ⇨E = 2q/Lr = 2ӕ/r
Поле

заряженной плоскости:
Ф = Ф1 + Ф2 = EΔS + EΔS = 2EΔS = 4πΔq ⇨ E = 2πΔq/ΔS = 2πσ
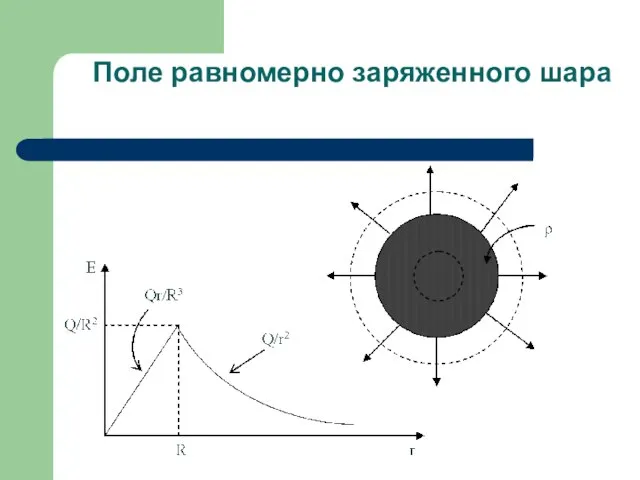
Поле равномерно заряженного шара:
Вне шара r > R: E 4πr2 = 4πQ ⇨ E = Q/r2
Внутри шара r < R: E 4πr2 = 4πq(r) = 4πQ(r/R)3 ⇨
E = Qr/R3 = 4/3 πρr
в векторном виде:
E = Qr/r3, r > R
E = Qr/R3 = 4/3 πρr, r < R
Слайд 23Поле равномерно заряженного шара
Слайд 24Связь потенциала с напряжённостью поля
Убыль потенциала равна работе поля:
φ(r) - φ(r +

dr) = Edr = Exdx + Eydy + Ezdz ⇨
Ex = -∂φ/∂x; Ey = -∂φ/∂y; Ez = -∂φ/∂z ⇨
E = - gradφ






















 Пневматика
Пневматика Презентация на тему Расчёт пути и времени движения
Презентация на тему Расчёт пути и времени движения  Движение тела в поле сил земного тяготения с учетом зависимости ускорения свободного падения от высоты
Движение тела в поле сил земного тяготения с учетом зависимости ускорения свободного падения от высоты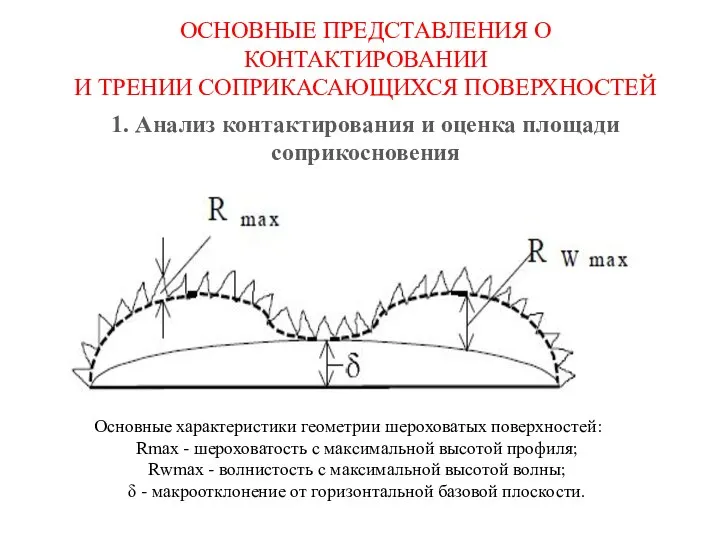 Основные представления о контактировании и трении соприкасающихся поверхностей
Основные представления о контактировании и трении соприкасающихся поверхностей Современные технологии обеспечения аэродинамических свойств легковых автомобилей
Современные технологии обеспечения аэродинамических свойств легковых автомобилей Механические передачи
Механические передачи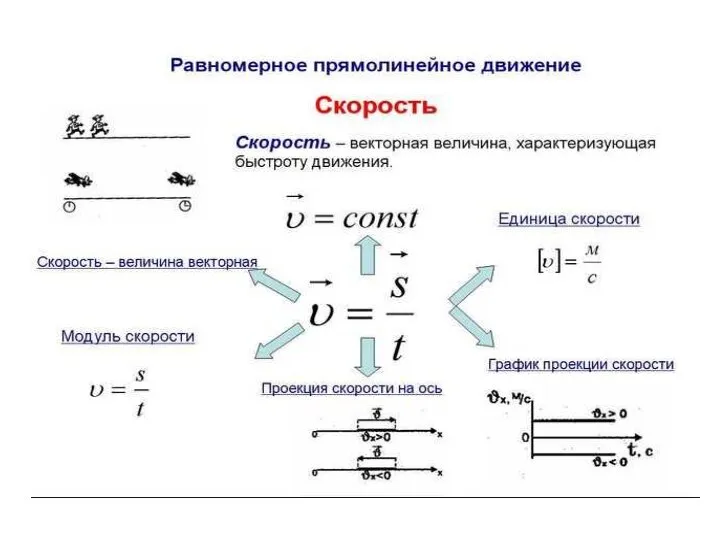 Равномерное прямолинейное движение
Равномерное прямолинейное движение Экспериментальное решение проблемы течи гидроблока МТА
Экспериментальное решение проблемы течи гидроблока МТА Колебания и волны. Лекция 3.1
Колебания и волны. Лекция 3.1 Виды, структура и утилизация батареек
Виды, структура и утилизация батареек Электрические явления
Электрические явления Квантовая механика
Квантовая механика Численная модель квазистационарного электромагнитного поля, индуцируемого в проводниках с дефектами
Численная модель квазистационарного электромагнитного поля, индуцируемого в проводниках с дефектами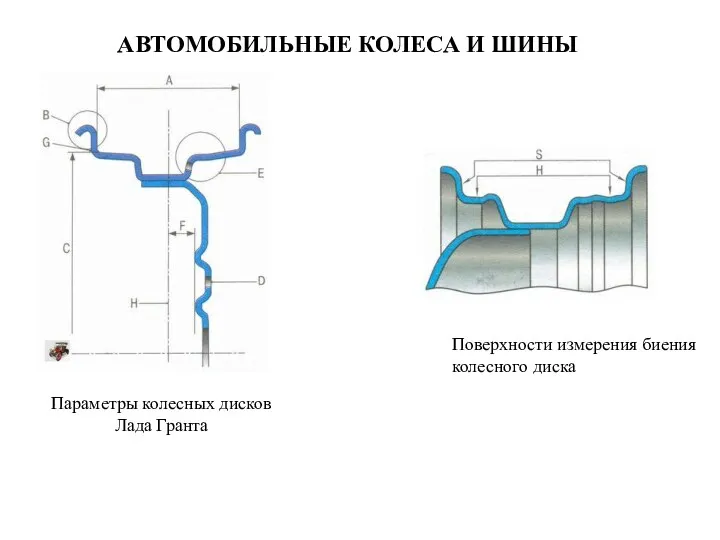 Автомобильные колеса и шины. Поверхности измерения биения колесного диска. Параметры колесных дисков Лада Гранта
Автомобильные колеса и шины. Поверхности измерения биения колесного диска. Параметры колесных дисков Лада Гранта Необычные виды транспорта. Поезд на магнитной подушке
Необычные виды транспорта. Поезд на магнитной подушке Задачи
Задачи Билет № 1, 4 (вопрос 3). Задача на формулу силы Лоренца
Билет № 1, 4 (вопрос 3). Задача на формулу силы Лоренца Электротехника и Электроника
Электротехника и Электроника Статические ИО тока. Лекции 10
Статические ИО тока. Лекции 10 Машины переменного тока
Машины переменного тока Контроль цилиндрических изделий наружными проходными ВТП с однородным магнитным полем
Контроль цилиндрических изделий наружными проходными ВТП с однородным магнитным полем Презентация на тему Применение конденсаторов
Презентация на тему Применение конденсаторов  Беседа Понятие об источниках тока
Беседа Понятие об источниках тока Муниципальное оздоровительное образовательное учреждение санаторного типа для детей, нуждающихся в длительном лечении – Томмот
Муниципальное оздоровительное образовательное учреждение санаторного типа для детей, нуждающихся в длительном лечении – Томмот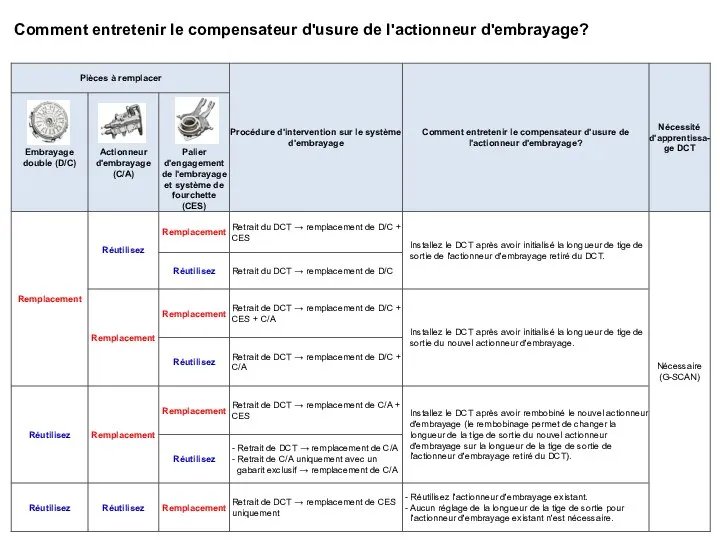 Comment entretenir le compensateur d'usure de l'actionneur d'embrayage
Comment entretenir le compensateur d'usure de l'actionneur d'embrayage Освещение. Виды освещения
Освещение. Виды освещения Ионизирующее излучение: природа, единицы измерения, биологические эффекты
Ионизирующее излучение: природа, единицы измерения, биологические эффекты Взаимодействие проводников с током
Взаимодействие проводников с током