Содержание
- 2. Литература Н. Ашкрофт, Н. Мермин, Физика твердого тела в 2х томах / пер. с англ А.С.
- 3. План лекции Введение Модели строения атома и квантовая теория Бора Волновые и карпускулярные свойства света и
- 4. План лекции Введение Модели строения атома и квантовая теория Бора Волновые и карпускулярные свойства света и
- 5. Введение Рождение квантовой механики как науки произошло в 1900 году благодаря немецкому физику-теоретику Максу Планку Макс
- 6. Введение Рождение квантовой механики как науки произошло в 1900 году благодаря немецкому физику-теоретику Максу Планку Макс
- 7. Ультрафиолетовая катастрофа До 1900 года – парадокс классической физики
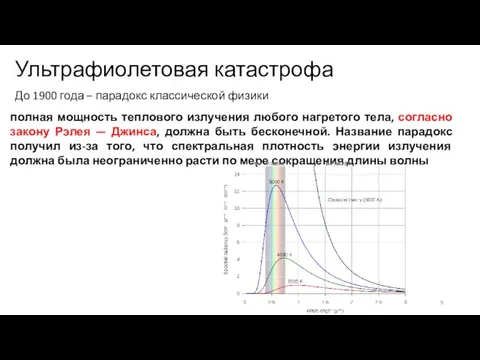
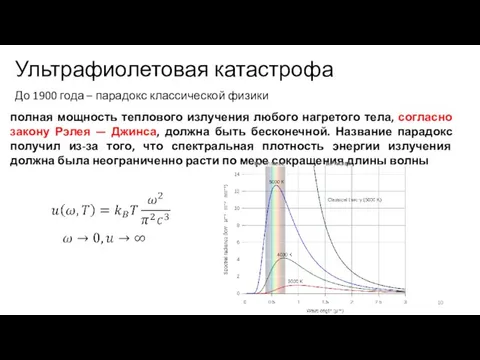
- 8. Ультрафиолетовая катастрофа До 1900 года – парадокс классической физики полная мощность теплового излучения любого нагретого тела,
- 9. Ультрафиолетовая катастрофа До 1900 года – парадокс классической физики полная мощность теплового излучения любого нагретого тела,
- 10. Ультрафиолетовая катастрофа До 1900 года – парадокс классической физики полная мощность теплового излучения любого нагретого тела,
- 11. Ультрафиолетовая катастрофа Планк сделал революционное предположение
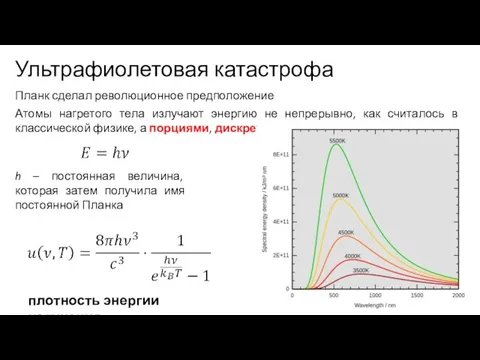
- 12. Ультрафиолетовая катастрофа Планк сделал революционное предположение Атомы нагретого тела излучают энергию не непрерывно, как считалось в
- 13. Ультрафиолетовая катастрофа Планк сделал революционное предположение Атомы нагретого тела излучают энергию не непрерывно, как считалось в
- 14. Ультрафиолетовая катастрофа Планк сделал революционное предположение Атомы нагретого тела излучают энергию не непрерывно, как считалось в
- 15. План лекции Введение Модели строения атома и квантовая теория Бора Волновые и карпускулярные свойства света и
- 16. Модели строения атома и квантовая теория Бора После открытия первой элементарной частицы-электрона в 1897 году были
- 17. Модели строения атома и квантовая теория Бора После открытия первой элементарной частицы-электрона в 1897 году были
- 18. Модели строения атома и квантовая теория Бора После открытия первой элементарной частицы-электрона в 1897 году были
- 19. Модели строения атома и квантовая теория Бора Модель Резерфорда Э. Резерфорд в 1911 году провел эксперимент
- 20. Модели строения атома и квантовая теория Бора Модель Резерфорда Э. Резерфорд в 1911 году провел эксперимент
- 21. Модели строения атома и квантовая теория Бора Модель Резерфорда Э. Резерфорд в 1911 году провел эксперимент
- 22. Модели строения атома и квантовая теория Бора В 1913 году Нильс Бор ввел в классическую физику
- 23. План лекции Введение Модели строения атома и квантовая теория Бора Волновые и корпускулярные свойства света и
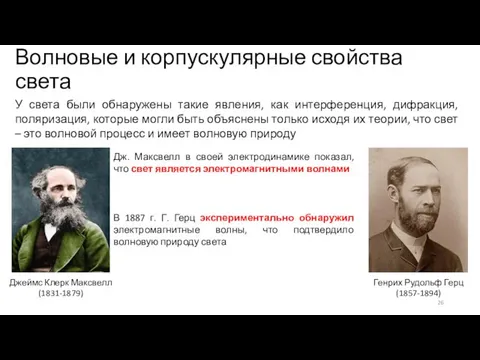
- 24. Волновые и корпускулярные свойства света У света были обнаружены такие явления, как интерференция, дифракция, поляризация, которые
- 25. Волновые и корпускулярные свойства света У света были обнаружены такие явления, как интерференция, дифракция, поляризация, которые
- 26. Волновые и корпускулярные свойства света У света были обнаружены такие явления, как интерференция, дифракция, поляризация, которые
- 27. Волновые и корпускулярные свойства света У света были обнаружены такие явления, как интерференция, дифракция, поляризация, которые
- 28. Фотоэффект Генрих Рудольф Герц (1857-1894) В 1887 г. Г. Герц экспериментально наблюдал и другое явление, которое
- 29. Фотоэффект Генрих Рудольф Герц (1857-1894) В 1887 г. Г. Герц экспериментально наблюдал и другое явление, которое
- 30. Фотоэффект Генрих Рудольф Герц (1857-1894) В 1887 г. Г. Герц экспериментально наблюдал и другое явление, которое
- 31. Фотоэффект Генрих Рудольф Герц (1857-1894) В 1887 г. Г. Герц экспериментально наблюдал и другое явление, которое
- 32. Фотоэффект Генрих Рудольф Герц (1857-1894) В 1887 г. Г. Герц экспериментально наблюдал и другое явление, которое
- 33. Волновые и корпускулярные свойства света Второй закон Столетова не мог быть объяснен с точки зрения волновой
- 34. Волновые и корпускулярные свойства света Второй закон Столетова не мог быть объяснен с точки зрения волновой
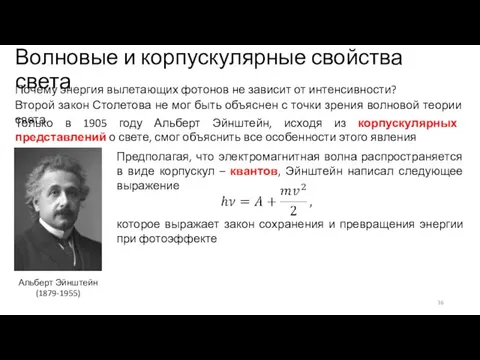
- 35. Волновые и корпускулярные свойства света Второй закон Столетова не мог быть объяснен с точки зрения волновой
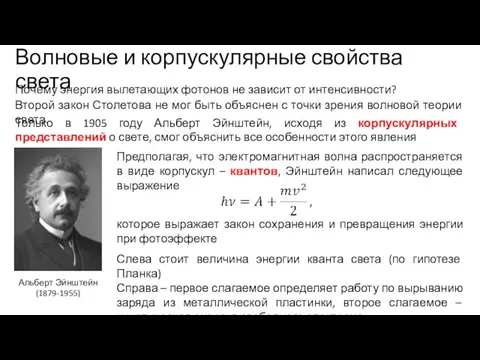
- 36. Волновые и корпускулярные свойства света Второй закон Столетова не мог быть объяснен с точки зрения волновой
- 37. Волновые и корпускулярные свойства света Второй закон Столетова не мог быть объяснен с точки зрения волновой
- 38. Волновые и корпускулярные свойства света Существуют явления (интерференция, дифракция, поляризация), в которых свет проявляет волновые свойства
- 39. Волновые и корпускулярные свойства света Существуют явления (интерференция, дифракция, поляризация), в которых свет проявляет волновые свойства
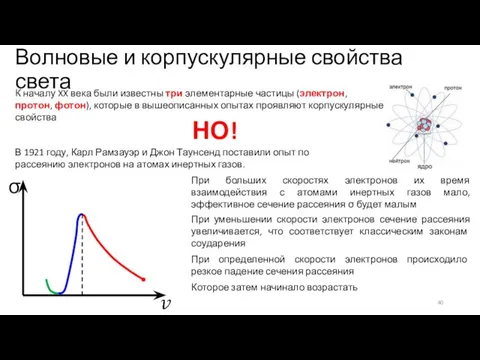
- 40. Волновые и корпускулярные свойства света К началу XX века были известны три элементарные частицы (электрон, протон,
- 41. Волновые и корпускулярные свойства света Для объяснения этого эффекта обратимся к Луи де Бройлю Луи де
- 42. Волновые и корпускулярные свойства света Для объяснения этого эффекта обратимся к Луи де Бройлю Луи де
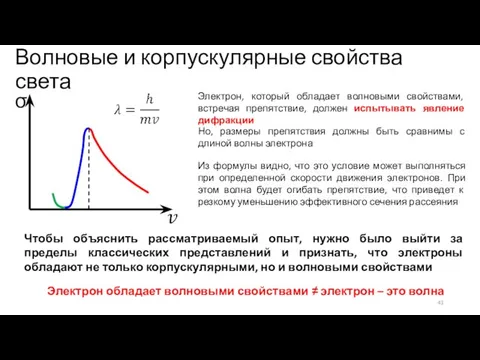
- 43. Волновые и корпускулярные свойства света σ Электрон, который обладает волновыми свойствами, встречая препятствие, должен испытывать явление
- 44. План лекции Введение Модели строения атома и квантовая теория Бора Волновые и корпускулярные свойства света и
- 45. Гипотеза де Бройля Де Бройль использовал формулы Эйнштейна для фотоэффекта, чтобы постулировать о волновых свойствах частиц
- 46. Гипотеза де Бройля Эти формулы связывают между собой корпускулярные и волновые характеристики свойств элементарных частиц Формулы
- 47. Гипотеза де Бройля Определим с какой скоростью перемещаются точки элементарной частицы, имеющие одну и ту же
- 48. Гипотеза де Бройля Применим формулы СТО и получим Таким образом, с фазовой скоростью волны де Бройля
- 49. Гипотеза де Бройля ИТОГ №1. Волновая функция де Бройля не имеет непосредственного физического смысла ИТОГ №2.
- 50. Гипотеза де Бройля Употреблять и сопоставлять микрочастице плоскую волну де Бройля нельзя из теории волновых процессов
- 51. Волновой пакет Построим волновой в виде суперпозиции волновых функций де Бройля Пусть частоты меняются в интервале
- 53. Скачать презентацию




































 Нерезьбовые соединения. Шпоночное соединение
Нерезьбовые соединения. Шпоночное соединение Физика. Трансформатор
Физика. Трансформатор Решение качественных и расчетных задач по физике
Решение качественных и расчетных задач по физике Физические величины. Измерение физических величин. Точность и погрешность измерений
Физические величины. Измерение физических величин. Точность и погрешность измерений Тепловые явления в природе
Тепловые явления в природе Уравнение Клапейрона
Уравнение Клапейрона Методы астрофизических исследований. Занятие 11
Методы астрофизических исследований. Занятие 11 Теория колебаний
Теория колебаний Презентация на тему Свойства газов
Презентация на тему Свойства газов  Простейшие движения твердого тела
Простейшие движения твердого тела Устойчивость САУ
Устойчивость САУ ПЗ 2 ДМ (1)
ПЗ 2 ДМ (1) Техосмотр
Техосмотр Источники света. Прямолинейное распространение света
Источники света. Прямолинейное распространение света Различие в молекулярном строении твёрдых тел, жидкостей и газов
Различие в молекулярном строении твёрдых тел, жидкостей и газов Основные понятия кинематики
Основные понятия кинематики Ферриты
Ферриты Жоғары рұқсат етілім литографиясы
Жоғары рұқсат етілім литографиясы Рабочие вещества холодильных машин и тепловых насосов
Рабочие вещества холодильных машин и тепловых насосов История числа «π» 6 класс - Презентация_
История числа «π» 6 класс - Презентация_ Оптимальное обнаружение сигнала с полностью известными параметрами
Оптимальное обнаружение сигнала с полностью известными параметрами Сообщающиеся сосуды
Сообщающиеся сосуды Теплопроводность через плоскую и цилиндрическую стенки при граничных условиях третьего рода (теплопередача)
Теплопроводность через плоскую и цилиндрическую стенки при граничных условиях третьего рода (теплопередача) Исследование эффекта Талбота с использованием компьютерных модулей
Исследование эффекта Талбота с использованием компьютерных модулей Автоматизированная информационная система Техосмотр
Автоматизированная информационная система Техосмотр Презентация на тему Термоядерная реакция
Презентация на тему Термоядерная реакция  « Физика в нашей жизни»
« Физика в нашей жизни» Экспертные советы по теоретической физике
Экспертные советы по теоретической физике