Содержание
- 2. В загальному випадку рівняння миттєвих синусоїдальних електричних величин мають вигляд: де e, i, u – миттєві
- 3. Зсувом фаз ϕ називається різниця початкових фаз двох будь-яких синусоїдальних величин однієї частоти. Періодом Т називається
- 4. Комплексний метод аналізу і розрахунку ланцюгів синусоїдального струму Комплексне число А виражається алгебраїчно у вигляді суми
- 5. Множення на j рівносильне повороту вектору на кут 90 градусів проти годинникової стрілки. Для комплексних чисел
- 6. Подання синусоїдальних електричних величин комплексними числами Комплексна амплітуда струму і напруги в показовій формі: , ,
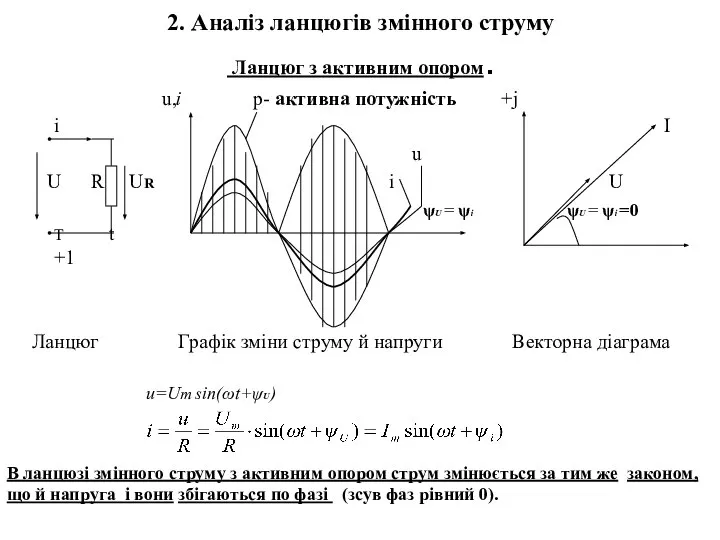
- 7. 2. Аналіз ланцюгів змінного струму Ланцюг з активним опором. u,i р- активна потужність +j і I
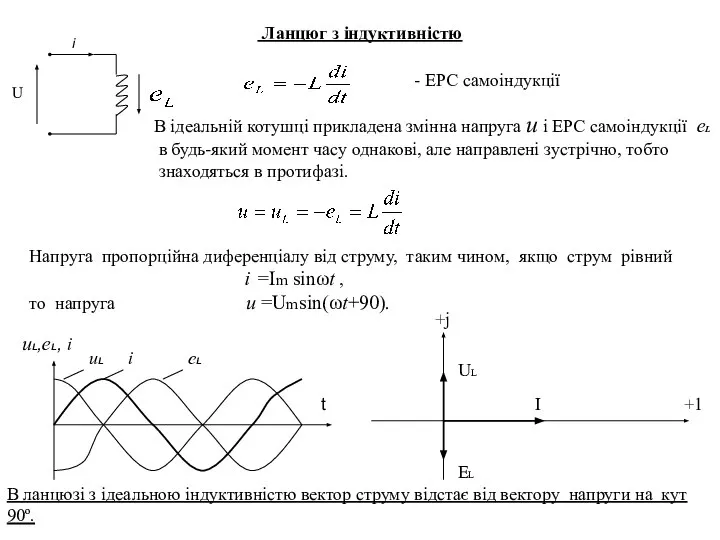
- 8. Ланцюг з індуктивністю i - ЕРС самоіндукції U В ідеальній котушці прикладена змінна напруга u і
- 9. Діюче значення змінного струму Отриманий вираз нагадує закон Ома для ланцюга постійного струму. У цій рівності
- 10. В ланцюзі з ідеальною ємністю вектор струму випереджає вектор напруги на кут 90º або чверть періоду.
- 11. 3. Послідовне з’єднання елементів R, L, C. Резонанс напруг Згідно 2 закону Кірхгофа при послідовному з’єднанні
- 12. Три варіанти співвідношень індуктивного і ємнісного опорів в колі: а) - активно-індуктивний характер кола; б) -
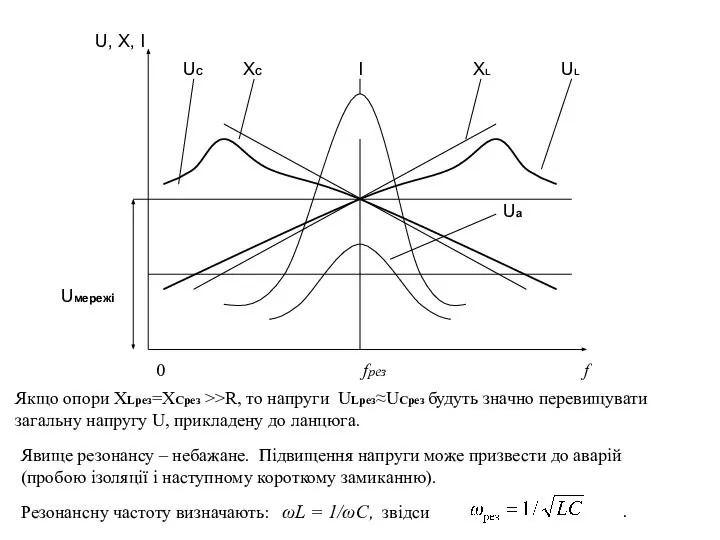
- 13. U, X, I UC XC I XL UL Uа Uмережі 0 fрез f Явище резонансу –
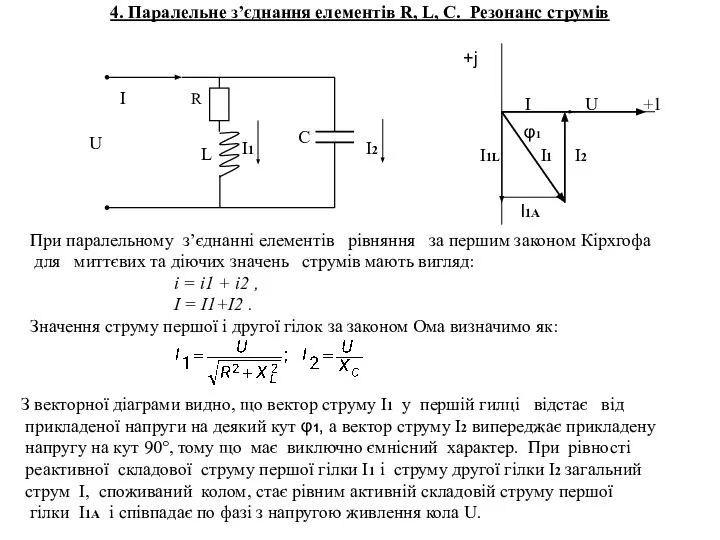
- 14. 4. Паралельне з’єднання елементів R, L, C. Резонанс струмів +j І U +1 При паралельному з’єднанні
- 15. Явище, при якому в колі з паралельно з'єднаними активно-індуктивним і ємнісним опорами реактивні провідності гілок рівні,
- 16. 5. Потужність кола синусоїдного струму Миттєва потужність кола синусоїдного струму визначається добутком миттєвого струму та миттєвої
- 18. Скачать презентацию











 Нанотехнологии – толчок в будущее человечества
Нанотехнологии – толчок в будущее человечества Термодинамика высокоэластичной деформации
Термодинамика высокоэластичной деформации Внутренняя энергия и способы ее изменения
Внутренняя энергия и способы ее изменения Электрический ток. Сила тока. Закон Ома. Сопротивление
Электрический ток. Сила тока. Закон Ома. Сопротивление Взаимодействие цвета и вещества
Взаимодействие цвета и вещества Презентация на тему Тепловое равновесие
Презентация на тему Тепловое равновесие  Саха теңдеуі
Саха теңдеуі Режимы работы гидромуфты. Передаточное отношение и КПД гидромуфты
Режимы работы гидромуфты. Передаточное отношение и КПД гидромуфты Расчёт пути и времени движения
Расчёт пути и времени движения Анализ видов и кинематических параметров движений
Анализ видов и кинематических параметров движений Квантовые свойства электромагнитного излучения
Квантовые свойства электромагнитного излучения Магнитное поле
Магнитное поле Матрицы и действия над ними
Матрицы и действия над ними Источники света. Распространение света
Источники света. Распространение света Сила тока. Единицы силы тока. Амперметр. Измерение силы тока. МБОУ СОШ № 91 Г. Красноярск Тычкова Н.А.
Сила тока. Единицы силы тока. Амперметр. Измерение силы тока. МБОУ СОШ № 91 Г. Красноярск Тычкова Н.А. Специальная теория относительности
Специальная теория относительности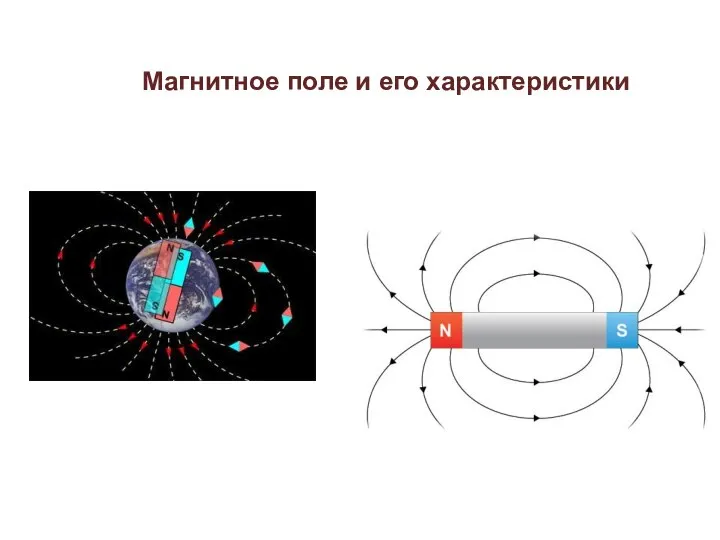 магнитное поле (1)
магнитное поле (1) Tok energie
Tok energie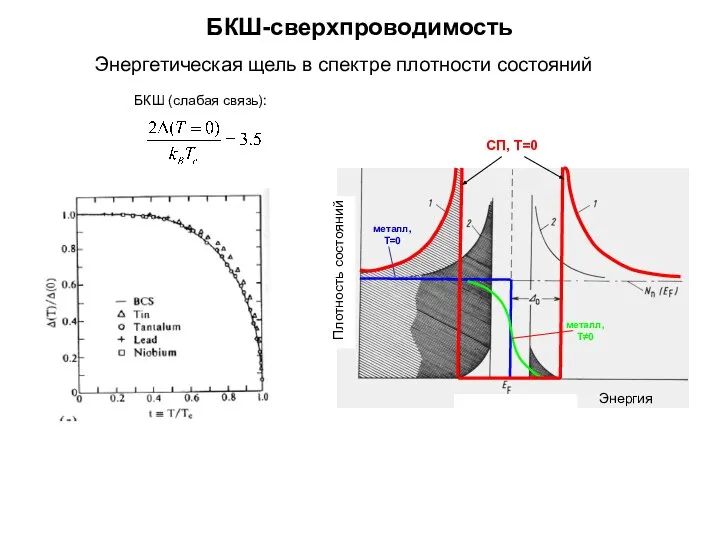 БКШ-сверхпроводимость. Терагерцовая оптика
БКШ-сверхпроводимость. Терагерцовая оптика ДМА – динамически механический анализ
ДМА – динамически механический анализ Механика. Кинематика
Механика. Кинематика Кинематика вращательного движения
Кинематика вращательного движения Инструменты, механизмы и технические устройства
Инструменты, механизмы и технические устройства Устройство и работа ДВС (двигателя внутреннего сгорания)
Устройство и работа ДВС (двигателя внутреннего сгорания) Смазка подшипниковых опор прокатных валков
Смазка подшипниковых опор прокатных валков Магнитный поток. Правило Ленца. Явление самоиндукции
Магнитный поток. Правило Ленца. Явление самоиндукции Энергия связи
Энергия связи Презентация на тему Кабинет физики
Презентация на тему Кабинет физики