Содержание
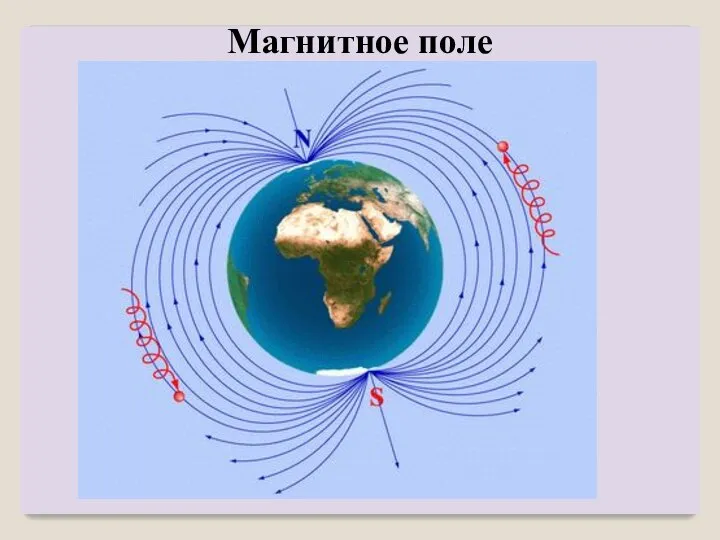
- 2. Магнитное поле
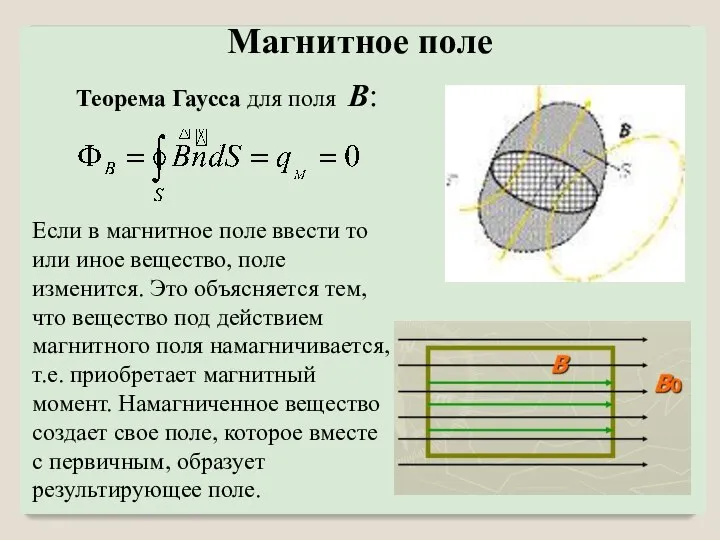
- 3. Теорема Гаусса для поля B: Если в магнитное поле ввести то или иное вещество, поле изменится.
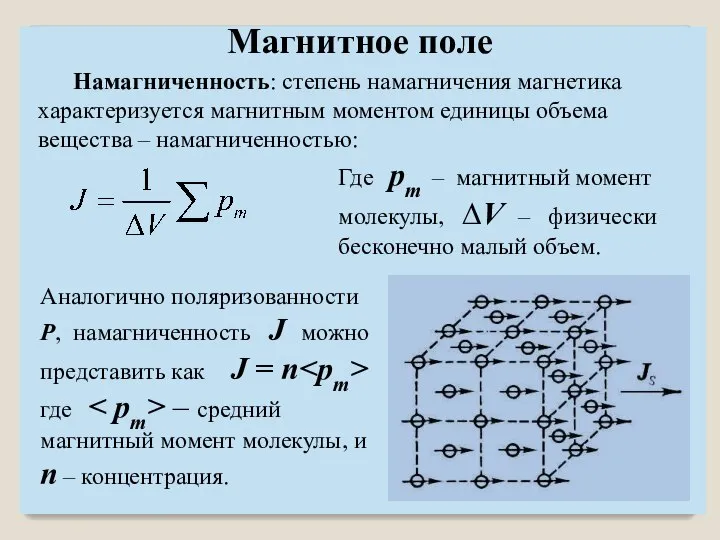
- 4. Намагниченность: степень намагничения магнетика характеризуется магнитным моментом единицы объема вещества – намагниченностью: Где pm – магнитный
- 5. J и pm имеют одинаковые направления ⇒ если J = 0 то и = 0. если
- 6. Связь B и H для линейных магнетиков: B = μ0(H + J) ⇒ B = μ0(1
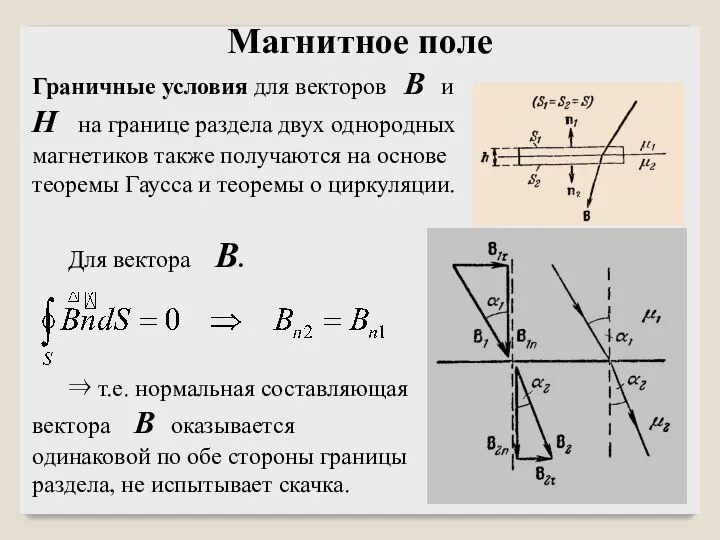
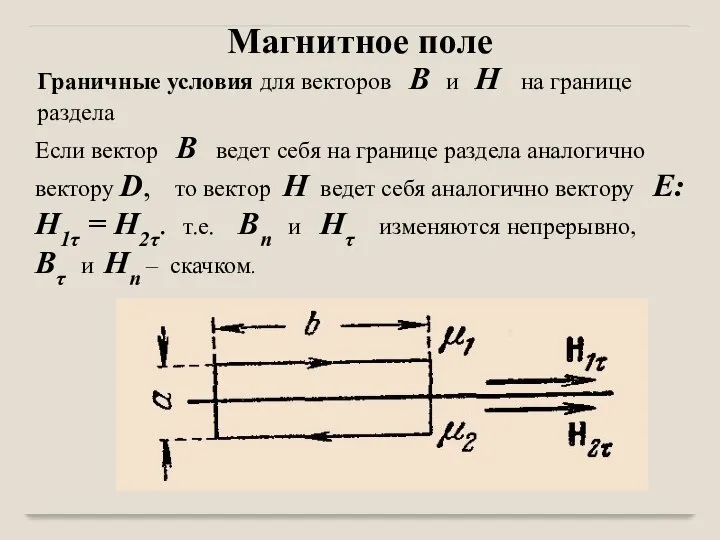
- 7. Граничные условия для векторов B и H на границе раздела двух однородных магнетиков также получаются на
- 8. Граничные условия для векторов B и H на границе раздела Если вектор B ведет себя на
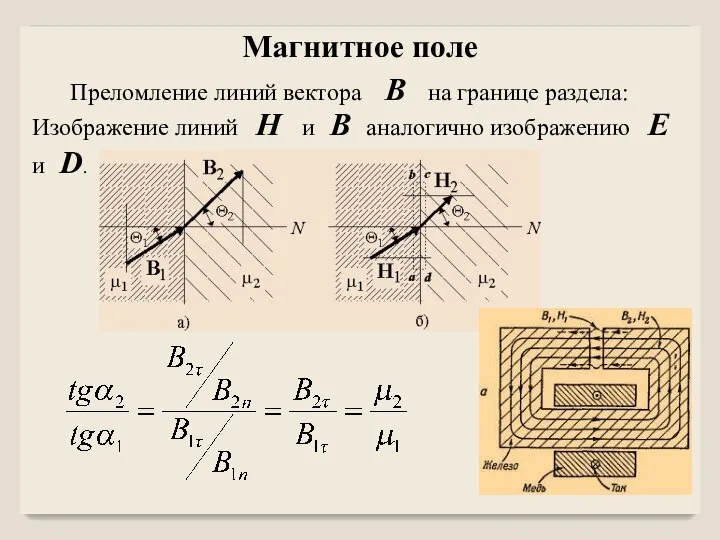
- 9. Магнитное поле Преломление линий вектора B на границе раздела: Изображение линий H и B аналогично изображению
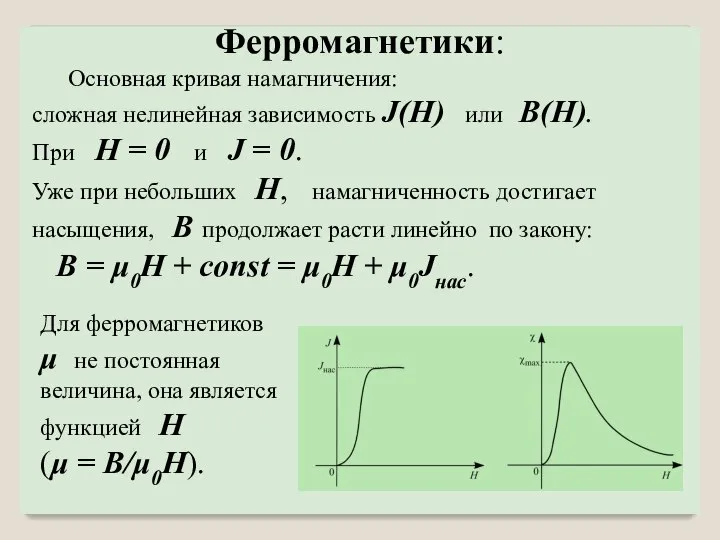
- 10. Основная кривая намагничения: сложная нелинейная зависимость J(H) или B(H). При H = 0 и J =
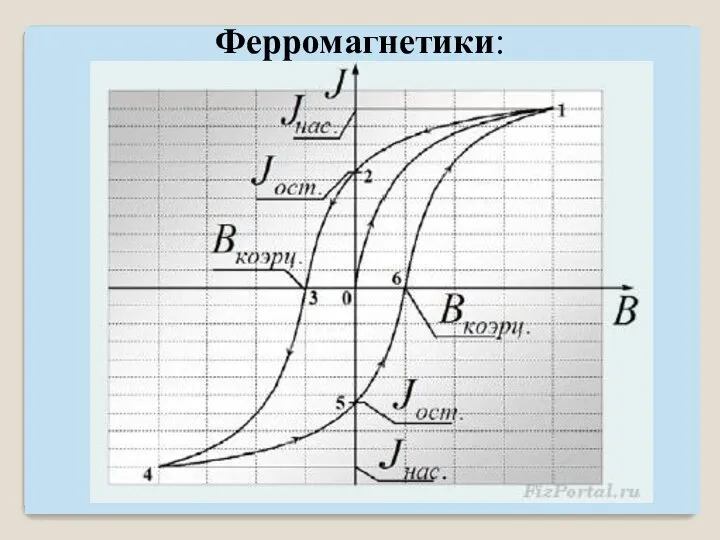
- 11. Гистерезис: Зависимость B(H) неоднозначная. Если ферромагнетик первоначально намагниченный до насыщения, затем поле H уменьшать от H1
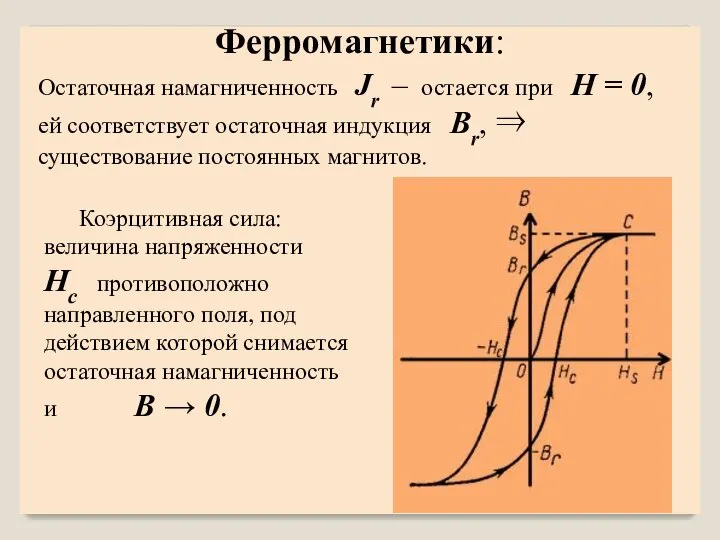
- 12. Остаточная намагниченность Jr – остается при H = 0, ей соответствует остаточная индукция Br, ⇒ существование
- 13. Ферромагнетики:
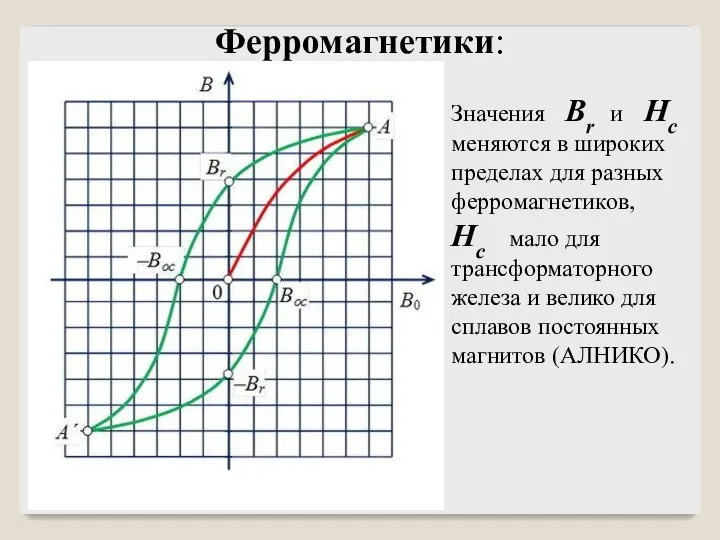
- 14. Значения Br и Hс меняются в широких пределах для разных ферромагнетиков, Hс мало для трансформаторного железа
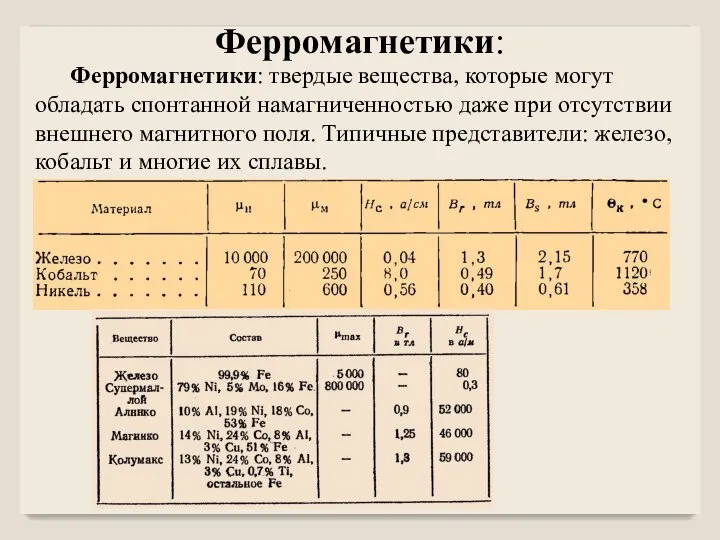
- 15. Ферромагнетики: твердые вещества, которые могут обладать спонтанной намагниченностью даже при отсутствии внешнего магнитного поля. Типичные представители:
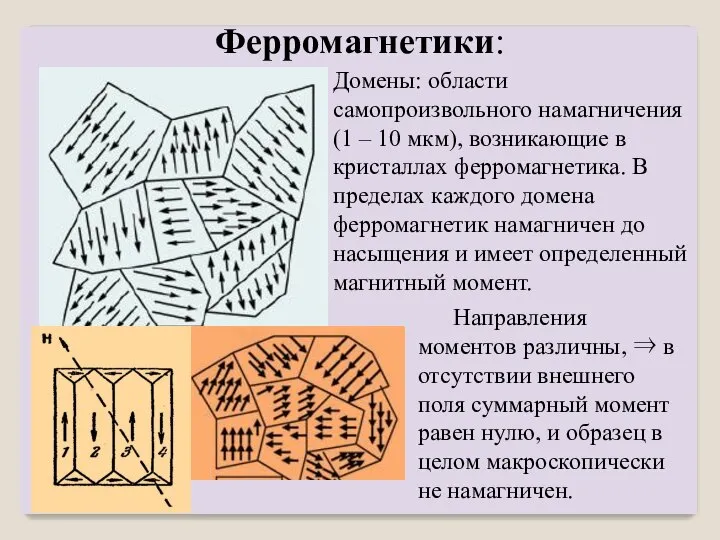
- 16. Домены: области самопроизвольного намагничения (1 – 10 мкм), возникающие в кристаллах ферромагнетика. В пределах каждого домена
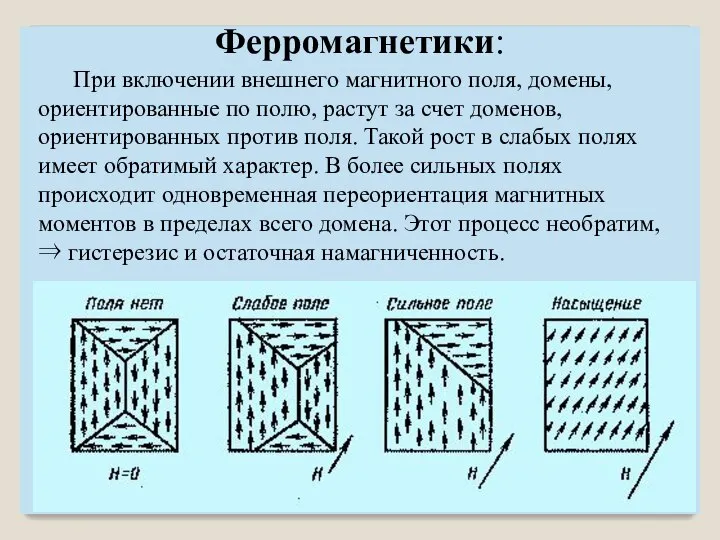
- 17. При включении внешнего магнитного поля, домены, ориентированные по полю, растут за счет доменов, ориентированных против поля.
- 18. При включении внешнего магнитного поля, домены, ориентированные по полю, растут за счет доменов, ориентированных против поля.
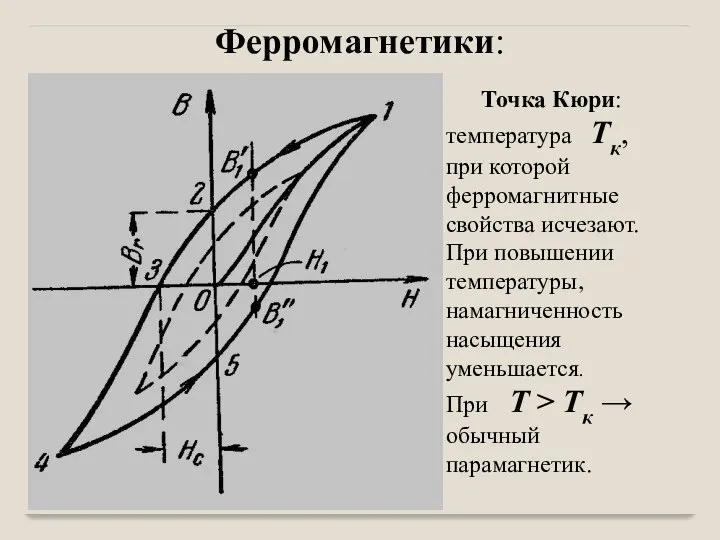
- 19. Точка Кюри: температура Tк, при которой ферромагнитные свойства исчезают. При повышении температуры, намагниченность насыщения уменьшается. При
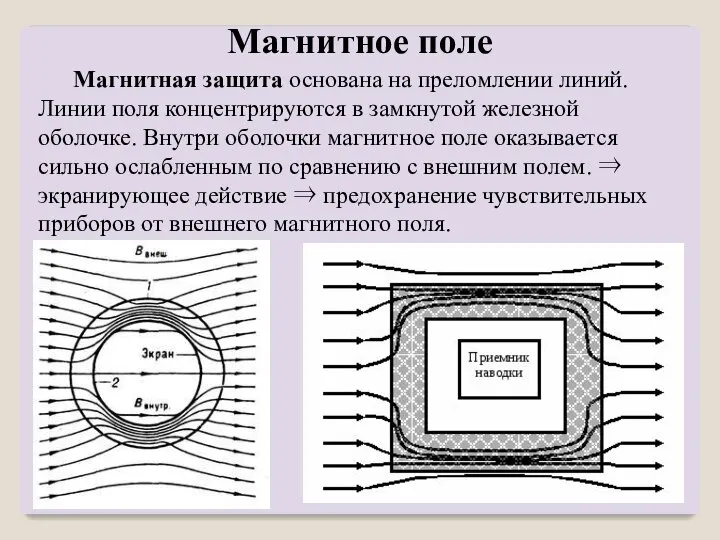
- 20. Магнитная защита основана на преломлении линий. Линии поля концентрируются в замкнутой железной оболочке. Внутри оболочки магнитное
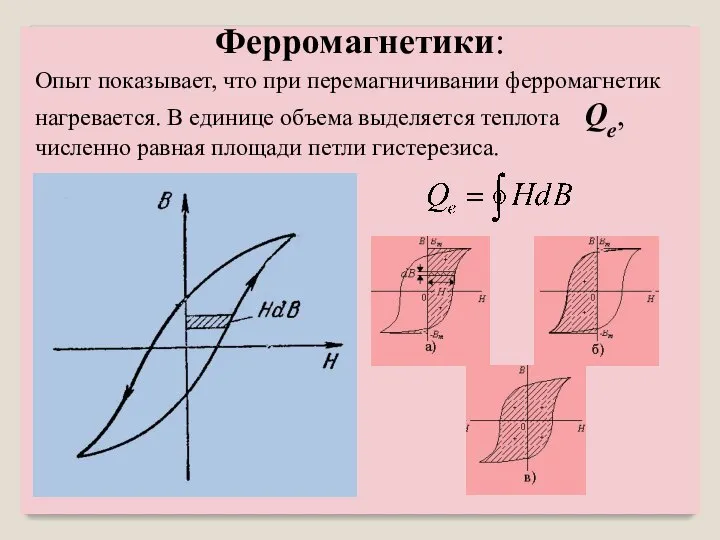
- 21. Опыт показывает, что при перемагничивании ферромагнетик нагревается. В единице объема выделяется теплота Qe, численно равная площади
- 22. В общей теории показывается, что энергию магнитного поля, как и в случае с электрическим полем, можно
- 23. Если зависимость B от H линейная, т.е. μ не зависит от H. Магнитная энергия – величина
- 24. Основные законы магнитного поля Теорема Гаусса: для поля B: Поток вектора B сквозь любую замкнутую поверхность
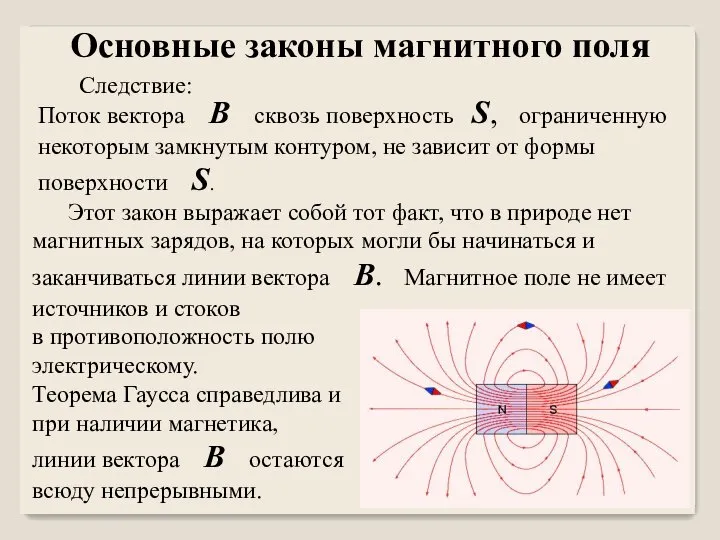
- 25. Следствие: Поток вектора B сквозь поверхность S, ограниченную некоторым замкнутым контуром, не зависит от формы поверхности
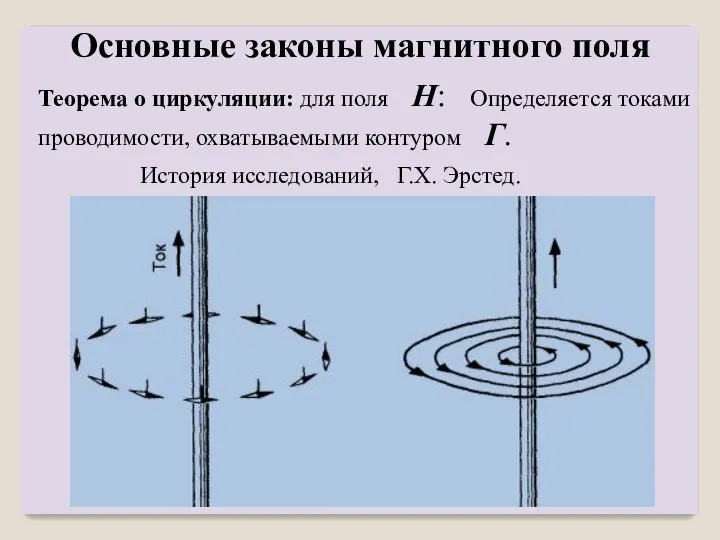
- 26. Теорема о циркуляции: для поля H: Определяется токами проводимости, охватываемыми контуром Γ. История исследований, Г.Х. Эрстед.
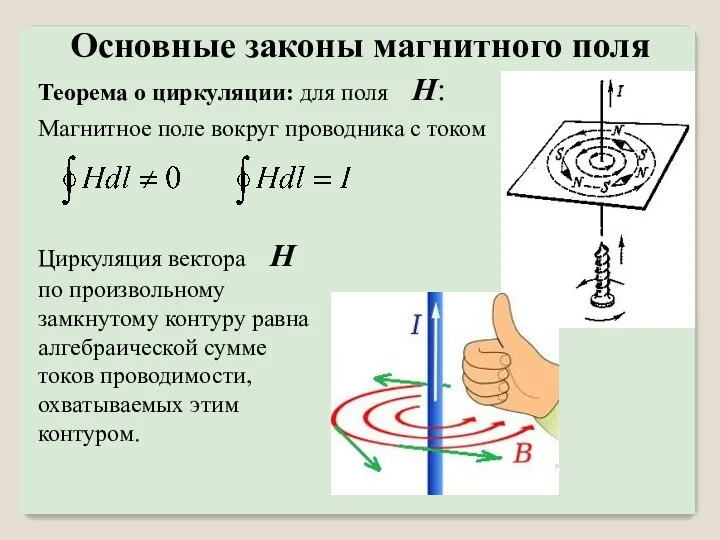
- 27. Теорема о циркуляции: для поля H: Магнитное поле вокруг проводника с током Циркуляция вектора H по
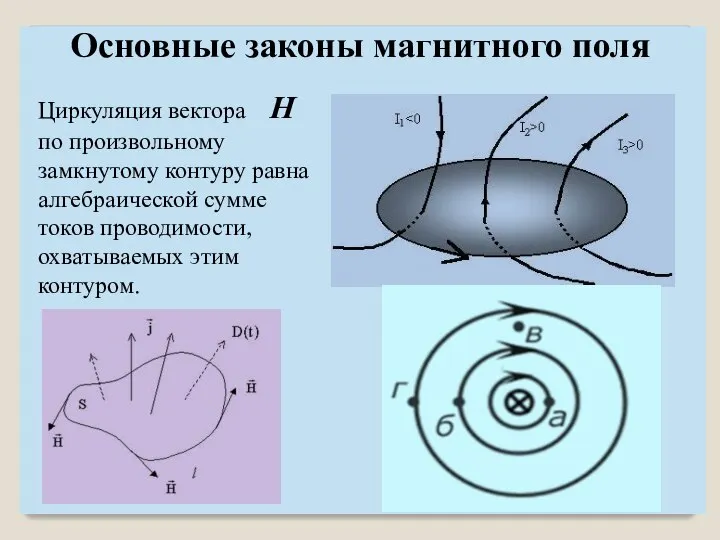
- 28. Основные законы магнитного поля Циркуляция вектора H по произвольному замкнутому контуру равна алгебраической сумме токов проводимости,
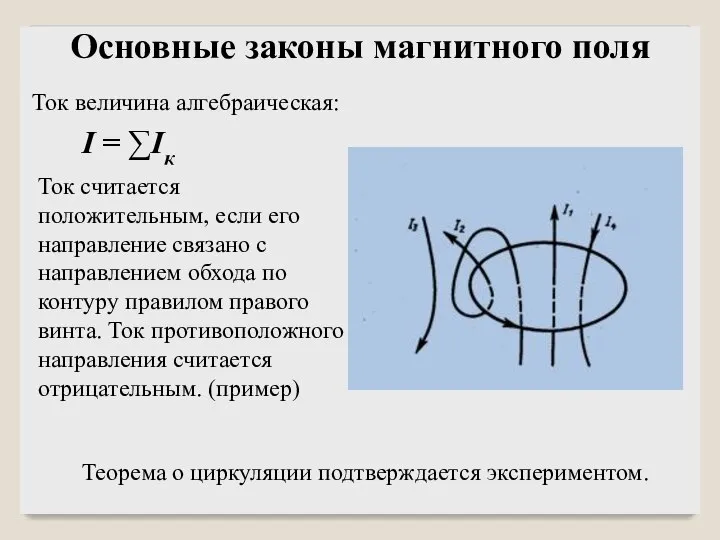
- 29. Основные законы магнитного поля Ток величина алгебраическая: I = ∑Iк Ток считается положительным, если его направление
- 30. Симметрия: Основные законы магнитного поля
- 31. Напряженность магнитного поля имеет размерность силы тока, деленной на длину. Единица измерения: ампер деленный на метр.
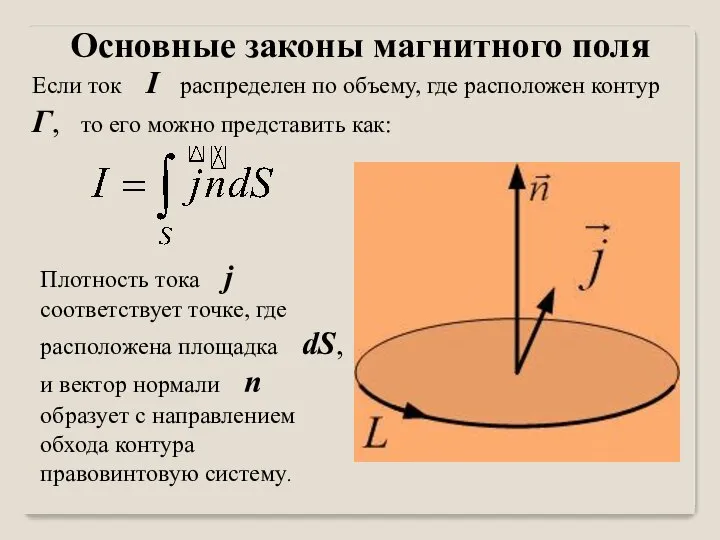
- 32. Если ток I распределен по объему, где расположен контур Γ, то его можно представить как: Плотность
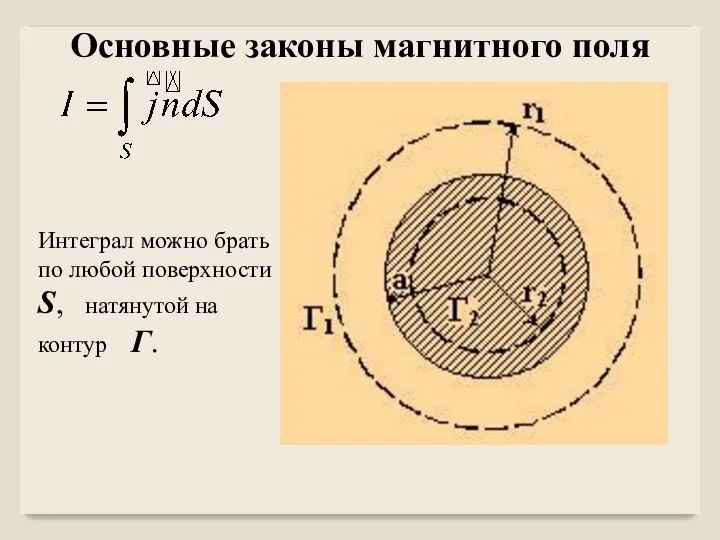
- 33. Интеграл можно брать по любой поверхности S, натянутой на контур Γ. Основные законы магнитного поля
- 34. Циркуляция вектора H, вообще не равна нулю, и этот факт означает. Что магнитное поле не потенциальное,
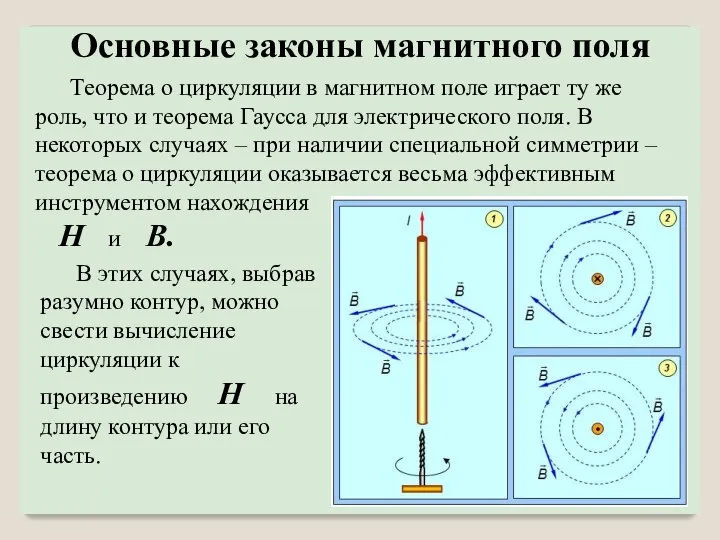
- 35. Теорема о циркуляции в магнитном поле играет ту же роль, что и теорема Гаусса для электрического
- 36. Пример: магнитное поле прямого тока: Провод прямой и бесконечный, сечение радиуса a, ток I. Линии поля
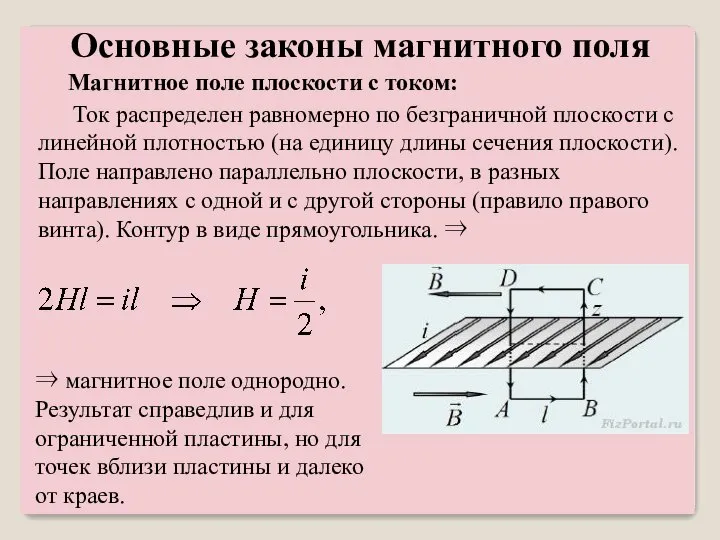
- 37. Магнитное поле плоскости с током: Ток распределен равномерно по безграничной плоскости с линейной плотностью (на единицу
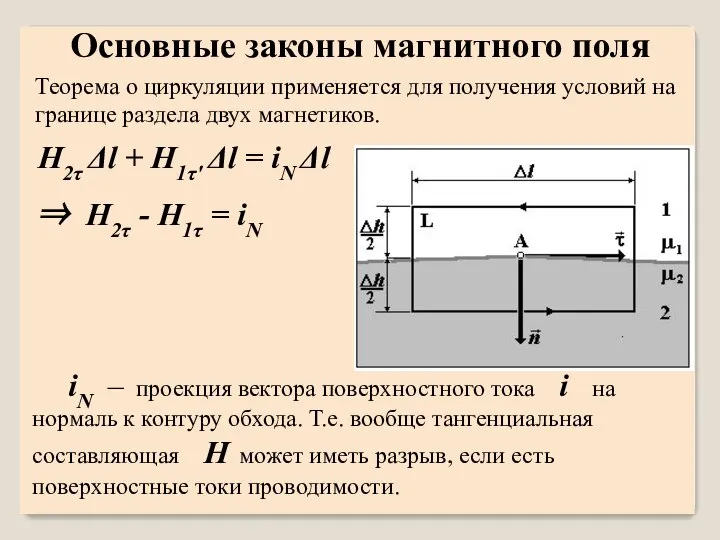
- 38. Теорема о циркуляции применяется для получения условий на границе раздела двух магнетиков. H2τ Δl + H1τʹ
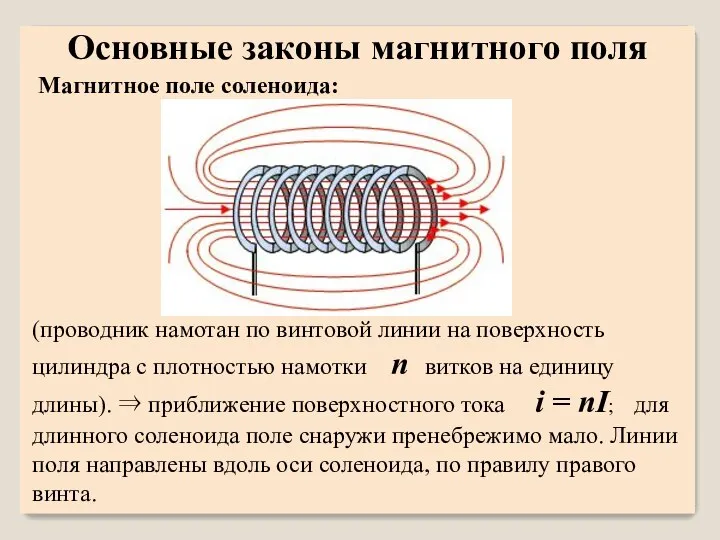
- 39. (проводник намотан по винтовой линии на поверхность цилиндра с плотностью намотки n витков на единицу длины).
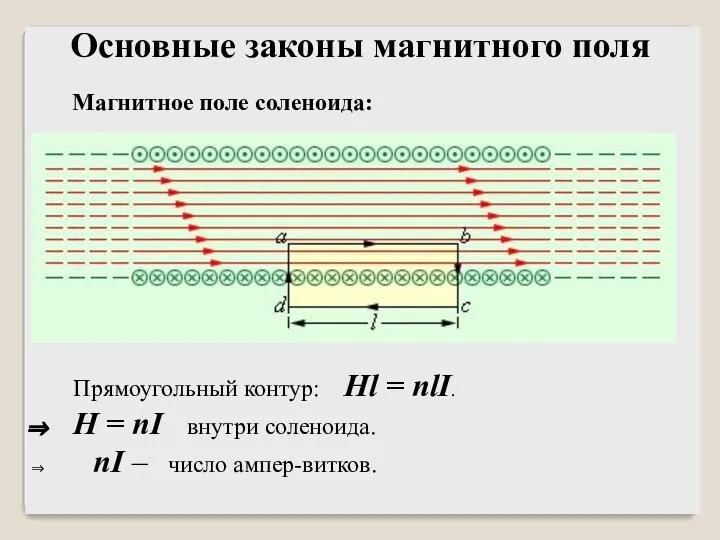
- 40. Прямоугольный контур: Hl = nlI. H = nI внутри соленоида. nI – число ампер-витков. Основные законы
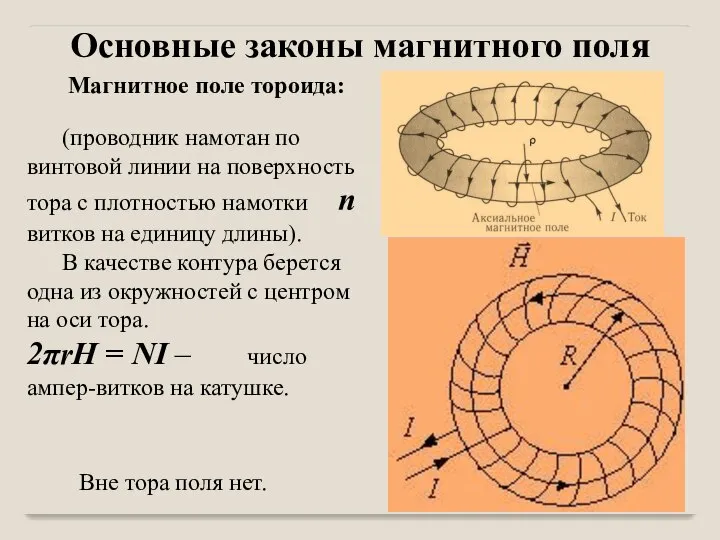
- 41. Магнитное поле тороида: (проводник намотан по винтовой линии на поверхность тора с плотностью намотки n витков
- 42. Дифференциальная форма законов магнитного поля. Теорема Гаусса Справедлива и для переменных полей. Теорема о циркуляции: Магнитное
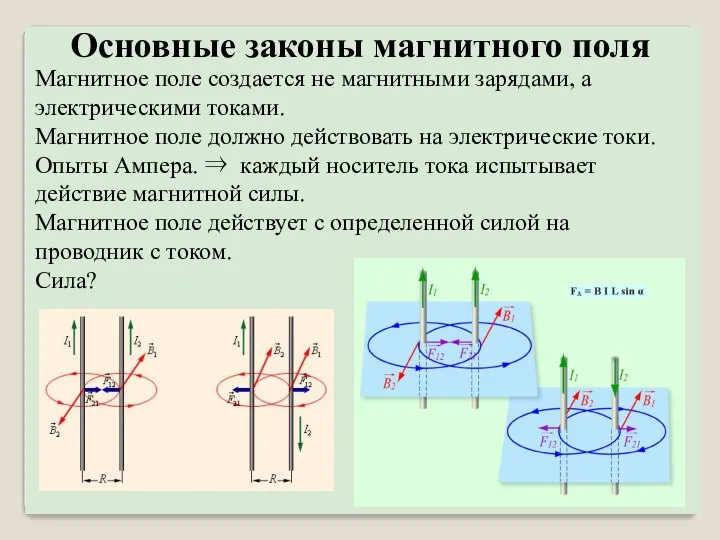
- 43. Магнитное поле создается не магнитными зарядами, а электрическими токами. Магнитное поле должно действовать на электрические токи.
- 44. Токи I1 и I2 одинаково направленные притягиваются, а противоположно направленные – отталкиваются, если действует только магнитная
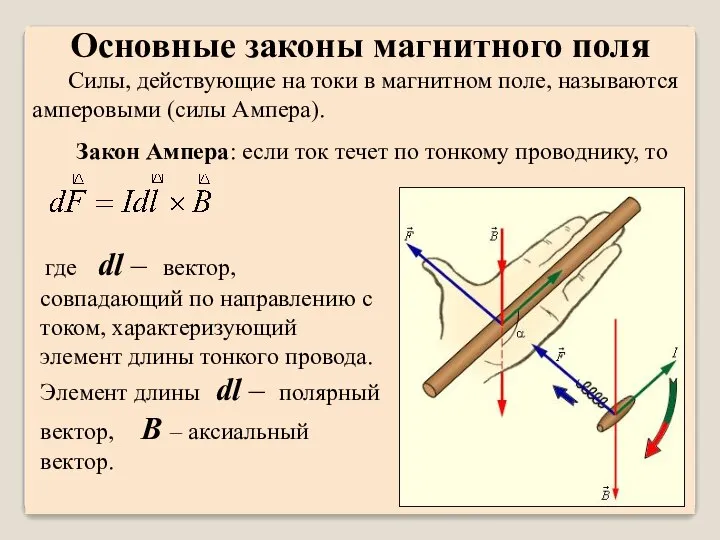
- 45. Силы, действующие на токи в магнитном поле, называются амперовыми (силы Ампера). Закон Ампера: если ток течет
- 46. Таким образом, Idl аналог q, а B – аналог E, т.е. силовым вектором магнитного поля становится
- 47. Единица измерения индукции B; Тесла [Тл]. Единица измерения μ0 Основные законы магнитного поля
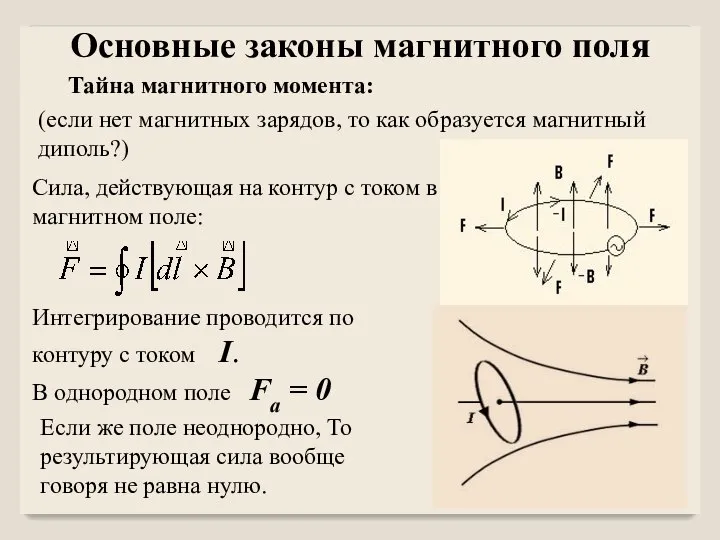
- 48. Тайна магнитного момента: (если нет магнитных зарядов, то как образуется магнитный диполь?) Сила, действующая на контур
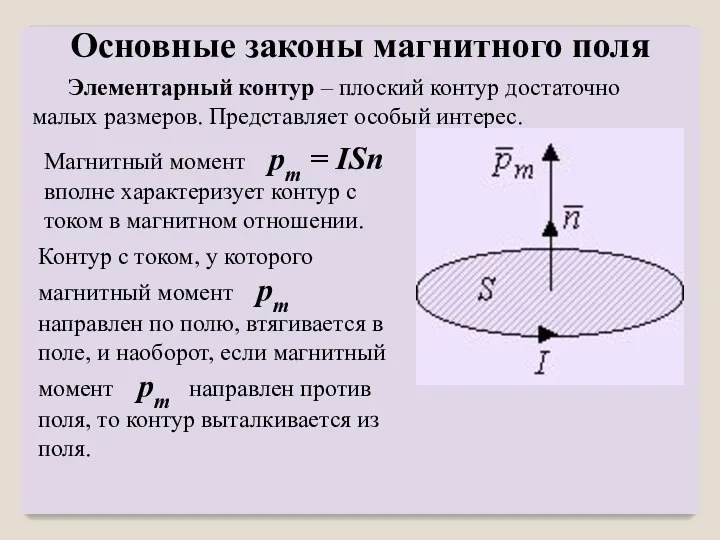
- 49. Элементарный контур – плоский контур достаточно малых размеров. Представляет особый интерес. Магнитный момент pm = ISn
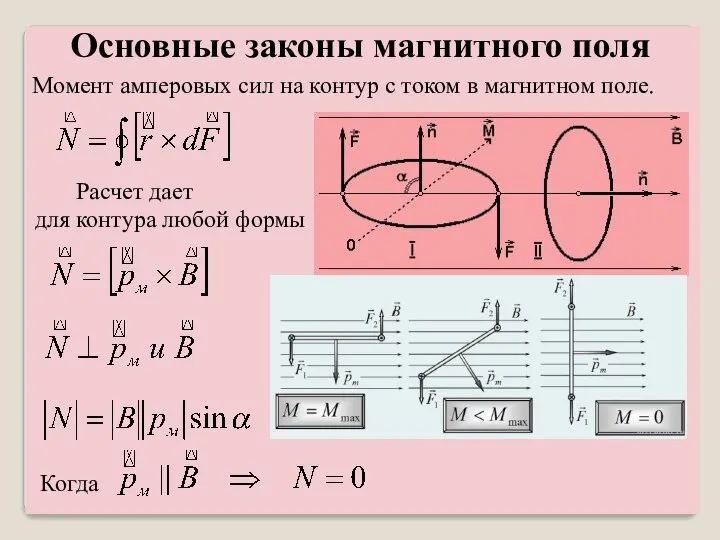
- 50. Момент амперовых сил на контур с током в магнитном поле. Расчет дает для контура любой формы
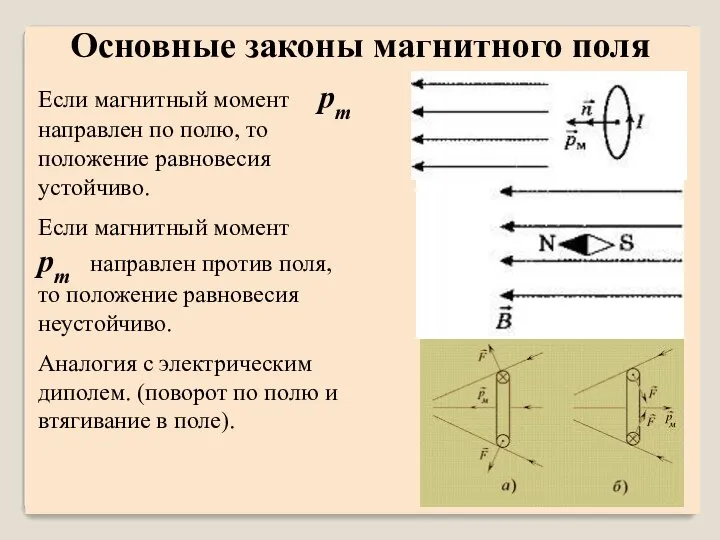
- 51. Если магнитный момент pm направлен по полю, то положение равновесия устойчиво. Если магнитный момент pm направлен
- 54. Скачать презентацию














![Единица измерения индукции B; Тесла [Тл]. Единица измерения μ0 Основные законы магнитного поля](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1108905/slide-46.jpg)

 Презентация 2
Презентация 2 Разработка стенда для исследования импульсных источников питания
Разработка стенда для исследования импульсных источников питания Поляризация света. Голография. Лекция 16-17
Поляризация света. Голография. Лекция 16-17 Физическая химия
Физическая химия Potential Flow Theory
Potential Flow Theory Презентация по физике "Скорость" -
Презентация по физике "Скорость" -  Диффузия. 7 класс
Диффузия. 7 класс АТОМНЫЕ ЭЛЕКТРОСТАНЦИИ С РЕАКТОРАМИ НА БЫСТРЫХ НЕЙТРОНАХ
АТОМНЫЕ ЭЛЕКТРОСТАНЦИИ С РЕАКТОРАМИ НА БЫСТРЫХ НЕЙТРОНАХ Ламинарное, равномерное движение жидкости в трубах. Лекция №6
Ламинарное, равномерное движение жидкости в трубах. Лекция №6 Електричне поле. Одна шз складових електромагнітого поля
Електричне поле. Одна шз складових електромагнітого поля Казкі астранаўта
Казкі астранаўта Получение радиоактивных изотопов и их применение
Получение радиоактивных изотопов и их применение Введение. Кинематика
Введение. Кинематика Молекулярно-кинетическая теория (МКТ) и термодинамика (лекция 5)
Молекулярно-кинетическая теория (МКТ) и термодинамика (лекция 5) Методики (методы) измерений
Методики (методы) измерений 7 кл Три состояния вещ-ва
7 кл Три состояния вещ-ва Ken Freese’s ’65 BJ-8 Piston Set DAMAGE. (29D motor)
Ken Freese’s ’65 BJ-8 Piston Set DAMAGE. (29D motor) Мгновенное превращение воды в лед
Мгновенное превращение воды в лед Кипение. Удельная теплота парообразования. Зависимость температуры кипения давления
Кипение. Удельная теплота парообразования. Зависимость температуры кипения давления Наблюдение сплошного и линейчатых спектров. Лабораторная работа
Наблюдение сплошного и линейчатых спектров. Лабораторная работа Точность измерений и вычислений
Точность измерений и вычислений Презентация на тему Равновесие тел
Презентация на тему Равновесие тел  Презентация на тему Путь. Перемещение. Координаты движущегося тела
Презентация на тему Путь. Перемещение. Координаты движущегося тела  Презентация на тему Магнитные свойства вещества (11 класс)
Презентация на тему Магнитные свойства вещества (11 класс)  c38d9b8
c38d9b8 Производная в физике и технике
Производная в физике и технике Презентация на тему Физика в картинках
Презентация на тему Физика в картинках  Загальні закономірності горіння газоповітряних систем (тема 7)
Загальні закономірності горіння газоповітряних систем (тема 7)