близко к частоте собственных колебаний, фактически может совпадать, но это не всегда так и не является причиной резонанса.
В результате резонанса при некоторой частоте вынуждающей силы колебательная система оказывается особенно отзывчивой на действие этой силы. Степень отзывчивости в теории колебаний описывается величиной, называемой добротностью. При помощи резонанса можно выделить и/или усилить даже весьма слабые периодические колебания.
Наиболее известная большинству людей механическая резонансная система — это обычные качели. Если вы будете подталкивать качели в соответствии с их резонансной частотой, размах движения будет увеличиваться, в противном случае движения будут затухать. Резонансную частоту такого маятника с достаточной точностью в диапазоне малых смещений от равновесного состояния, можно найти по формуле:
, где g это ускорение свободного падения (9,8 м/с² для поверхности Земли), а L — длина от точки подвешивания маятника до центра его масс. (Более точная формула довольно сложна, и включает эллиптический интеграл). Важно, что резонансная частота не зависит от массы маятника. Также важно, что раскачивать маятник нельзя на кратных частотах (высших гармониках), зато это можно делать на частотах, равных долям от основной (низших гармониках).
Резонанс.



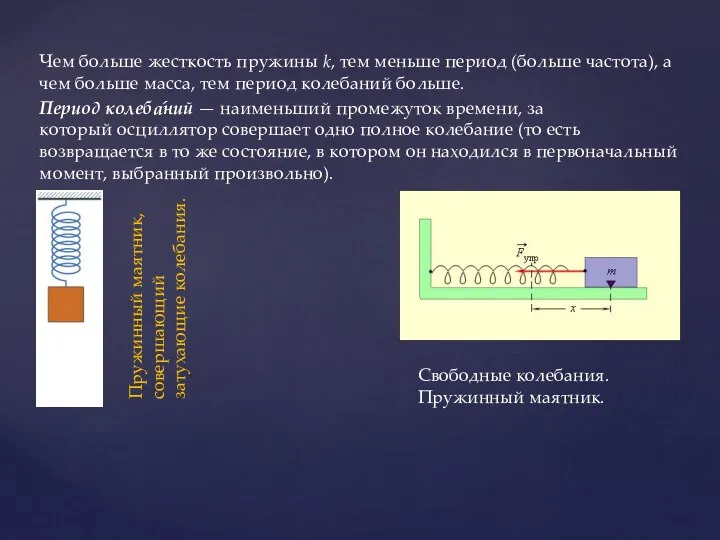



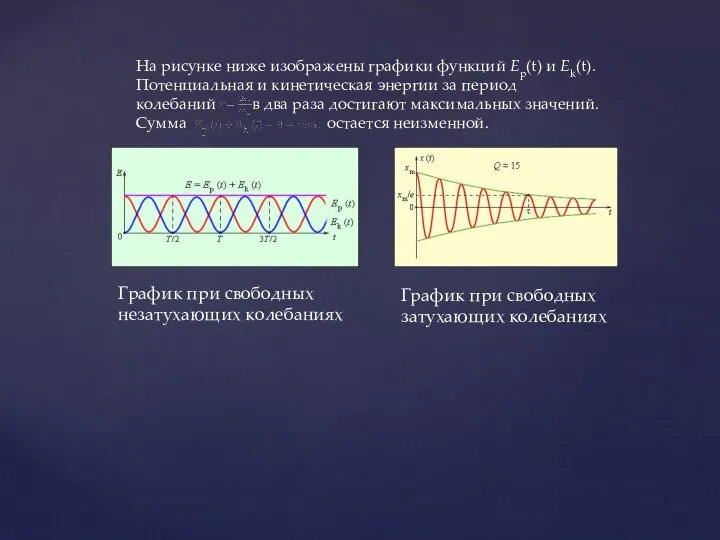



 Магнитные материалы и компоненты. (Лекция 5)
Магнитные материалы и компоненты. (Лекция 5) Грунтосмесительные машины
Грунтосмесительные машины Урок по физике 8 класс Букарева Т.П., учитель физики и информатики МБОУ «Средняя общеобразовательная школа №2 г. Медногорска
Урок по физике 8 класс Букарева Т.П., учитель физики и информатики МБОУ «Средняя общеобразовательная школа №2 г. Медногорска Связь между давлением и объемом газа при постоянной температуре
Связь между давлением и объемом газа при постоянной температуре Последовательное и параллельное соединение потребителей (сопротивлений)
Последовательное и параллельное соединение потребителей (сопротивлений) Парогенератор. Оболочка ТВЕЛа
Парогенератор. Оболочка ТВЕЛа История создания швейной машины
История создания швейной машины Использование электромагнитов
Использование электромагнитов Исследование параметров и характеристик полупроводниковых диодов. Лабораторная работа
Исследование параметров и характеристик полупроводниковых диодов. Лабораторная работа Закон сохранения энергии в биомеханике
Закон сохранения энергии в биомеханике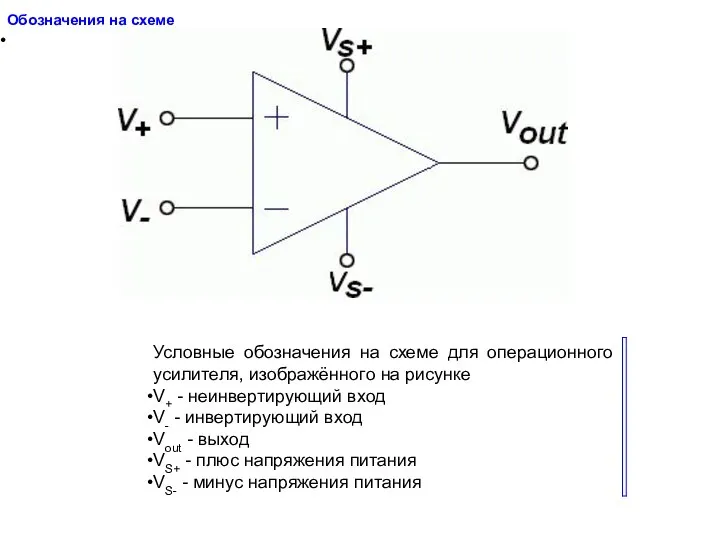 Обозначения на схеме
Обозначения на схеме Второй закон Ньютона, масса
Второй закон Ньютона, масса Нанотехнологии и их применение
Нанотехнологии и их применение Техническое обслуживание и ремонт систем, узлов, приборов автомобилей
Техническое обслуживание и ремонт систем, узлов, приборов автомобилей Техническая учеба по теме: Продольная дифференциальная защита линий
Техническая учеба по теме: Продольная дифференциальная защита линий Удельная теплоёмкость
Удельная теплоёмкость Презентация на тему Энергосберегающие лампы
Презентация на тему Энергосберегающие лампы  Коронная передача
Коронная передача Газоразрядные приборы
Газоразрядные приборы Приборы для измерения давления
Приборы для измерения давления Теплофизические свойства полимеров
Теплофизические свойства полимеров Методы и приборы для измерения влажности газовых сред
Методы и приборы для измерения влажности газовых сред силы
силы Роль света в жизни человека
Роль света в жизни человека Ядерная программа Ирана
Ядерная программа Ирана сила Архимеда сила выталкивающая тело из жидкости
сила Архимеда сила выталкивающая тело из жидкости Структурные схемы приборов для регистрации ионизирующего излучения
Структурные схемы приборов для регистрации ионизирующего излучения Закон сохранения импульса
Закон сохранения импульса