Содержание
- 2. В «мелкой» яме существует только одно чётное решение Условия сшивки Уравнение для энергии Уравнение для энергии
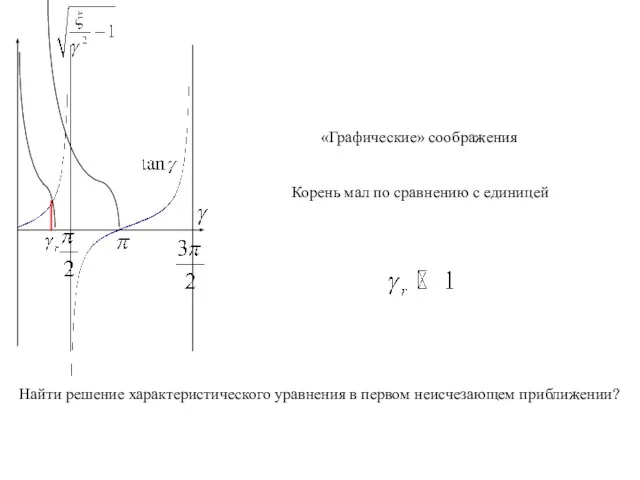
- 3. «Графические» соображения Найти решение характеристического уравнения в первом неисчезающем приближении? Корень мал по сравнению с единицей
- 4. Решение Или Найти энергию в первом неисчезающем приближении при
- 5. Решение с точностью до линейного слагаемого Или, возвращаясь к исходным обозначениям Является ли ответ физически значимым?
- 6. Условия сшивки при нулевой энергии Надо искать решение с точностью до квадратичных слагаемых
- 7. Решение с точностью до квадратичных слагаемых Полезная формула Поэтому Или Энергия связанного состояния в мелкой яме
- 8. В том же приближении найти волновую функцию связанного состояния? Указание. Оценить величины и записать условия сшивки
- 9. Волновая функция частицы в «мелкой» яме во всём интервале изменения координаты Условия сшивки для «мелкой ямы
- 10. Волновая функция частицы в «мелкой» яме во всём интервале изменения координаты Задачи. 1. Вычислить средние значения
- 11. 1. Вычислить средние значения кинетической и потенциальной энергии частицы в мелкой яме. Среднее значение кинетической энергии
- 12. Из семинара о дельта-функции
- 13. Среднее значение кинетической энергии частицы в мелкой яме (продолжение) Вычислить интегралы?
- 14. Среднее значение кинетической энергии частицы в мелкой яме (продолжение) Интегралы
- 15. Среднее значение потенциальной энергии частицы в мелкой яме. Сравнить величины средних значений кинетической и потенциальной энергий?
- 16. Отношение средних значений кинетической и потенциальной энергий
- 17. Найти плотность распределения вероятности для импульса частицы в мелкой яме. Используя принцип суперпозиции, записать в явном
- 18. Волновая функция в импульсном представлении Связанное состояние в «мелкой» яме
- 20. Скачать презентацию
















 Экологического воспитание на уроках физики и во внеурочное время
Экологического воспитание на уроках физики и во внеурочное время Конкурс Что за формула?
Конкурс Что за формула? Théorèmes généraux
Théorèmes généraux Индивидуальны й учебный проект по дисциплине физика
Индивидуальны й учебный проект по дисциплине физика Маятниковые копры
Маятниковые копры Метапредметный подход в преподавании физики
Метапредметный подход в преподавании физики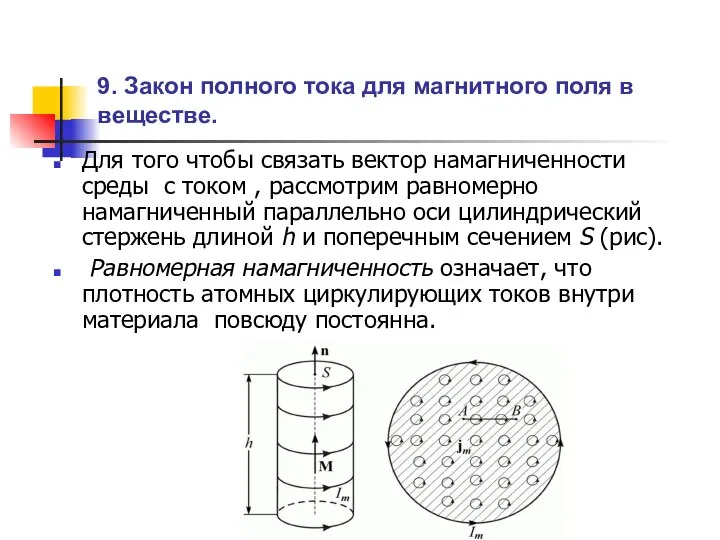 Закон полного тока для магнитного поля в веществе
Закон полного тока для магнитного поля в веществе Пояснения излучения
Пояснения излучения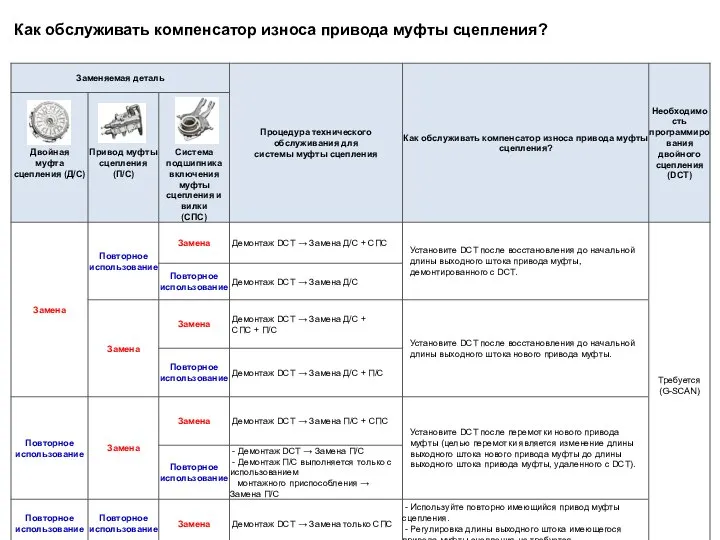 Как обслуживать компенсатор износа привода муфты сцепления
Как обслуживать компенсатор износа привода муфты сцепления Три состояния вещества
Три состояния вещества Метод переходного состояния. Классическая теория
Метод переходного состояния. Классическая теория Строение вещества, атома
Строение вещества, атома Электромагнитные волны
Электромагнитные волны Механическая работа и мощность
Механическая работа и мощность Общие сведения о системах первичного электроснабжения РЭС
Общие сведения о системах первичного электроснабжения РЭС Перспективы применения мономолекулярных магнитов (МMM) (single molecule magnets – SMM)
Перспективы применения мономолекулярных магнитов (МMM) (single molecule magnets – SMM) Раскачивание мостов. Процесс синхронизации
Раскачивание мостов. Процесс синхронизации Презентация
Презентация Квантовая криптография
Квантовая криптография Воздухораспределитель №242
Воздухораспределитель №242 История развития телевидения
История развития телевидения График плавления и отвердевания кристаллических тел
График плавления и отвердевания кристаллических тел Фотоэффект. (11 класс)
Фотоэффект. (11 класс)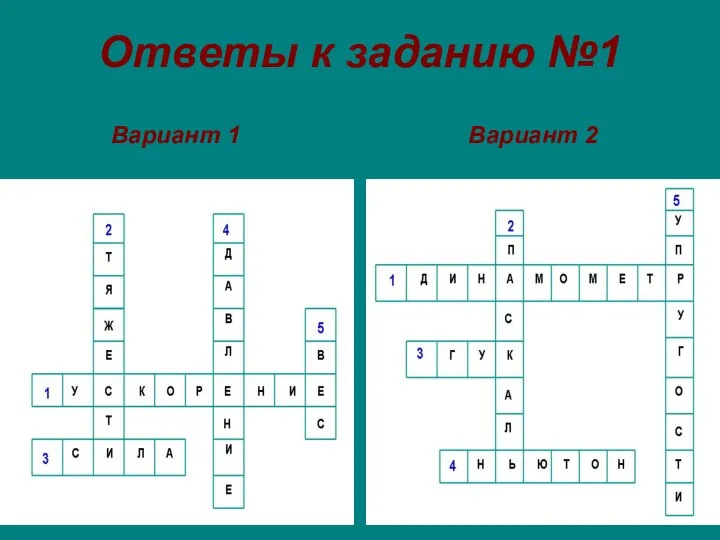 Сила трения. Ответы к заданию №1
Сила трения. Ответы к заданию №1 Обобщение пройденного. Подготовка к контрольной работе №1
Обобщение пройденного. Подготовка к контрольной работе №1 Закон Ома для участка цепи
Закон Ома для участка цепи Рассеивающие линзы
Рассеивающие линзы Применение ядерной энергии для преобразования ее в электрическую энергию
Применение ядерной энергии для преобразования ее в электрическую энергию