Содержание
- 2. Случайная величина: переменная, которая может принимать любое значение из заданного множества, при этом с ней связана
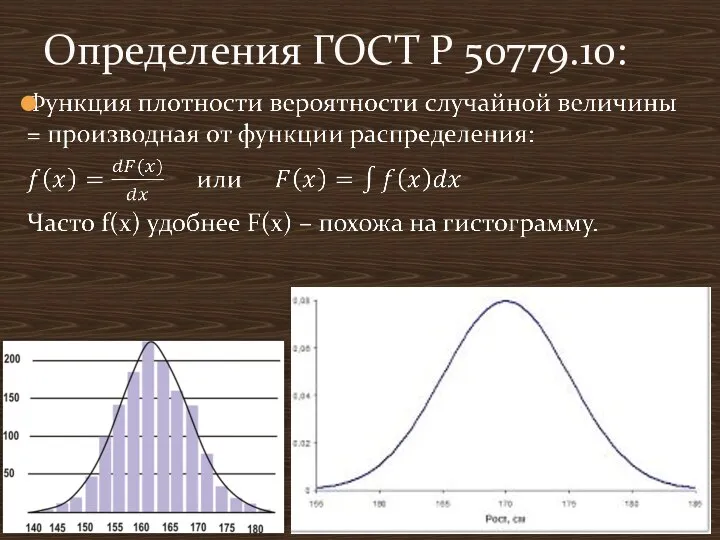
- 3. Определения ГОСТ Р 50779.10:
- 4. Генеральная совокупность – множество всех значений случайной величины. В метрологии – гипотетический объект, например, бесконечное множество
- 5. Результаты измерений представляют собой выборку. Задача – по выборке определить характеристики генеральной совокупности. Определения (рабоче-крестьянские): Генеральная
- 6. Характеристики непрерывного распределения:
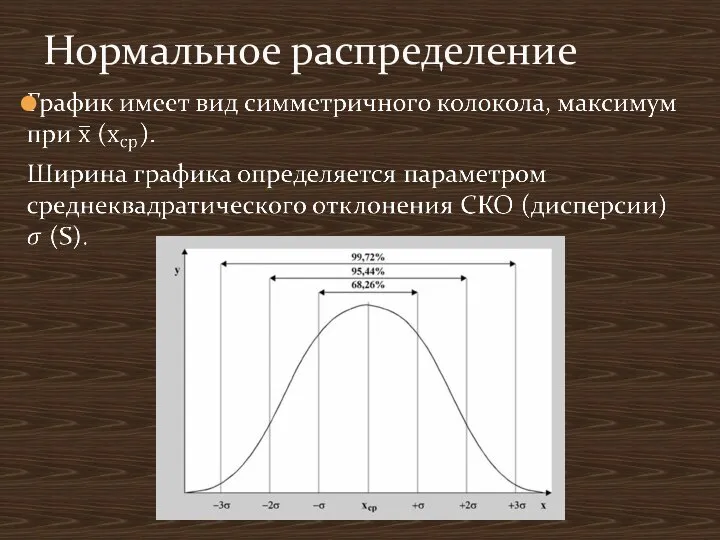
- 7. Нормальное распределение
- 8. Простейшая модель: результат измерения = истинное значение измеряемой величины + случайная величина с М=0 и нормальным
- 9. - нахождение параметров ГС по имеющейся выборке. Точечная оценка – оценка одним числом. Интервальная оценка –
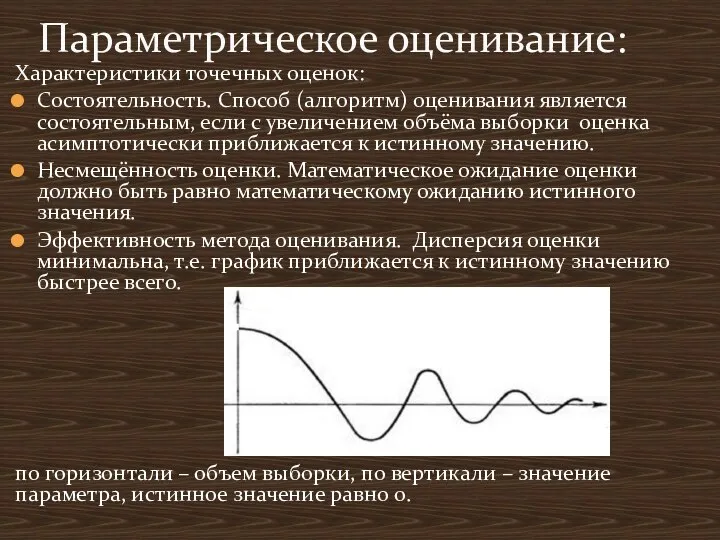
- 10. Характеристики точечных оценок: Состоятельность. Способ (алгоритм) оценивания является состоятельным, если с увеличением объёма выборки оценка асимптотически
- 11. Точечное оценивание
- 12. . Нормальное распределение Подчиняются ли результаты измерений нормальному закону распределения - в каждом опыте нужно решать
- 13. . Равномерное (прямоугольное) распределение
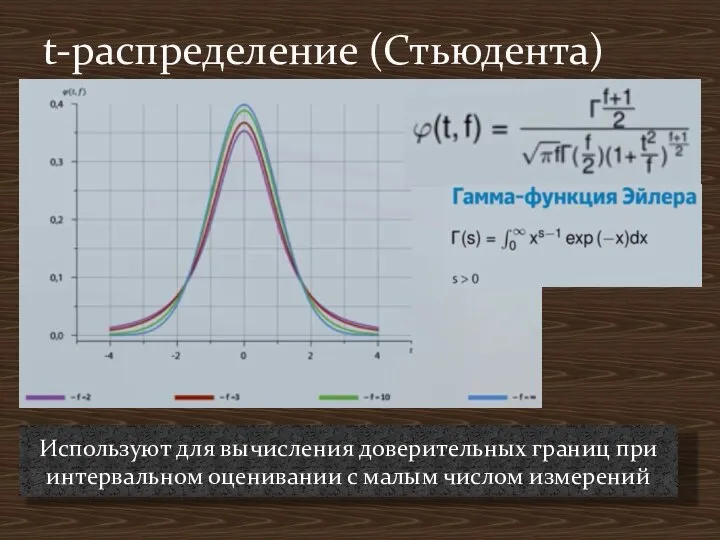
- 14. . t-распределение (Стьюдента) Используют для вычисления доверительных границ при интервальном оценивании с малым числом измерений
- 15. Вариант 1: ГС имеет нормальное распределение, известно его СКО. Оценить результат n многократных измерений и определить
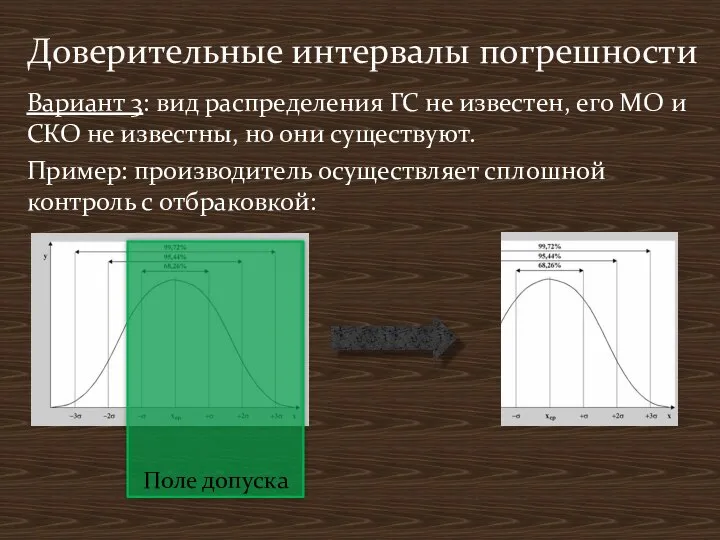
- 16. Вариант 3: вид распределения ГС не известен, его МО и СКО не известны, но они существуют.
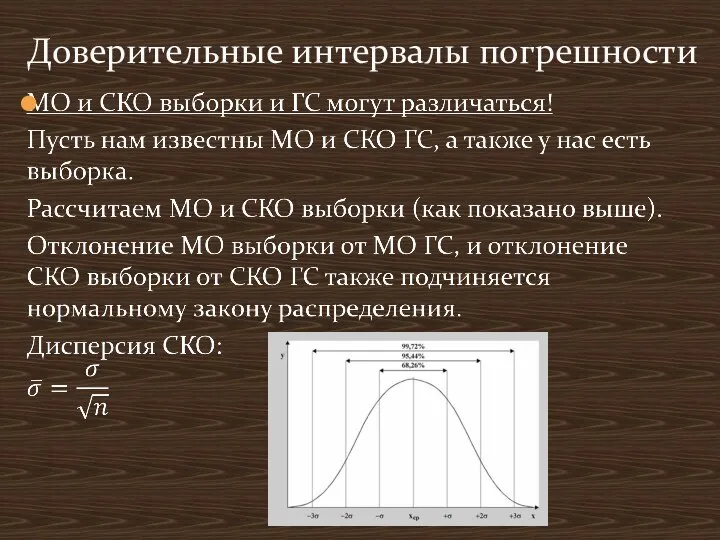
- 17. Доверительные интервалы погрешности
- 18. Доверительные интервалы погрешности
- 19. ГОСТ Р 8.736-2011. ГСИ. Измерения прямые многократные. Методы обработки результатов измерений. Основные положения Дано: результаты измерений
- 20. Среднее арифметическое исправленных результатов: СКО результатов измерений Дальнейшие расчёты носят вероятностный характер. Обычно принимаем q=5% (все
- 21. Критерий Граббса Исключение грубых погрешностей
- 22. Проверяем, что результаты измерений подчиняются нормальному распределению: при n больше 50 – критерий Пирсона или Мизеса-Смирнова
- 23. Критерий 1. Результаты измерений распределены по нормальному закону, если: Проверка выборки на нормальность
- 24. Критерий 2. Результаты измерений распределены по нормальному закону, если не больше m разностей превзошли произведение Проверка
- 25. находят в виде *Если распределение результатов измерений не является нормальным – этот и дальнейшие расчёты делать
- 26. Неисключённая систематическая погрешность (НСП) образуется из составляющих НСП: метода; средства измерений; других источников. 1. При хорошем
- 27. Доверительные границы погрешности оценки измеряемой величины: В случаях (1) и (2) – см. предыдущий слайд ,
- 28. Итоговый результат
- 29. Результаты измерения диаметра вала (30 значений) 8.736 измерения пример.xlsx Измерения проведены микрометром, погрешность средства измерения =
- 30. 3) найдём максимальное и минимальное измеренные значения =МАКС(A1:A30) =МИН(A1:A30) =20,81 =19,62 4) Вычислим критерии Граббса: G1=3,9681
- 31. Пример:
- 32. Пример:
- 34. Скачать презентацию

























 Презентация на тему Основоположники физики
Презентация на тему Основоположники физики  Характеристика твердого состояния вещества. Упругие свойства твердых тел. Закон Гука
Характеристика твердого состояния вещества. Упругие свойства твердых тел. Закон Гука Параллельный перенос сил. Связи и их реакции. Уравнения равновесия
Параллельный перенос сил. Связи и их реакции. Уравнения равновесия Лед и соль!
Лед и соль! Радиоактивность в жизни современного человека, значения ядерной энергетики
Радиоактивность в жизни современного человека, значения ядерной энергетики Презентация на тему Теория относительности и Альберт Эйнштейн
Презентация на тему Теория относительности и Альберт Эйнштейн  Физическая викторина. Игра
Физическая викторина. Игра Сборка электрической цепи и измерение силы тока
Сборка электрической цепи и измерение силы тока Подготовка к контрольной работе №2. Динамика
Подготовка к контрольной работе №2. Динамика Электромонтажные и сборочные технологии
Электромонтажные и сборочные технологии Презентация на тему Атмосферное давление
Презентация на тему Атмосферное давление  Сила Лоренца
Сила Лоренца Соединения фитингами
Соединения фитингами Теоретическая механика
Теоретическая механика Что изучает физика
Что изучает физика Методы расчетов резисторных схем постоянного тока.11 класс
Методы расчетов резисторных схем постоянного тока.11 класс Наблюдение интерференции и дифракции свет
Наблюдение интерференции и дифракции свет Механические свойства твердых тел
Механические свойства твердых тел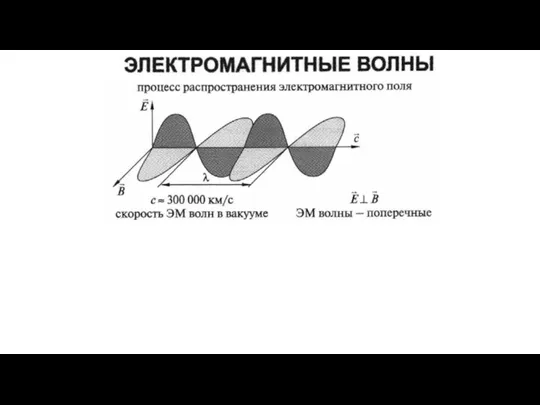 Электромагнитные волны
Электромагнитные волны Конденсаторы
Конденсаторы Презентация на тему Единица электрического заряда
Презентация на тему Единица электрического заряда  Элементы теории относительности
Элементы теории относительности Механическое движение
Механическое движение Движение под углом к горизонту
Движение под углом к горизонту Изучение процессов поглощения энергии при испарении жидкости и выделения ее при конденсации пара
Изучение процессов поглощения энергии при испарении жидкости и выделения ее при конденсации пара Кипение воды
Кипение воды Отражение света
Отражение света Плавание тел. Условие плавания тел
Плавание тел. Условие плавания тел