Презентация Механика Лекция 1

2. Модели в механике. Система отсчета. Материальная точка. Траектория, длина пути. Вектор перемещения.
Механическое движение – изменение положения тела относительно других тел с течением времени.
Для описания движения тел, в зависимости от условий конкретных задач, в механике используются различные физические модели, в которых из всего многообразия проявлений движения выделены главные, определяющие характер движения. Простейшей моделью является материальная точка.
Материальная точка – это модель тела, размерами и формой которого можно пренебречь по сравнению с масштабами движения.

2. Модели в механике. Система отсчета. Материальная точка. Траектория, длина пути. Вектор перемещения.
При взаимодействии тел друг с другом они могут деформироваться, то есть изменять свою форму и размеры. Поэтому в механике вводится еще одна модель – абсолютно твердое тело. Абсолютно твердым телом называется тело, которое ни при каких условиях не может деформироваться, и при всех условиях расстояние между двумя частицами этого тела остается постоянным.
Любое движение твердого тела можно представить как комбинацию поступательного и вращательного движения. Поступательное движение – это движение, при котором любая прямая жестко связанная с движущимся телом, остается параллельной своему первоначальному положению. Вращательное движение – это движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной прямой, называемой осью вращения.

2. Модели в механике. Система отсчета. Материальная точка. Траектория, длина пути. Вектор перемещения.
Движение тел происходит в пространстве и во времени. Поэтому для описания движения материальной точки надо знать, в каких местах пространства эта точка находилась и в какие моменты времени она проходила то или иное положение.
Тела отсчета – тела, относительно которых определяется или изучается положение данного движущегося тела.
Система отсчета – это тело отсчета, связанная с ним система координат и способ измерения времени (часы).
Траектория – линия, которую описывает материальная точка в пространстве при движении. В зависимости от формы траектории движение может прямолинейным и криволинейным.
Расстояние, пройденное телом, с момента начала отсчета времени, называется длиной пути. Это длина траектории. Обозначения: L, S, ΔS.

2. Модели в механике. Система отсчета. Материальная точка. Траектория, длина пути. Вектор перемещения.
Вектор, соединяющий начальное положение с последующим положением, называют перемещением. Обозначения:
Вектор, соединяющий некоторую фиксированную точку пространства с данной движущейся точкой, называется радиус-вектором.

2. Модели в механике. Система отсчета. Материальная точка. Траектория, длина пути. Вектор перемещения.
В декартовой системе координат, используемой наиболее часто, положение точки в данный момент времени по отношению к этой системе характеризуется тремя координатами x, y, z или радиусом-вектором. При этом проекции радиуса-вектора на оси системы отсчета эквивалентны координатам материальной точки x, y, z:
При движении материальной точки ее координаты с течением времени изменяются. Уравнение движения материальной точки может быть задано 3-мя способами:

3. Кинематика материальной точки.
Скорость и ускорение точки.
Кинематика – это раздел механики, изучающий движение тел без учета взаимодействия, то есть без учета причин, вызывающих это движение.
Пусть положение материальной точки задано радиусом-вектором , проведенным из некоторой неподвижной точки О выбранной системы отсчета. При движении материальной точки ее радиус-вектор меняется в общем случае как по величине, так и по направлению, то есть радиус-вектор зависит от времени t. Геометрическое место концов радиуса-вектора будет траекторией материальной точки.

3. Кинематика материальной точки.
Скорость и ускорение точки.

3. Кинематика материальной точки.
Скорость и ускорение точки.

3. Кинематика материальной точки.
Скорость и ускорение точки.
В классической механике состояние частицы или материальной точки в момент времени при координатном способе характеризуется тремя координатами и тремя компонентами скорости, причем предполагается, что все шесть величин в указанный момент можно найти на опыте с любой степенью точности.
Другим понятием, характеризующим движение точки, является ускорение. Ускорение – это физическая величина, характеризующая быстроту изменения скорости

3. Кинематика материальной точки.
Скорость и ускорение точки.

3. Кинематика материальной точки.
Скорость и ускорение точки.

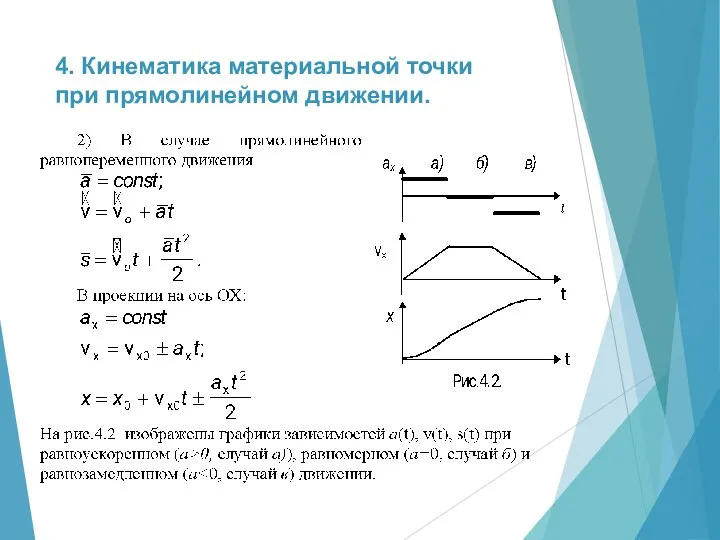
4. Кинематика материальной точки
при прямолинейном движении.
Движение, при котором траектория – прямая линия, называется прямолинейным движением. При прямолинейном движении вектор перемещения совпадает с соответствующим участком траектории и модуль перемещения равен пройденному пути, если направление движения не изменяется.

4. Кинематика материальной точки
при прямолинейном движении.

4. Кинематика материальной точки
при прямолинейном движении.

5. Криволинейное движении материальной точки.
Криволинейное движение – движение, при котором траектория – кривая линия. Если материальная точка движется по произвольной кривой, то эту кривую надо разбить на малые дуги и каждую из них совместить с дугой некоторой окружности. Каждая такая окружность называется окружностью кривизны, а радиус называется радиусом кривизны траектории в данной точке.

5. Криволинейное движении материальной точки.

5. Криволинейное движении материальной точки.
Нормальное (центростремительное) ускорение характеризует изменение скорости по направлению. Вектор нормального ускорения направлен по радиусу к центру окружности.

5. Криволинейное движении материальной точки.

5. Криволинейное движении материальной точки.

6. Вращение твердого тела вокруг неподвижной оси.
Связь между линейными и угловыми величинами.
Вращательным движением называется такое движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной прямой, называемой осью вращения.

6. Вращение твердого тела вокруг неподвижной оси.
Связь между линейными и угловыми величинами.

6. Вращение твердого тела вокруг неподвижной оси.
Связь между линейными и угловыми величинами.

6. Вращение твердого тела вокруг неподвижной оси.
Связь между линейными и угловыми величинами.

6. Вращение твердого тела вокруг неподвижной оси.
Связь между линейными и угловыми величинами.