Слайд 2Определение скорости при разных способах задания движения точки.
Векторный способ задания движения точки

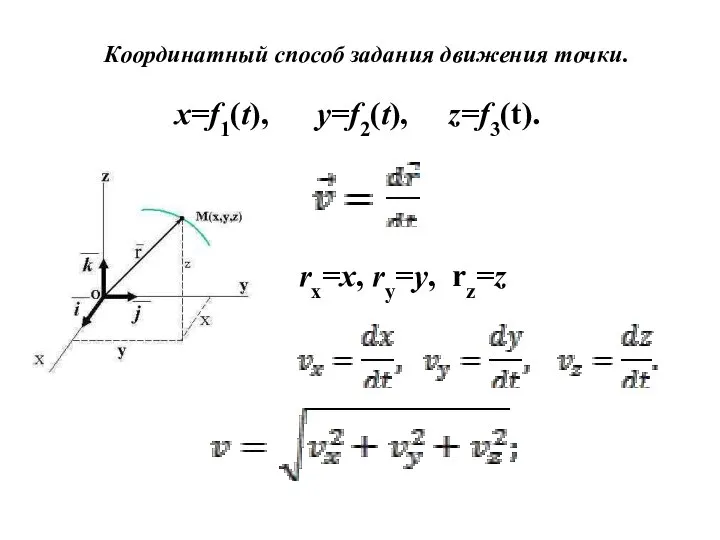
Слайд 3Координатный способ задания движения точки.
rx=x, ry=y, rz=z
x=f1(t), y=f2(t), z=f3(t).
Слайд 4Естественный способ задания движения точки
S = f(t).

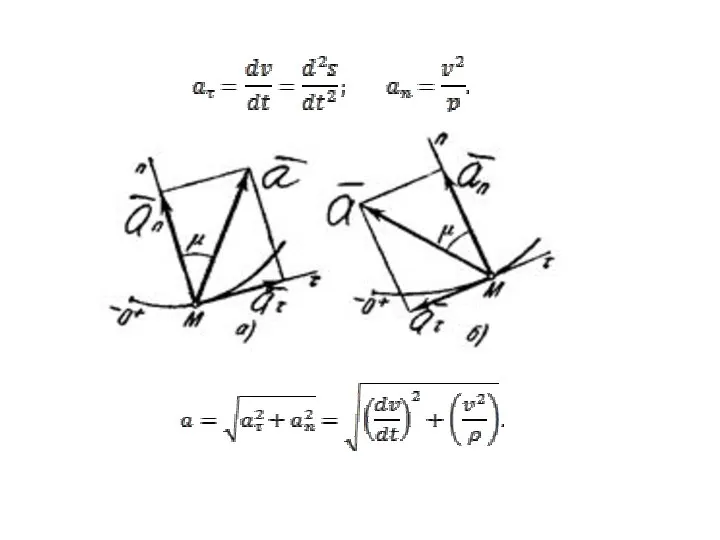
Слайд 5Определение ускорения. Касательное и нормальное ускорение точки
Векторный способ задания движения точки

Слайд 6Координатный способ задания движения точки
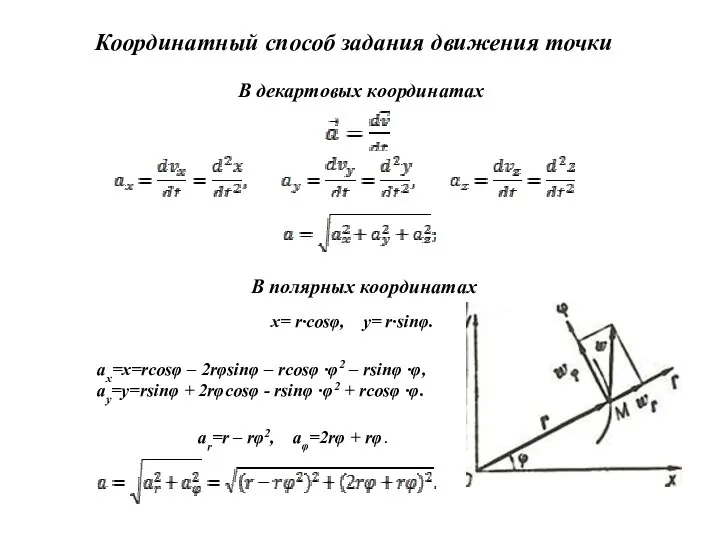
В декартовых координатах
В полярных координатах
х= r∙соsφ, у= r∙sinφ.
ax=x=rcosφ – 2rφsinφ – rcosφ ∙φ2 – rsinφ ∙φ,
ay=y=rsinφ + 2rφcosφ - rsinφ ∙φ2 + rcosφ ∙φ.
ar=r – rφ2, aφ=2rφ + rφ.
Слайд 7Естественный способ задания движения точки







 Демонтаж тормозной системы автомобиля
Демонтаж тормозной системы автомобиля Прикладная механика. Лекция №1
Прикладная механика. Лекция №1 Равновесие сил с учётом трения покоя, сцепления
Равновесие сил с учётом трения покоя, сцепления Спектры. Устройство спектроскопа
Спектры. Устройство спектроскопа Основные понятия механики
Основные понятия механики Презентация на тему Движение под действием нескольких сил
Презентация на тему Движение под действием нескольких сил  Контроль – измерительные приборы и автоматика (для операторов ТХУ)
Контроль – измерительные приборы и автоматика (для операторов ТХУ) Испарение и конденсация
Испарение и конденсация Физика твердого тела
Физика твердого тела Нейтронное излучение: опасности и перспективы
Нейтронное излучение: опасности и перспективы Типовые соединения деталей машин
Типовые соединения деталей машин Решение задач: построение изображений в линзах
Решение задач: построение изображений в линзах Types of thermometers
Types of thermometers Закон вращательного движения абсолютно твердого тела. Гироскоп
Закон вращательного движения абсолютно твердого тела. Гироскоп Презентация по физике "Атомная энергетика" -
Презентация по физике "Атомная энергетика" -  Презентация на тему Большой адронный коллайдер
Презентация на тему Большой адронный коллайдер  Переменный ток. Решение задач
Переменный ток. Решение задач Расчет неразъемных соединений
Расчет неразъемных соединений Презентация на тему Полупроводники
Презентация на тему Полупроводники  Элементарные частицы
Элементарные частицы Анализ методов повышения КПД судовой пароэнергетической установки
Анализ методов повышения КПД судовой пароэнергетической установки Ядерные реакции
Ядерные реакции Состав ядра атома. Энергия связи атомных ядер. Дефект масс
Состав ядра атома. Энергия связи атомных ядер. Дефект масс О времени и пространстве
О времени и пространстве Презентация на тему Взаимное притяжение и отталкивание молекул
Презентация на тему Взаимное притяжение и отталкивание молекул  Модели строения атома
Модели строения атома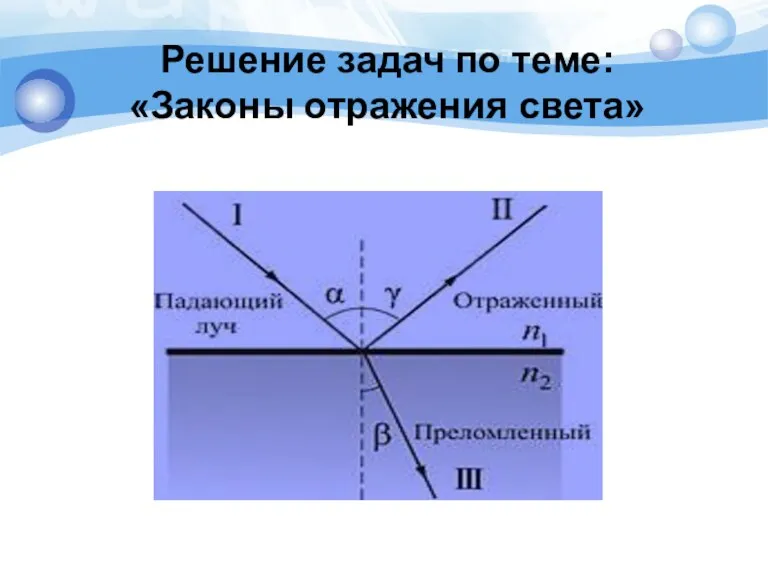 Законы отражения света. Решение задач
Законы отражения света. Решение задач Обозначение трехвинтовых насосов
Обозначение трехвинтовых насосов