Основные постулаты квантовой теории

Лекция II
Основные постулаты
Квантовой теории

Постулат - это
утверждение, обобщающее
экспериментальные факты и
не требующее дополнительного обоснования

Базовые постулаты
Что такое частица?

I. Геометрия пространства и частиц
2. Частица представляет собой точку.
Положение частицы в момент времени t
определяется координатами (x,y,z)
однозначно
Пространство является эвклидовым.
Время всюду течет одинаково в независимости от системы отсчета

I. Экспериментальные основания
На малых расстояниях , соответствующих размерам атомов эффектов кривизны не наблюдается (?!)
2. Во всех экспериментах электрон ведет себя как точка!
3. Тяжелые частицы (протоны, нейтроны) имеют внутреннюю структуру, но обнаруживают в структуре точечные объекты - партоны

Базовые постулаты
Что такое частица-волна?

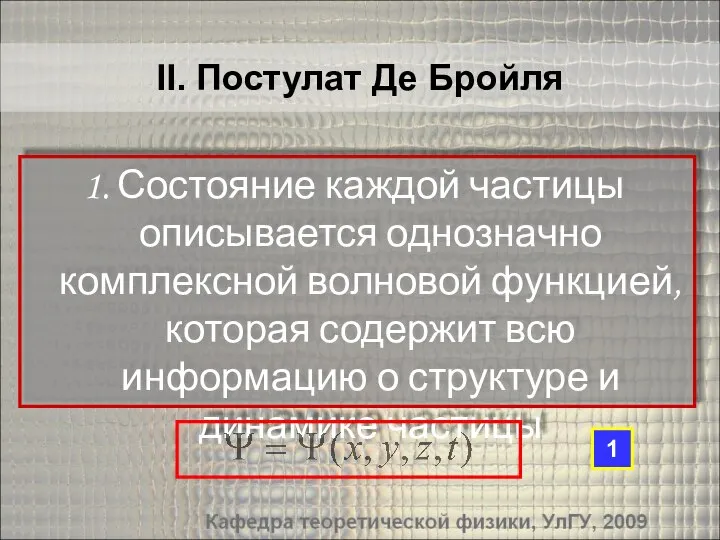
II. Постулат Де Бройля
Состояние каждой частицы описывается однозначно комплексной волновой функцией, которая содержит всю информацию о структуре и динамике частицы
1

2. Волновая функция свободной частицы
может быть представлена в виде
гармонической волны
II. Постулат Де Бройля
2

III. Статистический постулат Борна
1. Не возможно достоверно предсказать заранее (до эксперимента), где частица будет обнаружена в момент времени t.
Поэтому закономерности движения квантовых частиц и других объектов носят вероятностный характер!
Носят вероятностный характер!

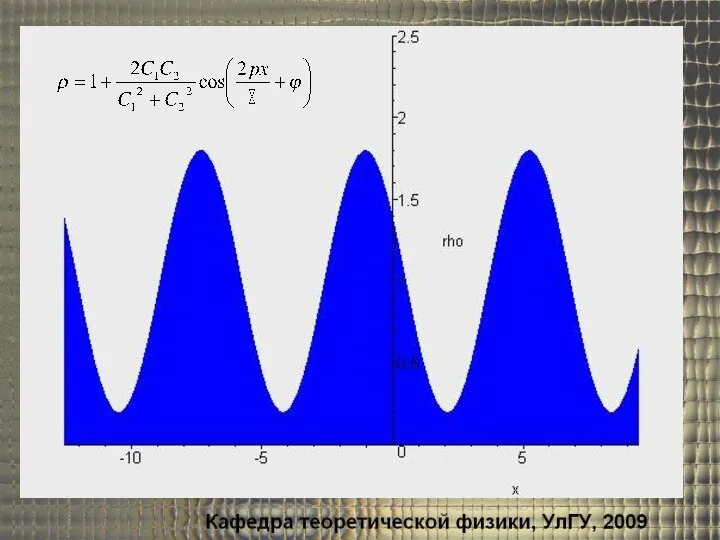
III. Статистический постулат Борна
2. Величина |Ψ(x,y,z,t)|2 представляет собой плотность вероятности обнаружить частицу в точке с координатами (x,y,z) в момент времени t
3

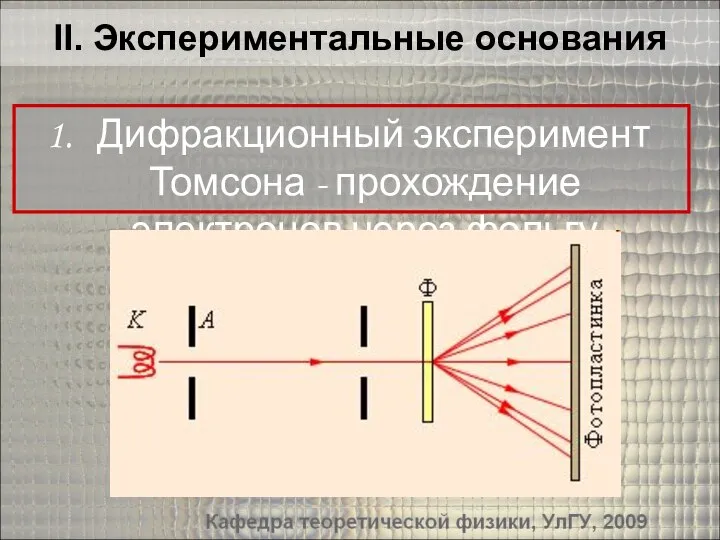
II. Экспериментальные основания
Дифракционный эксперимент Томсона - прохождение электронов через фольгу

Большая экспозиция,
b) Малая экспозиция
http://www.college.ru/physics/courses/op25part2/content/chapter5/section/

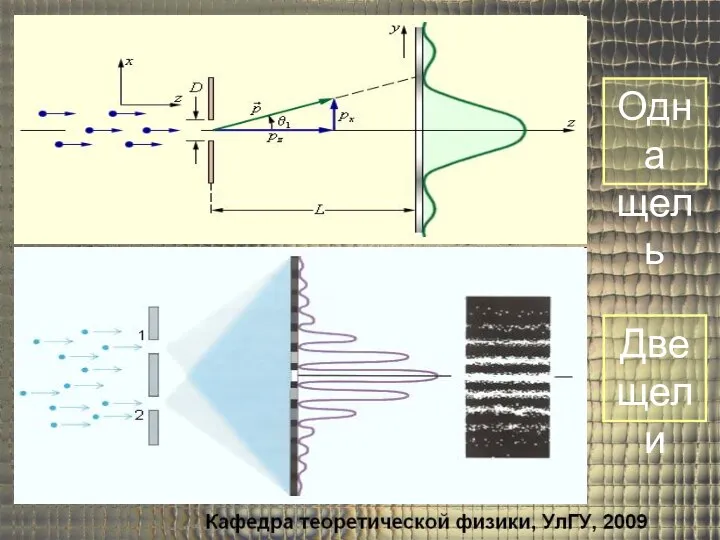
Одна щель
Две щели

Постулаты конструирования
состояний
Как вычислить волновую функцию?

I. С какой скоростью движется
частица-волна?
Фазовая скорость
волны Де Бройля

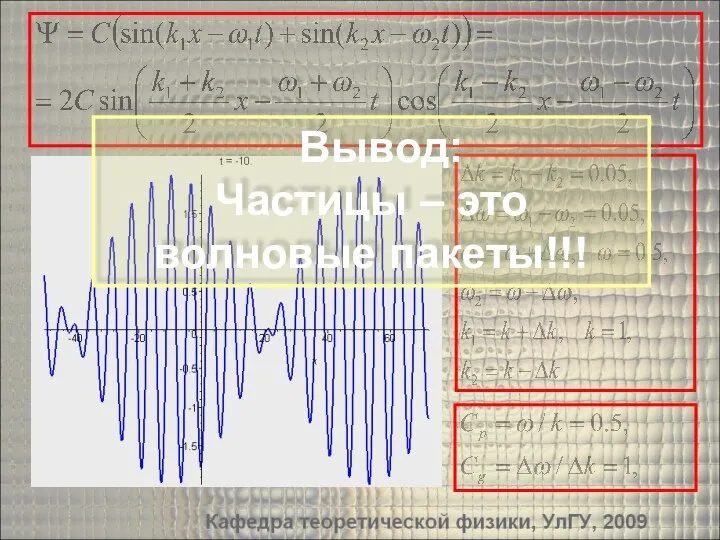
Кафедра Теоретической физик, 2009
I. С какой скоростью движется
частица-волна?
Групповая скорость
волны Де Бройля
Реальной частице необходимо сопоставлять групповую скорость волн
Де Бройля!!!
4

Вывод:
Частицы – это волновые пакеты!!!

II. Как устроен волновой пакет
частицы?
Постулат: принцип суперпозиции
Если частица в данной физической обстановке может находится в состояниях Ψ1(x,y,z,t) и Ψ2 (x,y,z,t), то она может в данной обстановке находится и в состоянии Ψ =C1Ψ1(x,y,z,t) + C2Ψ2 (x,y,z,t),
Вывод:
Волновую функцию можно собирать из отдельных “кубиков”!

Кубики для принципа суперпозиции
Или
как найти “простейшие” состояния?

I. Состояния с фиксированным
значением динамической переменной
Состоянием с фиксированным значением Q0 динамической переменной Q называется такое состояние, для которого эксперимент по измерению Q
с вероятностью 1 дает дает значение
Q=Q0

Состоянием с фиксированным значением динамической переменной Q
описывается одной волновой функцией
ΨQ(Q0,x,y,z,t).
Индекс внизу указывает имя фиксированной динамической переменной, а само значение указывается среди аргументов

Пример
Состояние с фиксированным
импульсом

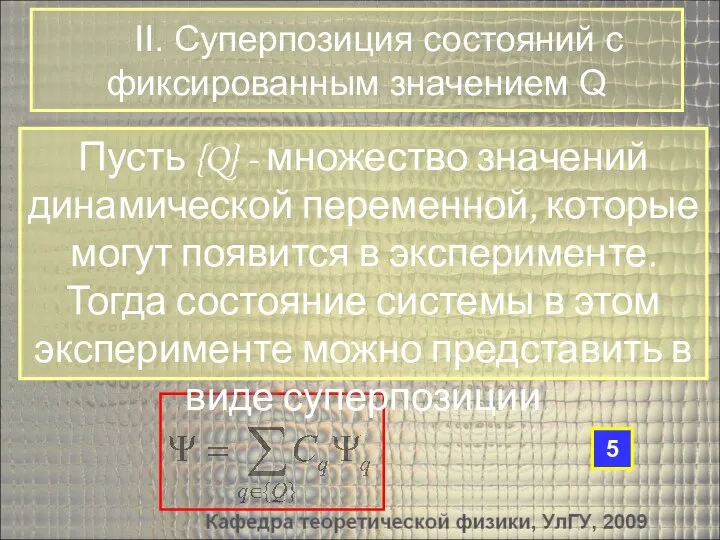
Пусть {Q} - множество значений динамической переменной, которые могут появится в эксперименте. Тогда состояние системы в этом эксперименте можно представить в виде суперпозиции
II. Суперпозиция состояний с фиксированным значением Q
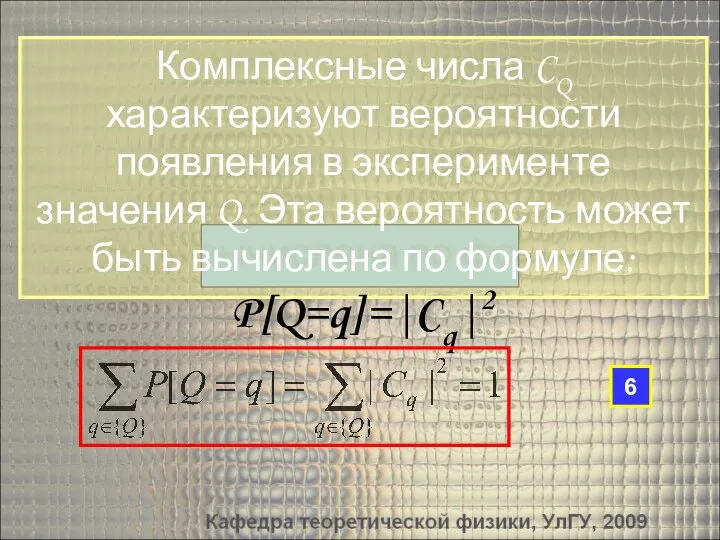
5

Комплексные числа CQ характеризуют вероятности появления в эксперименте значения Q. Эта вероятность может быть вычислена по формуле:
P[Q=q]=|Cq|2
6

III. Проекционный постулат
Сразу после эксперимента по измерению динамической переменной Q , результатом которого было значение Q0 , волновая функция системы будет иметь вид
Ψ Q(Q0 ,x,y,z,t).

Парадокс Шредингера

Эрвин Шрёдингер
Arvin Shredinger
( 12.08.1887 года - 04.01.1961 года )
Родился в Вене. В 1906 г. он поступил в Венский университет. В 1910 г.
защищает докторскую диссертацию. Во время первой мировой войны
Шрёдингер служил офицером-артиллеристом в захолустном гарнизоне,
расположенном в горах, вдали от линии фронта. По окончании войны он
возвращается во 2-й физический институт в Вене, В 1920 г. Шрёдингер
отправился в Германию, где стал ассистентом Макса Вина в Иенском
университете, но через четыре месяца становится адъюнкт-профессором
Штутгартского технического университета. Через один семестр он
покидает Штутгарт и переезжает в Швейцарию и становится преемником
Эйнштейна и Макса фон Лауэ и профессором кафедры физики Цюрихского университета. Он следит и за успехами квантовой теории, но не сосредоточивает свое внимание на этой области вплоть до 1925 г.,когда появился благоприятный отзыв Эйнштейна по поводу волновой теории материи Луи де Бройля.

В закрытый ящик помещён кот. В ящике имеется механизм, содержащий радиоактивное ядро и ёмкость с ядовитым газом. Параметры эксперимента подобраны так, что вероятность того, что ядро распадётся за 1 час, составляет 50 %. Если ядро распадается, оно приводит механизм в действие, он открывает ёмкость с газом, и кот умирает. Согласно квантовой механике, если над ядром не производится наблюдения, то его состояние описывается суперпозицией (смешением) двух состояний — распавшегося ядра и нераспавшегося ядра, следовательно, кот, сидящий в ящике, и жив, и мёртв одновременно.

Вопрос стоит так: когда система перестаёт существовать как смешение двух состояний и выбирает одно конкретное? Цель эксперимента — показать, что квантовая механика неполна без некоторых правил, которые указывают, при каких условиях происходит коллапс волновой функции и кот становится либо мёртвым, либо остаётся живым, но перестаёт быть смешением того и другого.

Состояние с фиксированным значением энергии E
в пустом одномерном пространстве описывается волновой функцией
ΨE(E0,x,y,z,t).
Пример. Суперпозиция состояний Де Бройля

Плотность вероятности не зависит от времени! Такие состояния будем называть стационарными

Состояние с фиксированным значением энергии E
в пустом трехмерном пространстве

Ортогональность состояний с фиксированным значением динамической переменной.
Поскольку результаты измерения Q со значениями q и q’(q≠q’) не совместны, то
Следовательно:

Следующая лекция
Операторное изображение динамических переменных