Содержание
- 2. Электродинамика - наука об электромагнитных полях и волнах. В ней исследуются основные закономерности, которым подчиняются электромагнитные
- 3. Понятие классической – макроскопической теории электромагнитного поля. рассматриваются процессы и поля в объемах, размеры которых несоизмеримо
- 4. Классическая теория электромагнитного поля, базируется на уравнениях Максвелла. Она охватывает широкий круг явлений, включающий современную радиоэлектронику,
- 5. 1.2. Векторные функции, характеризующие электромагнитное поле.
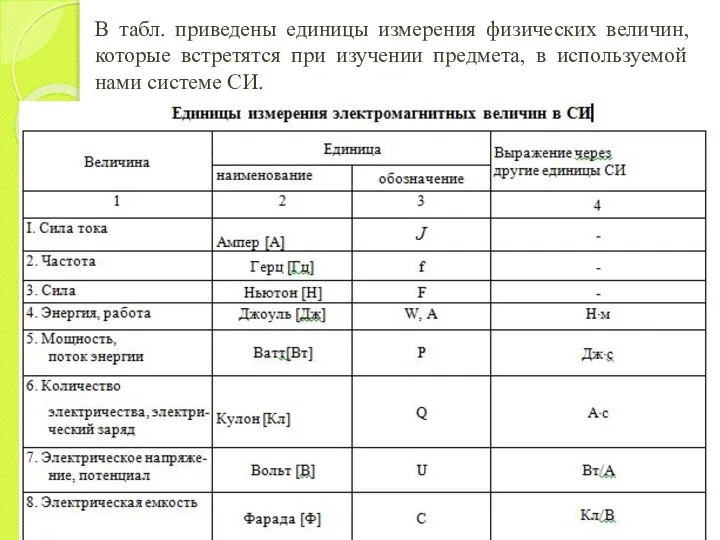
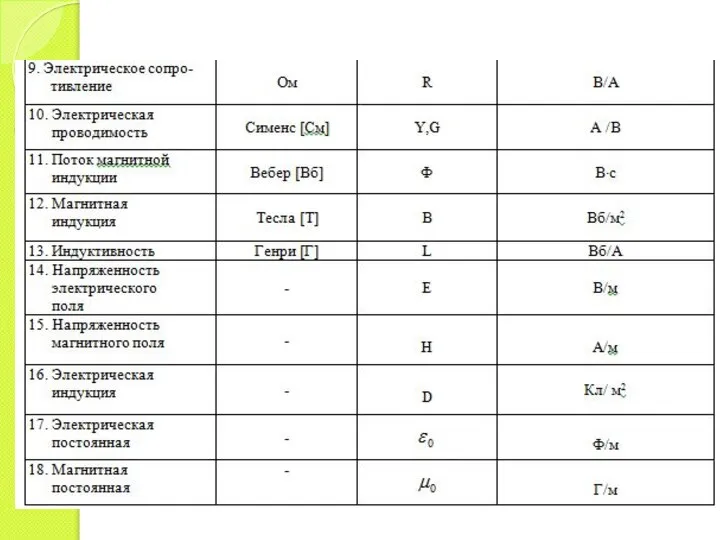
- 6. В табл. приведены единицы измерения физических величин, которые встретятся при изучении предмета, в используемой нами системе
- 8. Понятие вектора как величины, характеризуемой в отличие от скаляра не только числом, но и направлением в
- 9. 1.3. Векторы и действия над ними. Векторное сложение и вычитание производится по правилам параллелограмма и треугольника
- 10. Векторное произведение двух векторов а и b - это вектор, направленный перпендикулярно плоскости расположения перемножаемых векторов
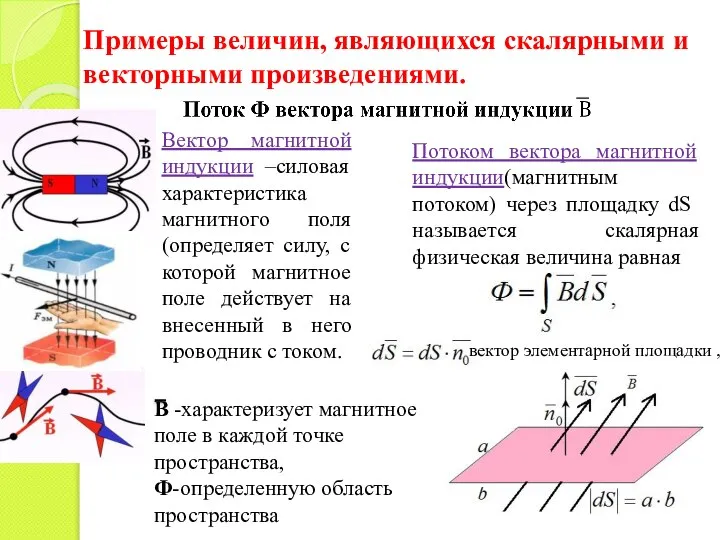
- 11. Примеры величин, являющихся скалярными и векторными произведениями. Вектор магнитной индукции –силовая характеристика магнитного поля (определяет силу,
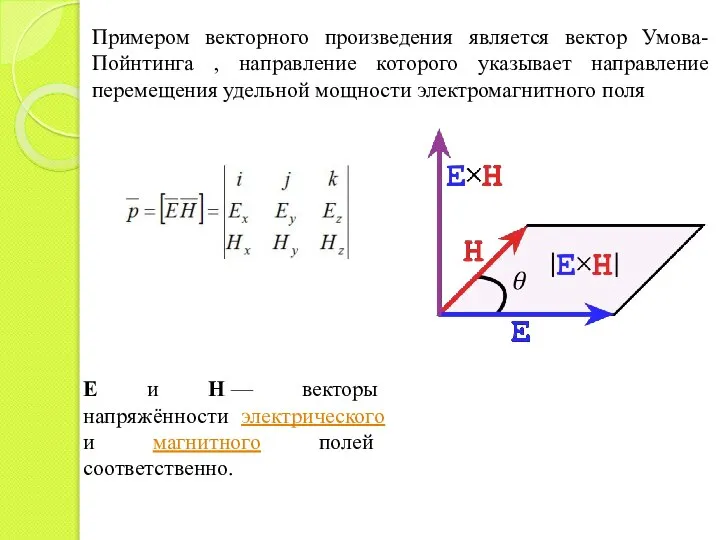
- 12. Примером векторного произведения является вектор Умова-Пойнтинга , направление которого указывает направление перемещения удельной мощности электромагнитного поля
- 13. 1.4. Поля и операции векторного анализа. Термин «поле» употребляется, когда надо сопоставить каждой точке пространства некоторую
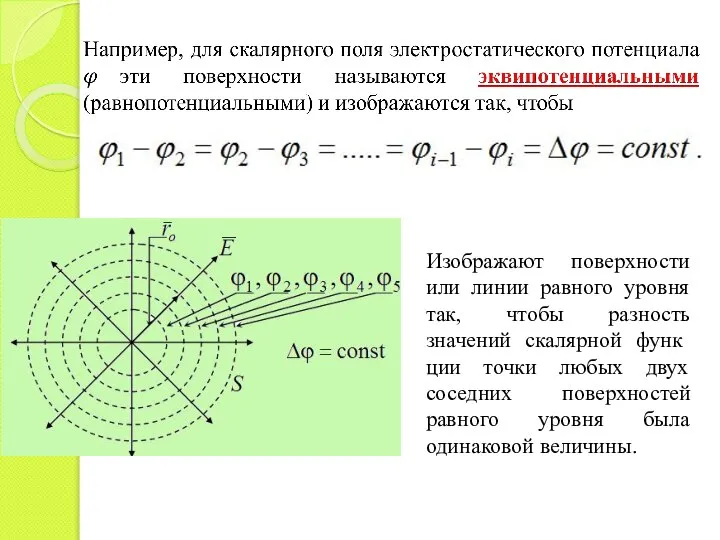
- 14. Скалярное поле графически изображается на плоскости рисунка линиями равного уровня, которые являются геометрическим местом точек равного
- 15. Изображают поверхности или линии равного уровня так, чтобы разность значений скалярной функции точки любых двух соседних
- 16. Для характеристики величины и направления скорости изменения скалярного поля в пространстве введем понятие градиента скалярного поля.
- 17. от лат. gradiens, род. падеж gradientis — шагающий, растущий) — вектор, своим направлением указывающий направление наибольшего
- 18. В декартовой системе координат градиент скалярной функции равен Мы видим, что скалярное поле φ порождает векторное
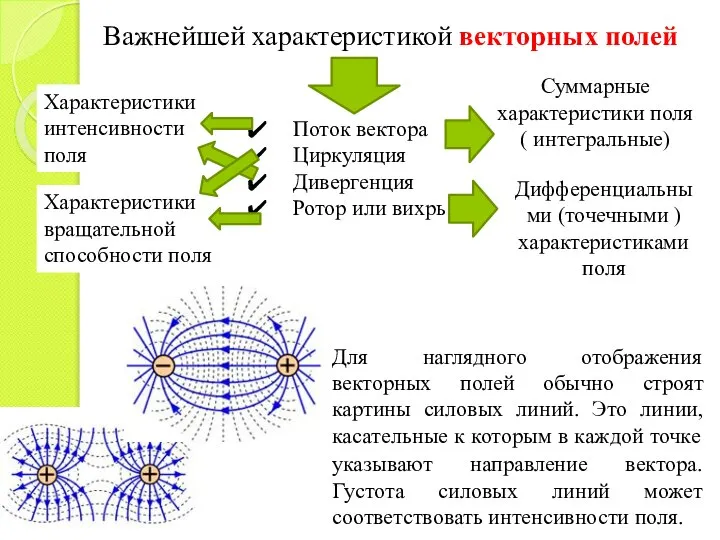
- 19. Важнейшей характеристикой векторных полей Поток вектора Циркуляция Дивергенция Ротор или вихрь Суммарные характеристики поля ( интегральные)
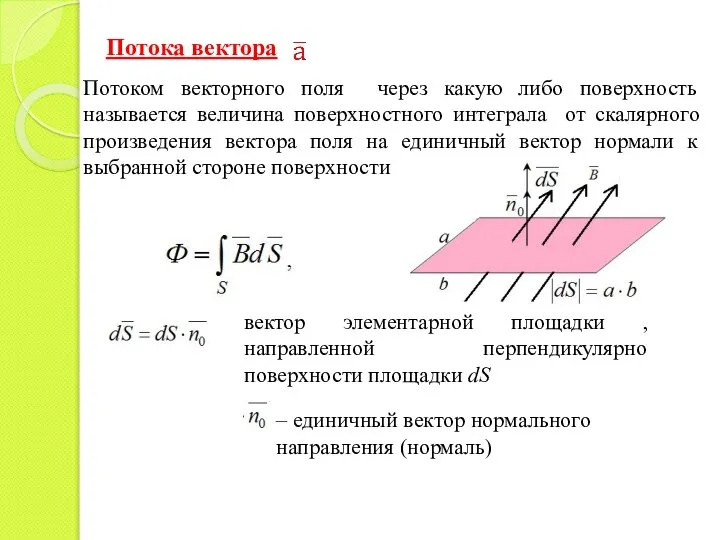
- 20. Потока вектора Потоком векторного поля через какую либо поверхность называется величина поверхностного интеграла от скалярного произведения
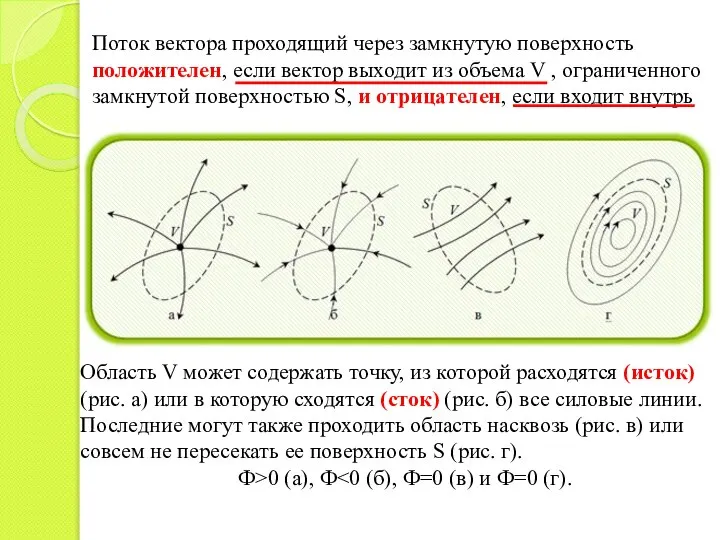
- 21. Поток вектора проходящий через замкнутую поверхность положителен, если вектор выходит из объема V , ограниченного замкнутой
- 22. С целью оценки интенсивности источников надо поток вектора а брать через достаточно малую замкнутую поверхность при
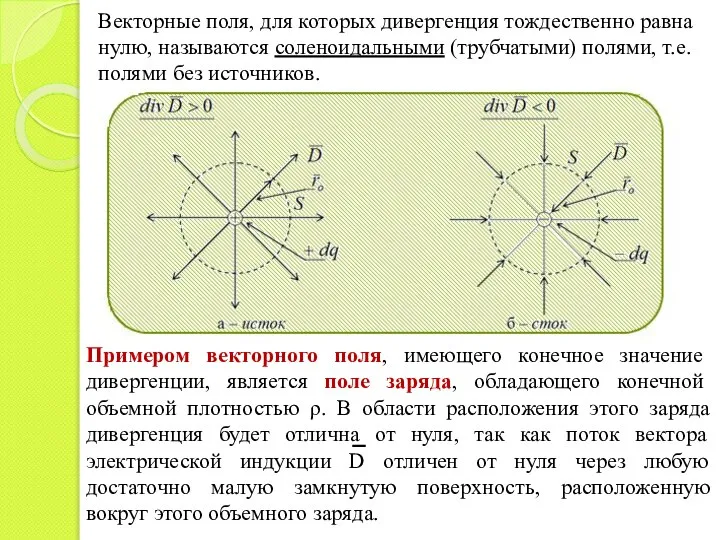
- 23. Примером векторного поля, имеющего конечное значение дивергенции, является поле заряда, обладающего конечной объемной плотностью ρ. В
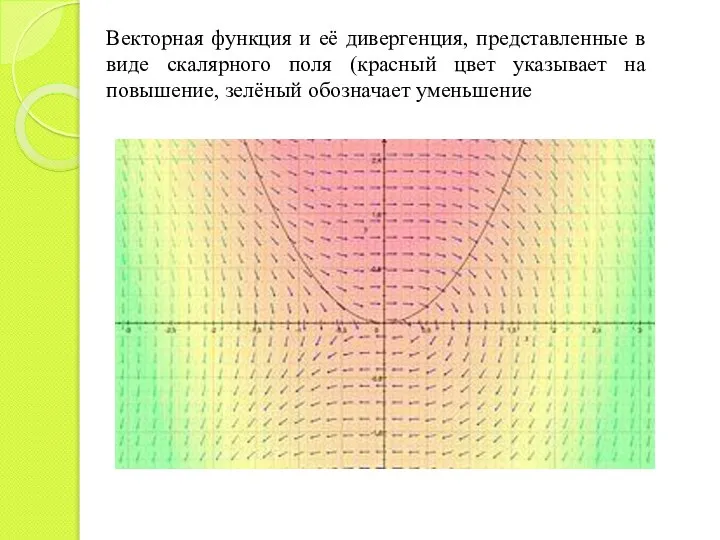
- 24. Векторная функция и её дивергенция, представленные в виде скалярного поля (красный цвет указывает на повышение, зелёный
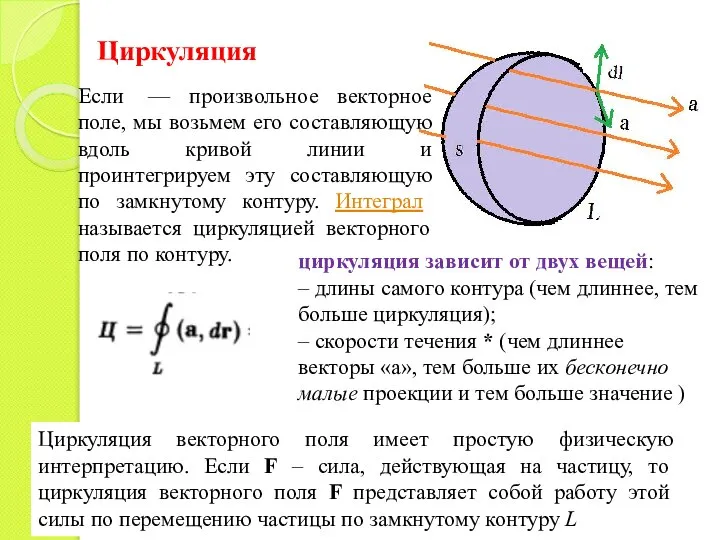
- 25. Циркуляция Циркуляция векторного поля имеет простую физическую интерпретацию. Если F – сила, действующая на частицу, то
- 26. Ротop (вихрь) вектора. указывает направление, ортогонально которому вращательная способность поля наибольшая. Ротор (вихрь) вектора является мерой
- 28. Теорема Стокса Поток ротора векторной функции а через поверхность S равен циркуляции этого вектора по контуру
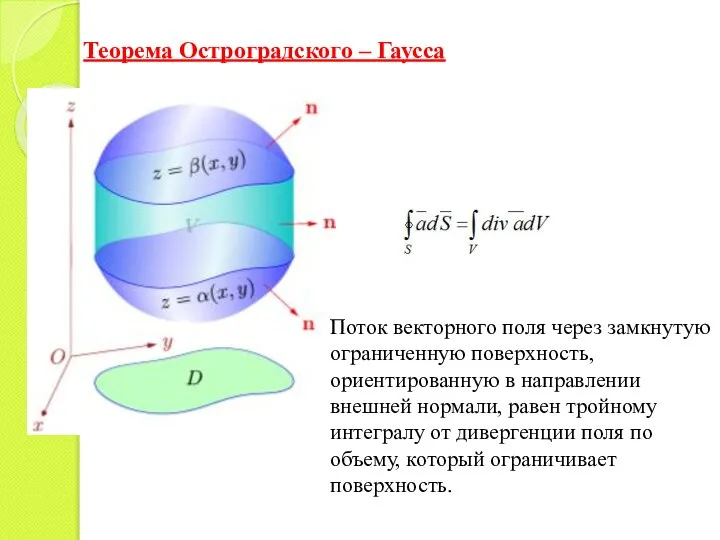
- 29. Теорема Остроградского – Гаусса Поток векторного поля через замкнутую ограниченную поверхность, ориентированную в направлении внешней нормали,
- 31. Скачать презентацию















 Сообщающиеся сосуды
Сообщающиеся сосуды Разработка стенда для исследования импульсных источников питания
Разработка стенда для исследования импульсных источников питания Механика. Введение
Механика. Введение СИЛА ТРЕНИЯ, ЕЕ РОЛЬ В ПРИРОДЕ, ТЕХНИКЕ И ПОВСЕДНЕВНОЙ ЖИЗНИ. Выполнил: Кишко А. 7 класс МКОУ Атамановской СОШ Учитель: Янюшкина
СИЛА ТРЕНИЯ, ЕЕ РОЛЬ В ПРИРОДЕ, ТЕХНИКЕ И ПОВСЕДНЕВНОЙ ЖИЗНИ. Выполнил: Кишко А. 7 класс МКОУ Атамановской СОШ Учитель: Янюшкина  Поступательное движение
Поступательное движение Относительность движения
Относительность движения Растяжение и сжатие
Растяжение и сжатие Жан Лерон Д' Аламбер. Трактат о динамике
Жан Лерон Д' Аламбер. Трактат о динамике Звук. Колебательные системы
Звук. Колебательные системы Внедрение гибридных солнечно-ветровых систем электропитания для развития ИКТ в предгорных населенных пунктах и регионах
Внедрение гибридных солнечно-ветровых систем электропитания для развития ИКТ в предгорных населенных пунктах и регионах Презентация на тему Тепловые двигатели
Презентация на тему Тепловые двигатели  Основы электричества
Основы электричества Измерительный прибор для определения влажности воздуха - гигрометр
Измерительный прибор для определения влажности воздуха - гигрометр Исследование возникновения и развития скольжения в поликристаллических образцах алюминия с помощью лазерной методики
Исследование возникновения и развития скольжения в поликристаллических образцах алюминия с помощью лазерной методики Кристаллические и аморфные тела. Механические свойства твердых тел
Кристаллические и аморфные тела. Механические свойства твердых тел В.А. Грибов. Я сдам ЕГЭ. Физика
В.А. Грибов. Я сдам ЕГЭ. Физика Гальванічні реакції
Гальванічні реакції Ядерные реакции. Атом, атомное ядро, атомная энергия (Лекция 2)
Ядерные реакции. Атом, атомное ядро, атомная энергия (Лекция 2) Теоретическая механика. Задачи
Теоретическая механика. Задачи Кинематика твердого тела/ Простейшие движения твердого тела
Кинематика твердого тела/ Простейшие движения твердого тела Компенсация реактивной мощности
Компенсация реактивной мощности Исследование процесса образования ядер капель и кристаллов в атмосфере. Лабораторная работа №2
Исследование процесса образования ядер капель и кристаллов в атмосфере. Лабораторная работа №2 Перемещение при прямолинейном равноускоренном движении (9 класс)
Перемещение при прямолинейном равноускоренном движении (9 класс) Действие жидкости на погруженное в нее тело. Сила Архимеда
Действие жидкости на погруженное в нее тело. Сила Архимеда Розв'язування задач на тему Закони вiдбивання свiтла
Розв'язування задач на тему Закони вiдбивання свiтла Дала,прерия
Дала,прерия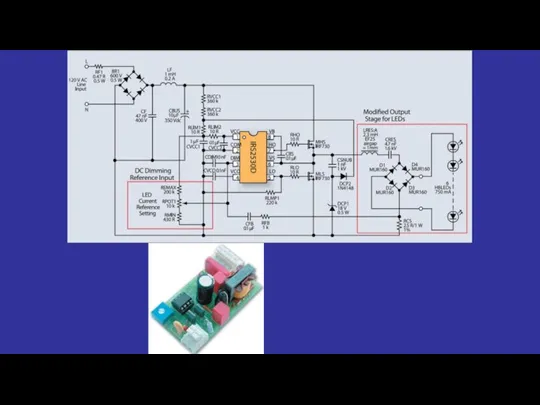 Сравнение основных параметров импульсных и линейных источников питания
Сравнение основных параметров импульсных и линейных источников питания Посадочный размер блока. Диаметр ТЭНа
Посадочный размер блока. Диаметр ТЭНа