Порядок решения задач по динамике МТ

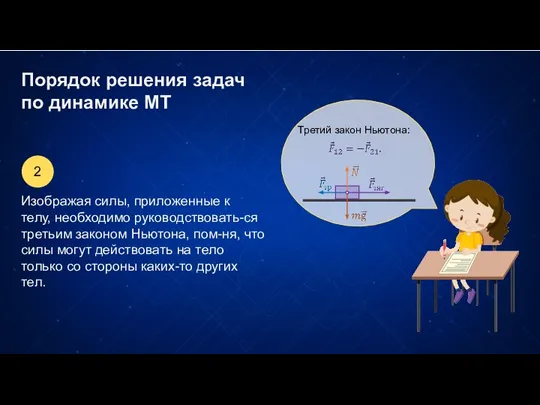
Порядок решения задач по динамике МТ
Третий закон Ньютона:

Порядок решения задач по динамике МТ
Второй закон Ньютона:

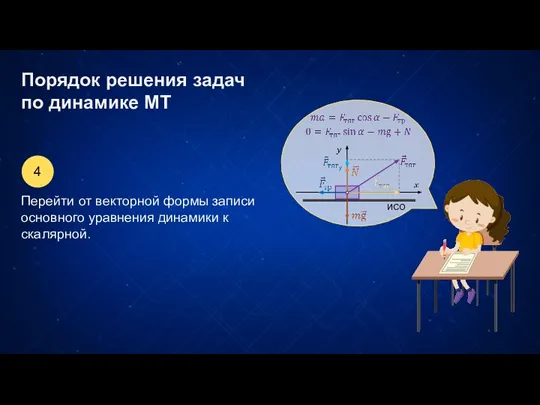
Порядок решения задач по динамике МТ
ИСО

Методы решения задач по динамике МТ
Проекция вектора на ось —
это длина отрезка между проекциями начала и конца вектора на эту ось, взятая со знаком «+» или «−».

Порядок решения задач по динамике МТ
ИСО

Порядок решения задач по динамике МТ

Порядок решения задач по динамике МТ
Т. к. тела связаны неве-сомой и нерастяжимой нитью, то

Порядок решения задач по динамике МТ
Т. к. тела связаны неве-сомой и нерастяжимой нитью, то

Порядок решения задач по динамике МТ
Т. к. тела связаны неве-сомой и нерастяжимой нитью, то

Каждая задача требует индивидуального творческого подхода и глубоких знаний теории.

Задача 1. Два груза массами 5 и 2 кг связаны невесомой нерастяжимой нитью, переброшенной через невесомый блок, который прикреплён к вершине призмы, и могут скользить по граням этой призмы. Определите ускорение грузов, если начальные скорости грузов равны нулю,
α = 60о, β = 30о, а коэффициент трения равен 0,3.
ДАНО
РЕШЕНИЕ
α
β
α
β
α
β
Второй закон Ньютона:
Закон Кулона — Амонтона:

Задача 1. Два груза массами 5 и 2 кг связаны невесомой нерастяжимой нитью, переброшенной через невесомый блок, который прикреплён к вершине призмы, и могут скользить по граням этой призмы. Определите ускорение грузов, если начальные скорости грузов равны нулю,
α = 60о, β = 30о, а коэффициент трения равен 0,3.
ДАНО
РЕШЕНИЕ
Второй закон Ньютона:
Закон Кулона — Амонтона:
α
β
α
β
α
β
Так как нить и блок невесомы, то
Так как нить нерастяжима и в блоке нет сил трения, то
Ускорение грузов:

Задача 1. Два груза массами 5 и 2 кг связаны невесомой нерастяжимой нитью, переброшенной через невесомый блок, который прикреплён к вершине призмы, и могут скользить по граням этой призмы. Определите ускорение грузов, если начальные скорости грузов равны нулю,
α = 60о, β = 30о, а коэффициент трения равен 0,3.
ДАНО
РЕШЕНИЕ
Второй закон Ньютона:
α
β
α
β
α
β
Так как нить и блок невесомы, то
Так как нить нерастяжима и в блоке нет сил трения, то
Ускорение грузов:
ОТВЕТ: система грузов движется с ускорением 3 м/с2.

Порядок решения задач по динамике МТ
или

Задача 2. Определите угол наклона к вертикали нити математического маятника, если точка подвеса маятника жёстко прикреплена к потолку вагона, движущегося с ускорением 5 м/с2 относительно Земли.
ДАНО
РЕШЕНИЕ
Второй закон Ньютона в проекциях на координатные оси:
Угол наклона нити:
ОТВЕТ: угол наклона к вертикали нити математического маятника равен 63о.