Potential Flow Theory

Elementary fascination Functions
To Create IRROTATIONAL PLANE FLOWS
The uniform flow
The source and the sink
The vortex

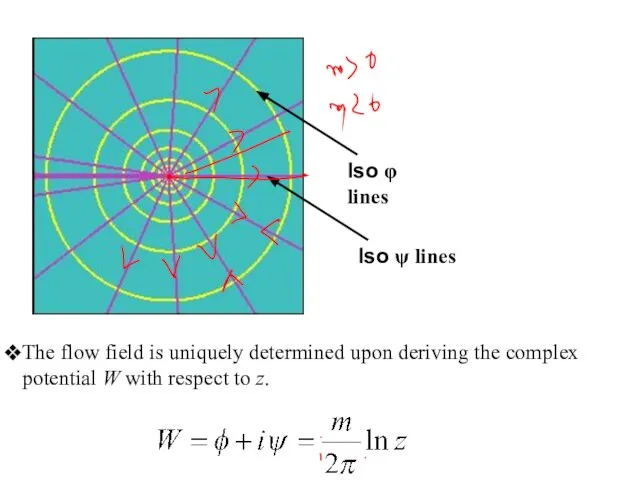
THE SOURCE OR SINK
source (or sink), the complex potential of which is
This is a pure radial flow, in which all the streamlines converge at the origin, where there is a singularity due to the fact that continuity can not be satisfied.
At the origin there is a source, m > 0 or sink, m < 0 of fluid.
Traversing any closed line that does not include the origin, the mass flux (and then the discharge) is always zero.
On the contrary, following any closed line that includes the origin the discharge is always nonzero and equal to m.

The flow field is uniquely determined upon deriving the complex potential W with respect to z.
Iso ψ lines
Iso φ lines

A Combination of Source & Sink

THE DOUBLET
The complex potential of a doublet

Uniform Flow Past A Doublet
The superposition of a doublet and a uniform flow gives the complex potential

Find out a stream line corresponding to a value of steam function is zero

There exist a circular stream line of radium R, on which value of stream function is zero.
Any stream function of zero value is an impermeable solid wall.
Plot shapes of iso-streamlines.

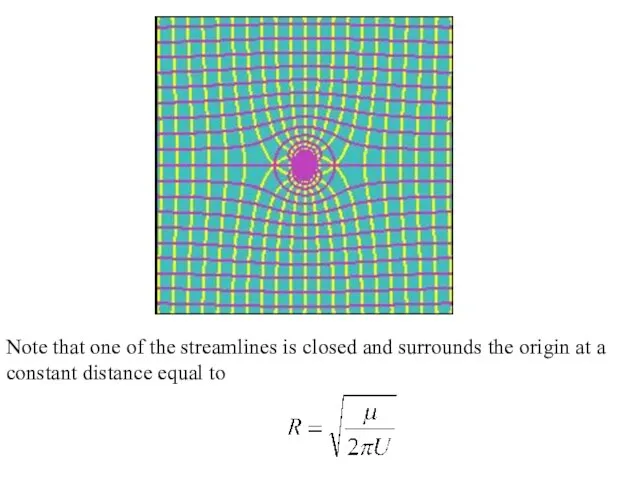
Note that one of the streamlines is closed and surrounds the origin at a constant distance equal to

Recalling the fact that, by definition, a streamline cannot be crossed by the fluid, this complex potential represents the irrotational flow around a cylinder of radius R approached by a uniform flow with velocity U.
Moving away from the body, the effect of the doublet decreases so that far from the cylinder we find, as expected, the undisturbed uniform flow.
In the two intersections of the x-axis with the cylinder, the velocity will be found to be zero.
These two points are thus called stagnation points.

To obtain the velocity field, calculate dw/dz.

Equation of zero stream line:

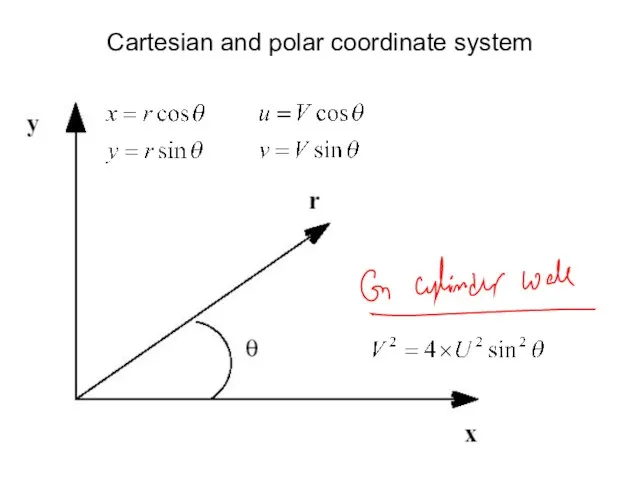
Cartesian and polar coordinate system

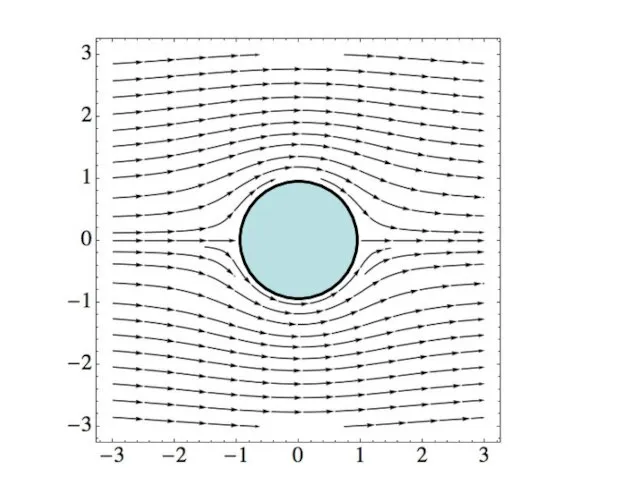
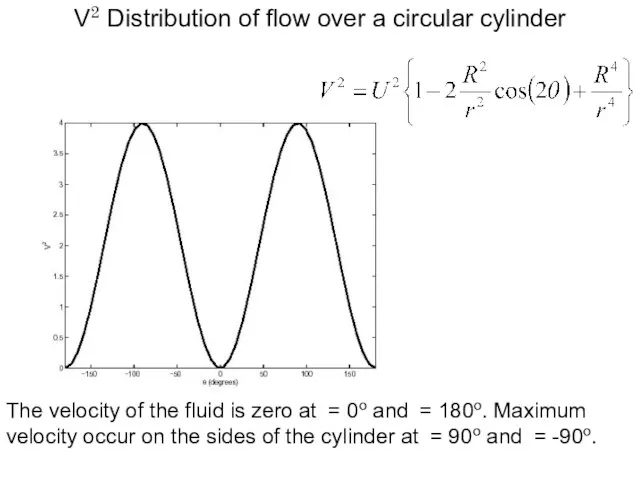
V2 Distribution of flow over a circular cylinder
The velocity of the fluid is zero at = 0o and = 180o. Maximum velocity occur on the sides of the cylinder at = 90o and = -90o.

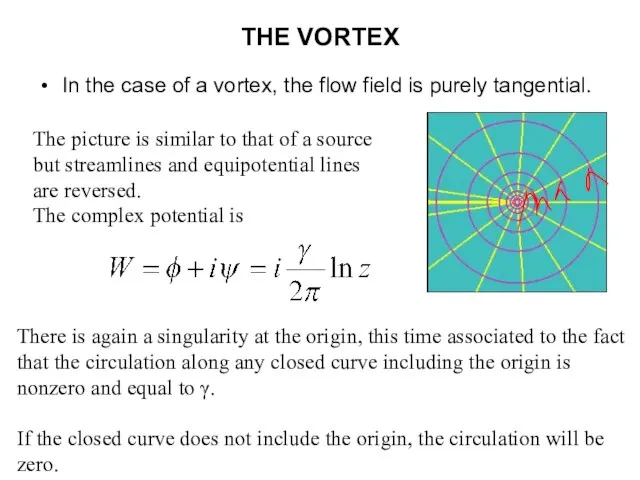
THE VORTEX
In the case of a vortex, the flow field is purely tangential.
The picture is similar to that of a source but streamlines and equipotential lines are reversed.
The complex potential is
There is again a singularity at the origin, this time associated to the fact that the circulation along any closed curve including the origin is nonzero and equal to γ.
If the closed curve does not include the origin, the circulation will be zero.

Uniform Flow Past A Doublet with Vortex
The superposition of a doublet and a uniform flow gives the complex potential

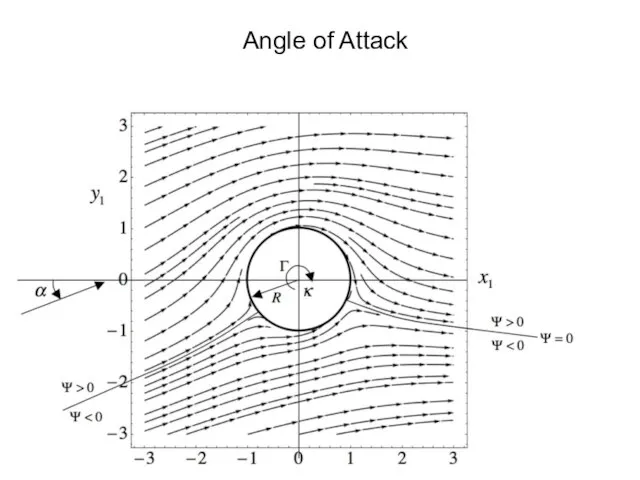
Angle of Attack

The Natural Genius
&
The Art of Generating Lift

Hydrodynamics of Prey & Predators

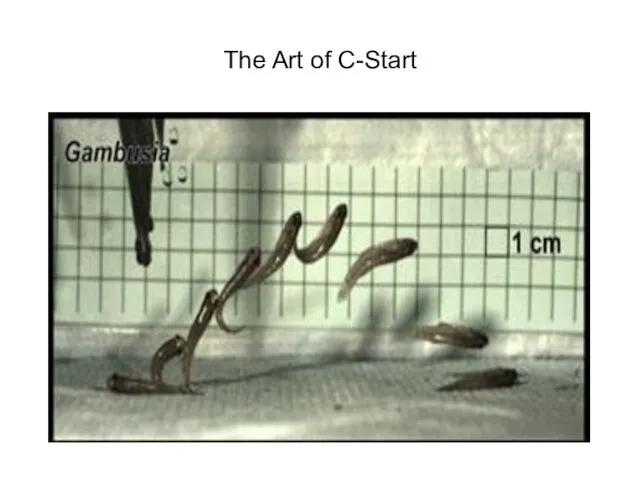
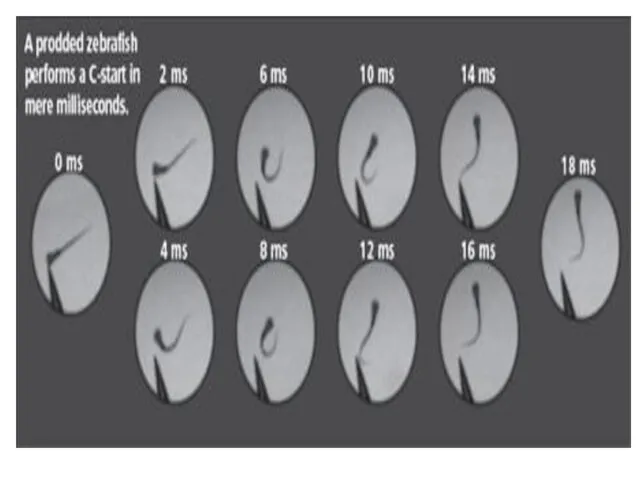
The Art of C-Start

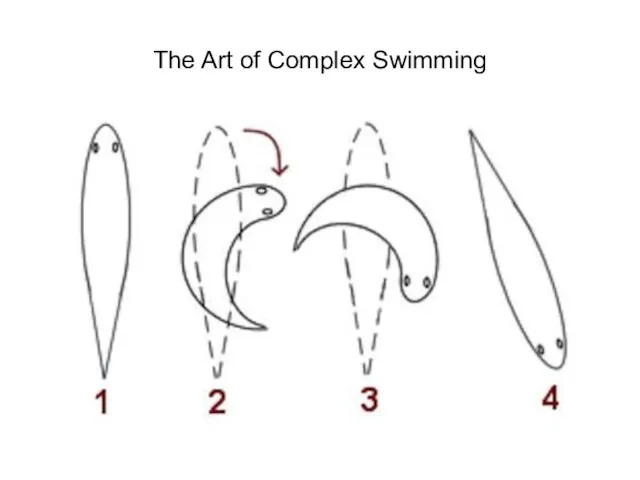
The Art of Complex Swimming

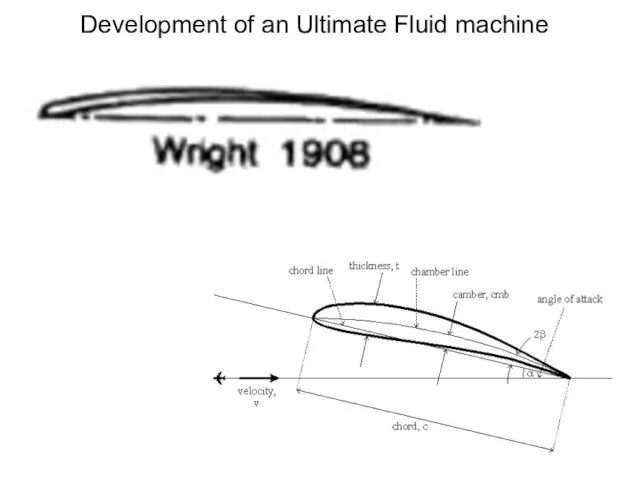
Development of an Ultimate Fluid machine

The Art of Transformation
Our goal is to map the flow past a cylinder to flow around a device which can generate an Upwash on existing Fluid.
There are several free parameters that can be used to choose the shape of the new device.
First we will itemize the steps in the mapping:

Transformation for Inventing a Machine
A large amount of airfoil theory has been developed by distorting flow around a cylinder to flow around an airfoil.
The essential feature of the distortion is that the potential flow being distorted ends up also as potential flow.
The most common Conformal transformation is the Jowkowski transformation which is given by
To see how this transformation changes flow pattern in the z (or x - y) plane, substitute z = x + iy into the expression above to get